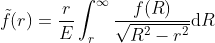Module for computing the Wicksell transform of continuous distributions.
Project description
Wicksell-py
A Python class for computing Wicksell's transforms of continuous distributions.
Purpose
Consider a medium consisting in a large number of spheres whose radii follow a Probability Density Function (PDF) f. If sections of the medium are made at random lattitudes, the radius of apparent disks (denoted r below) would follow the PDF [1]:
where E is the mean value of f. The previous formula is refered to as the Wicksell's equation.
The aim of this project is to provide a robust and convinient way to compute the statistics of apparents disks (related to values of r). It is based on histogram decomposition of f, as detailed in [2].
Installation and use
First, add the file wicksell_transform.py to your working Python directory. Then, just import the wicksell_trans class
from wicksell_transform import wicksell_trans
and create an instance of that class, passing the underlying distribution (that used for computing the Wicksell transform).
wt = wicksell_trans(distro)
In the example above, distro must be a continuous distribution, as defined in the scipy's stats module. Finally, use this instance as a usual scipy's distribution. All the parameters related to the underlying distribution are inferred to the transformed one. The loc and scale parameters of the underlying distribution are renamed baseloc and basescale, respectivelly.
Example
In the following, the lognormal distribion is considered.
import scipy.stats as stats
import numpy as np
from wicksell_transform import wicksell_trans
wlognorm = wicksell_trans(stats.lognorm)
s = 0.1 # Shape parameter for lognormal
mu = 0.5
baseloc = 0
basescale = np.exp(mu) # loc parameter of underlying distribution
Compute the transformed PDF/CDF
x = np.linspace(0, 3, 1000)
pdf = wlognorm.pdf(x, s, baseloc, basescale)
cdf = wlognorm.cdf(x, s, baseloc, basescale)
Generate random variables
data = wlognorm.rvs(s, baseloc, basescale, size=1000, random_state=0)
The random state is fixed here for reproductibility.
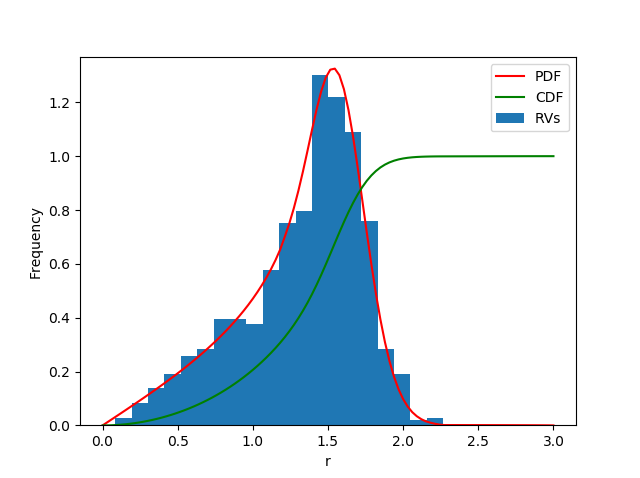
Plot results
from matplotlib import pyplot as plt
fig, ax1 = plt.subplots()
ax1.hist(data, bins=20, density=True, label='RVs')
ax1.set_ylim(bottom=0.0)
ax1.plot(x, pdf, 'r', label='PDF')
ax1.plot(x, cdf, 'g', label='CDF')
ax1.set_ylim(bottom=0.0)
ax1.legend()
ax1.set_xlabel('r')
ax1.set_ylabel('Frequency')
plt.show()
Fit the empirical data
Empirical data can be used to fit the distribution in odrer to get the optimal distribution parameters:
theta = wlognorm.fit(data, fbaseloc=0.0)
Here, the fit is made assuming that the location parameter is 0 (as a reminder, this parameter has been renamed baseloc). The fit method is a build-in method provided in all rv_continuous distributions. See the related documentation for details.
The example below roughly leads to:
(0.10258798884347263, 0.0, 1.649539304907202, 0.0, 1.0)
It appears that the first parameter is close to s (0.1) whereas the basescale (3rd one) corresponds to µ=ln(1.654)=0.5005 (instead of 0.5). Note that the 2 last arguments relate to the location and scale parameters of the transformed distribution. Thus, they are not relevant at all.
Perform a goodness of fit test
The transformed CDF can be used to perform the Kolmogorov-Smirnov test. For instance, the parameters evaluated by fitting lead to:
stats.kstest(data, wlognorm.cdf, theta)
KstestResult(statistic=0.020989374537414673, pvalue=0.7704283648898784)
:warning: Caveat :warning:
Using the histogram decomposition instead of computing the improper integral considerably speeds up the computation of the PDF/CDF. Still, it can be time consuming. Thus the fit method can be slow. Indeed, the example above takes about 100 seconds to complete on an Intel i9 @ 2.30 GHz.
Cite this work
If you use this tool in your research, please cite reference [2].
References
[1] Wicksell, S. D. (1925). The corpuscle problem: A mathematical study of a biometric problem. Biometrika, 17(1/2):84–99, DOI: 10.2307/2332027
[2] Depriester, D. and Kubler, R. (2021). Grain size estimation in polycrystals: solving the corpuscle problem using Maximum Likelihood Estimation. Journal of Structural Geology, 151:104418, ISSN 0191-8141, DOI: 10.1016/j.jsg.2021.104418
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file Wicksell-1.0.0.tar.gz.
File metadata
- Download URL: Wicksell-1.0.0.tar.gz
- Upload date:
- Size: 6.6 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.9.15
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 9a20c6ac1dba81a950988dda9fc432c5385becae89e5989829a8fdaed452a496 |
|
| MD5 | 4d022555fbd57cc70930358b036e0120 |
|
| BLAKE2b-256 | 7f264aa558aa68da9a4d6db0aeb2c35ff133a66d1c1b77504d1b31c70ea029d5 |
File details
Details for the file Wicksell-1.0.0-py3-none-any.whl.
File metadata
- Download URL: Wicksell-1.0.0-py3-none-any.whl
- Upload date:
- Size: 6.9 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.9.15
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | c0ba5169847f084c8265e56b7d288c2b03e0b00659b33e11ec77821f468a04dd |
|
| MD5 | 6df393623a691712d75b3d4011922457 |
|
| BLAKE2b-256 | 64599ba9fecad8da9a50566bde70209616b2b8c3fdab9717730214e16ba76082 |