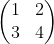Vector library

Project description

Быстрая библиотека векторной алгебры

Данная библиотека реализует основные структуры данных и их алгоритмы для векторной алгебры как для двухмерной, так и для трёхмерной. Написана на cython, поэтому быстрая. Легко установить и легко использовать.

Установка

Установить/переустановить последнюю версию можно, выполнив команду:

pip install easyvec --upgrade

2d библиотека

Представлены следующие классы, описывающие основные структуры 2d векторной алгебры:

2d структура	easyvec-класс
Вектор/точка	`Vec2`
Матрица 2х2	`Mat2`
Прямоугольник AABB	`Rect`
Полигон/полилиния	`PolyLine`

А также ряд дополнительных функций и алгоритмов для их работы с отрезками, лучами, линиями и другими примитивами

Вектор/точка `Vec2`

Поля объекта $$ \left(\begin{array}{cc} x \ y \end{array}\right) $$ Пример импорта и создания

from easyvec import Vec2

v1 = Vec2(1,2)
v2 = Vec2.from_list([1,2])
v3 = Vec2.from_list([0,-100,1,2,100], start_ind=2)
v4 = Vec2.from_dict({'x':1, 'y': 2})
v5 = Vec2.from_dict({'x':1, 'y': 2, 'some': 'data'})
v6 = Vec2(100,200) / 100
v7 = Vec2(100,200) - (99,198)
v8 = Vec2(0,1) + 1

# все эти вектора одинаковы и равны Vec2(1,2)

Доступ к полям объекта:

v1 = Vec2(1,2)
print(v1)            # (1.00, 2.00)
print(repr(v1))      # Vec2(1.0, 2.0)
print(v1.x)          # 1.0
print(v1.y)          # 2.0
print(v1[0])         # 1.0
print(v1[1])         # 2.0
print(v1['x'])       # 1.0
print(v1['y'])       # 2.0
print(v1.as_np())    # [1. 2.]
print(v1.as_tuple()) # (1.0, 2.0)
print(v1.to_dict())  # {'x': 1.0, 'y': 2.0}

x, y = v1
print(x, y)          # 1.0 2.0

for a in v1:
    print(a)         # 1.0
                     # 2.0

def foo(x, y):
    print(x, y)

foo(*v1)             # 1.0 2.0
foo(**v1)            # 1.0 2.0

Вектора можно сладывать/умножать/вычитать/делить/сравнивать/и т.п. друг с другом, со списками/кортежами/numpy-массивами и обычными числами:

v1 = Vec2(1,2)
v2 = -v1*10 + 20 
print(v2 == (10,0)) # True

v1 += 3
print(v1 != [4,5]) # False

Что касается специфических векторных операций:

v1 = Vec2(1,2)
v2 = Vec2(3,4)
print(v1.dot(v2))          # 11.0 - скалярное произведение
print(v1*v2))              # 11.0 - тоже скалярное произведение
print(v1.cross(v2))        # -2.0 - векторное произведение
print(v1 & v2)             # -2.0 - тоже векторное произведение
print(v1.norm())           # (0.45, 0.89) - единичный вектор
print(v1.norm().len())     # 1.0 - длина единичного вектора
print(v1.rotate(3.14/2))   # (-2.00, 1.00) - поворот вектора на 90 градусов
print(v1.rotate(90, degrees=True))   # (-2.00, 1.00) - поворот вектора на 90 градусов тоже
print(v1.angle_to(v2, degrees=True)) # -10.30... угол между векторами

Матрица 2х2 `Mat2`

Класс представляющий матрицу 2х2. Служит для афинных преобразований векторов Vec2

Поля объекта соответствуют положениям элементов: $$ \left(\begin{array}{cc} m11 & m12\ m21 & m22 \end{array}\right) $$

Примеры импорта и создания матрицы

$$ \left(\begin{array}{cc} 1 & 2\ 3 & 4 \end{array}\right) $$

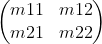
from easyvec import Mat2

m1 = Mat2(1,2,3,4)
m2 = Mat2((1,2),(3,4))
m3 = Mat2(Vec2(1,2), Vec2(3,4))
m4 = Mat2(Vec2(1,2),(3,4))
m5 = Mat2(-1,-2,-3,-4) + 2 * Mat2(1,2,3,4) 
m6 = Mat2([[1.0, 2.0], [3.0, 4.0]])

# все эти матрицы одинаковы и равны Mat2([[1.0, 2.0], [3.0, 4.0]])

Доступ к полям объекта:

mat = Mat2(1,2,3,4)
print(mat)         # [[1.00, 2.00], [3.00, 4.00]]                           
print(repr(mat))    # Mat2([[1.0, 2.0], [3.0, 4.0]])
print(mat.m11, mat.m12, mat.m21, mat.m22) # 1.0 2.0 3.0 4.0
print(mat['m11'], mat['m12'], mat['m21'], mat['m22']) # 1.0 2.0 3.0 4.0
print(mat[0][1], mat[0][1], mat[1][0], mat[1][1]) # 1.0 2.0 3.0 4.0
print(mat[0,1], mat[0,1], mat[1,0], mat[1,1]) # 1.0 2.0 3.0 4.0
print(mat.T) # [[1.00, 3.00], [2.00, 4.00]]   - транспонированная матрица
print(mat.det()) # определитель матрицы
print(mat._1 * mat == Mat2.eye()) # True - обратная матрица помноженная на исходную равняется единичной

Специфический конструктор для матрицы поворота:

from easyvec import Mat2, Vec2

m = Mat2.from_angle(90, degrees=True)
v = Vec2(1,2)

# Применяем преобразование к вектору (поворачиваем его на 90 градусов против часовой стрелки)
print(m * v)     # (2.00, -1.00)
print(m * (1,2)) # (2.00, -1.00)

Прямоугольник со сторонами, параллельными осям координат `Rect`

Содержит 4 поля с float числами: x1, y1, x2, y2. Причем точка (x1, y1) - нижняя-левая, (x2, y2) - верхняя правая

Примеры импорта и создания:

from easyvec import Rect, Vec2

r1 = Rect(1, 2, 3, 4)
r2 = Rect([1, 2], [3, 4])
r3 = Rect([1,2,3,4])
r4 = Rect(Vec2(1,2), Vec2(3,4))
r5 = Rect.from_dict({'x1': 1, 'y1': 2, 'x2': 3, 'x3': 4})

# все эти прямоугольники одинаковы и равны Rect(1.00, 2.00, 3.00, 4.00)

Также имеет специальный конструктор:

# Создает прямоугольник, описанный вокруг множества точек
r1 = Rect.bbox((1,2), (3,4), (1.5, 3)) 
r2 = Rect.bbox(Vec2(1,2), Vec2(3,4), Vec2(1.5, 3))
r3 = Rect.bbox([(1,4), Vec2(3,4), (1.5, 2)])

# все эти прямоугольники одинаковы и равны Rect(1.00, 2.00, 3.00, 4.00)

Доступ к полям объекта:

r = Rect(1,2,3,4)
print(r)          # Rect(1.00, 2.00, 3.00, 4.00)                       
print(repr(r))    # Rect(1.00, 2.00, 3.00, 4.00)
print(r.x1, r.y1, r.x2, r.y2) # 1.0 2.0 3.0 4.0
print(r['x1'], r['y1'], r['x2'], r['y2']) # 1.0 2.0 3.0 4.0
print(r[0], r[1], r[2], r[3]) # 1.0 2.0 3.0 4.0

Поддерживает операции пересечения/объединения:

r1 = Rect(1,2,3,4)
r2 = Rect(2,3,4,5)
r3 = Rect(10,20,30,40)

print(r1.is_intersect_rect(r2))  # True   - пересекаются ли прямоугольники
print(r1 * r2)                   # Rect(2.00, 3.00, 3.00, 4.00) - общий прямоугольник
print(r1 + r2)                   # Rect(1.00, 2.00, 4.00, 5.00)  - описанный прямоугольник

print(r1.is_intersect_rect(r3))  # False
print(r1 * r3)                   # Rect(0.00, 0.00, 0.00, 0.00)
print((r1 * r3).is_null())       # True
print(r1 + r3)                   # ect(1.00, 2.00, 30.00, 40.00)

Также имеет несколько дополнительный методов:

r1 = Rect(1,2,3,4)
r2 = Rect(2,3,4,5)

print(r1.area())       # 4.0  Площадь 
print(r1.perimeter())  # 8.0  Периметр

p1 = Vec2(0,0)
p2 = (2, 3)
print(r1.intersect(r2) )   # Rect(2.00, 3.00, 3.00, 4.00) пересечение двух прямоугольников
print(r1.intersect((p1,p2)) ) # (1.33, 2.00) пересечение c отрезком (p1,p2)
print(r1.intersect(p1,p2) )   # (1.33, 2.00) пересечение c отрезком (p1,p2)
print(r1.intersect((p1,p2)))  # (1.33, 2.00) пересечение c отрезком (p1,p2)
print(r1.intersect(s=(p1,p2)))  # (1.33, 2.00) пересечение c отрезком (p1,p2)
print(r1.intersect(r=(p1,p2)) ) # (1.33, 2.00) пересечение c лучом (p1,p2)
print(r1.intersect(line=(p1,p2)) ) # (1.33, 2.00) пересечение c линией (p1,p2)

Полигон/полилиния `PolyLine`

Содержит 3 поля:

vecs - list[Vec2] - список из точек полигона
enclosed - [bool] - флаг, является ли полилиния замкнутой
bbox - Rect - описанный вокруг точек прямоугольник

Примеры импорта и создания:

from easyvec import PolyLine

pg1 = PolyLine([(1,2), (3,4), (2,5)])  
pg2 = PolyLine([(1,2), (3,4), (2,5)], enclosed=True)  
pg3 = PolyLine([Vec2(1,2), Vec2(3,4), Vec2(2,5)], copy_data=False)  
pg4 = PolyLine.from_dict({'vecs': [{'x': 1, 'y': 2}, {'x':3, 'y':4}, {'x': 2, 'y': 5}], 'enclosed': False})

Имеет следующие полезные методы: | имя | что делает | |:------------- |:---------------| | copy() | возвращает копию полигона | | clone() | возвращает копию полигона | | to_dict| возвращает представление полигона в виде словаря | | is_in(self, Vec2 point) | проверяет, находится ли точка внутри полигона | | transform(self, Mat2 m) | возвращает новый полигон точки которого являются произведением исходных точек с матрицей Mat2 m | | add_vec(self, Vec2 v) | возвращает новый полигон точки которого являются смещением исходных точек на вектор v | | get_area(self, bint always_positive=True) | возвращает площадь полигона | | get_center_mass(self) | Получить координату ц.м. полигона (полигон считается с равномерной по полщади плотностью) | | get_Iz(self, Vec2 z_point) | Получить момент инерции относительно оси, проходящей через z_point и направленной перпендикулярно плоскости xy (полигон считается с равномерной по полщади плотностью и массой = 1) | | is_selfintersect(self) | Пересекает ли полигон сам себя | | intersect_line(self, Vec2 p1, Vec2 p2, bint sortreduce=True) | Функция возвращает точки пересечения прямоугольника и линии. sortreduce - нужно ли сортировать точки по расстоянию от p1 | | intersect_ray(self, Vec2 p1, Vec2 p2, bint sortreduce=True) | Функция возвращает точки пересечения прямоугольника и луча. sortreduce - нужно ли сортировать точки по расстоянию от p1 | | intersect_segment(self, Vec2 p1, Vec2 p2, bint sortreduce=True) | Функция возвращает точки пересечения прямоугольника и отрезка. sortreduce - нужно ли сортировать точки по расстоянию от p1 |

Некоторые дополнительные функции

from easyvec.geometry import intersect, closest, normalize_angle2pi, angle_between

# у всех функций есть документация:
print(intersect.__doc__)

    # Возвращает точку пересечения двух сущностей (или None, если они не перечекаются).
    # В качестве сущностей могут быть бесконечные линии, лучи, отрезки, дуги.
    # Сущности задаются двумя точками, через которые они проходят (кроме дуг, они задаются центром, радиусом, и двумя углами).
    # К сожалению, пока нельзя найти пересечение двух дуг(

    # Отрезки задаются кортежем (p1, p2) - двумя крайними точками отрезка. И обозначить их можно именованными аргументами: 
    #     'segment', 's', 'segment1', 's1', 'segment2', 's2',
    # также если аргументы не именованы, то они будут интерпретированы как точки для отрезков. 

    # Лучи задаются кортежем (p1, p2) - точкой, из которой испускается луч, и точкой, через которую он проходит. 
    # И обозначить их можно именованными аргументами: 
    #     'ray', 'r', 'ray1', 'r1', 'ray2', 'r2'

    # Бесконечные линии задаются кортежем (p1, p2) - двумя точками, через которые проходит линия. 
    # И обозначить их можно именованными аргументами:
    #     'line', 'l', 'line1', 'l1', 'line2', 'l2'

    # Дуга задаются кортежем (ctnter, r, angle_from, angle_to) - центром окружности дуги, радиусом, начальным и конечным углом. 
    # И обозначить ее можно именованными аргументами:
    #     'arc', 'a'


    # Примеры использования:
    #     >>> p_intersect = intersect(p1, p2, p3, p4)                 # p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, s=(p3, p4))           # p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, segment=(p3, p4))     # p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, s2=(p3, p4))          # p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)

    #     >>> p_intersect = intersect(s=(p1, p2), s2=(p3, p4))    # p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(s1=(p1, p2), s2=(p3, p4))   # p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(s=(p1, p2), segment=(p3, p4))# p_intersect есть пересечение двух отрезков (p1, p2) и (p3, p4)

    #     >>> p_intersect = intersect(p1, p2, ray=(p3, p4))          # p_intersect есть пересечение отрезка (p1, p2) и луча (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, r=(p3, p4))            # p_intersect есть пересечение отрезка (p1, p2) и луча (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, ray2=(p3, p4))         # p_intersect есть пересечение отрезка (p1, p2) и луча (p3, p4)

    #     >>> p_intersect = intersect(r1=(p1, p2), r2=(p3, p4))    # p_intersect есть перечечение двух лучей (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(r1=(p1, p2), ray2=(p3, p4))  # p_intersect есть перечечение двух лучей (p1, p2) и (p3, p4)
    #     >>> p_intersect = intersect(s=(p1, p2), ray2=(p3, p4))   # p_intersect есть перечечение отрезка (p1, p2) и луча (p3, p4)

    #     >>> p_intersect = intersect(p1, p2, line=(p3, p4))         # p_intersect есть пересечение отрезка (p1, p2) и линии (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, l=(p3, p4))            # p_intersect есть пересечение отрезка (p1, p2) и линии (p3, p4)
    #     >>> p_intersect = intersect(p1, p2, l1=(p3, p4))           # p_intersect есть пересечение отрезка (p1, p2) и линии (p3, p4)

    #     >>> p_intersect = intersect(p1, p2, a=(p3, r, a1, a2))     # p_intersect есть пересечение отрезка (p1, p2) и дуги (p3, r, a1, a2)
    #     >>> p_intersect = intersect(p1, p2, arc=(p3, r, a1, a2))   # p_intersect есть пересечение отрезка (p1, p2) и дуги (p3, r, a1, a2)
    #     и т.д.

    # В качестве p1, p2, p3, p4 могут быть Vec2, кортежи, списки, массивы.... Всё, что поддерживает индексацию [0] и [1], возвращая при этом числа


print(closest.__doc__)

# Возвращает ближайшую точку на сущности к другой, заданной точке
#     В качестве сущности могут быть бесконечные линии, лучи, отрезки.
#     Сущности задаются двумя точками, через которые они проходят

#     Отрезки задаются кортежем (p1, p2) - двумя крайними точками отрезка. И обозначить их можно именованными аргументами: 
#         'segment', 's', 'segment1', 's1', 'segment2', 's2',
#     также если аргументы не именованы, то они будут интерпретированы как точки для отрезков. 

#     Лучи задаются кортежем (p1, p2) - точкой, из которой испускается луч, и точкой, через которую он проходит. 
#     И обозначить их можно именованными аргументами: 
#         'ray', 'r', 'ray1', 'r1', 'ray2', 'r2'

#     Бесконечные линии задаются кортежем (p1, p2) - двумя точками, через которые проходит линия. 
#     И обозначить их можно именованными аргументами:
#         'line', 'l', 'line1', 'l1', 'line2', 'l2'

#     Заданную точку можно обозанчить именованными аргументами:
#         'point', 'p'


#     Примеры использования:
#         >>> p_nearest = closest(p1, p2, p)       # p_nearest есть ближайшая точка к точке "p", и которая принадлежит отрезку (p1, p2)
#         >>> p_nearest = closest(p1, p2, p=p)   # p_nearest есть ближайшая точка к точке "p", и которая принадлежит отрезку (p1, p2)
#         >>> p_nearest = closest(p1, p2, point=p)         # p_nearest есть ближайшая точка к точке "p", и которая принадлежит отрезку (p1, p2)
#         >>> p_nearest = closest(s=(p1, p2), p=p)       # p_nearest есть ближайшая точка к точке "p", и которая принадлежит отрезку (p1, p2)
#         >>> p_nearest = closest(segment=(p1, p2), p=p) # p_nearest есть ближайшая точка к точке "p", и которая принадлежит отрезку (p1, p2)

#         >>> p_nearest = closest(r=(p1, p2), p=p)       # p_nearest есть ближайшая точка к точке "p", и которая принадлежит лучу (p1, p2)
#         >>> p_nearest = closest(ray=(p1, p2), p=p)     # p_nearest есть ближайшая точка к точке "p", и которая принадлежит лучу (p1, p2)

#         >>> p_nearest = closest(line=(p1, p2), p=p)     # p_nearest есть ближайшая точка к точке "p", и которая принадлежит линии (p1, p2)
#         и т.д.

#     В качестве p1, p2, p могут быть Vec2, кортежи, списки, массивы.... Всё, что поддерживает индексацию [0] и [1], возвращая при этом числа



print(normalize_angle2pi.__doc__)

# Нормализвут угол. Приводит его к виду  0 <= angle <= 2*pi


print(angle_between.__doc__)

    # Проверяет лежит ли луч, выходящий из начала координат под углом mid, внутри угла, образаванного двумя лучами,
    # выходящими из начала координат под углами start и end. Область внутри угла образована вращением луча start до луча end против часовой стрелки

продолжение следует...

Project details

Release history Release notifications | RSS feed

This version

0.0.20

May 29, 2020

0.0.18

Apr 24, 2020

0.0.17

Apr 20, 2020

0.0.16

Apr 5, 2020

0.0.15

Mar 9, 2020

0.0.14

Mar 9, 2020

0.0.13

Mar 2, 2020

0.0.12

Feb 28, 2020

0.0.11

Feb 28, 2020

0.0.10

Feb 26, 2020

0.0.9

Feb 24, 2020

0.0.8

Feb 24, 2020

0.0.7

Feb 24, 2020

0.0.6

Feb 23, 2020

0.0.5

Feb 12, 2020

0.0.4

Feb 9, 2020

0.0.3

Feb 9, 2020

0.0.2

Feb 9, 2020

0.0.1

Feb 8, 2020

Download files

Download the file for your platform. If you're not sure which to choose, learn more about installing packages.

Files for easyvec, version 0.0.20
Filename, size	File type	Python version	Upload date	Hashes
Filename, size easyvec-0.0.20-cp37-cp37m-win_amd64.whl (740.1 kB)	File type Wheel	Python version cp37	Upload date May 29, 2020	Hashes View
Filename, size easyvec-0.0.20.tar.gz (869.8 kB)	File type Source	Python version None	Upload date May 29, 2020	Hashes View

Hashes for easyvec-0.0.20-cp37-cp37m-win_amd64.whl

Hashes for easyvec-0.0.20-cp37-cp37m-win_amd64.whl
Algorithm	Hash digest
SHA256	`2559db5ed0208f725f13076b87ed7edb2219b4a24f02458b497a8a96e6bf959d`
MD5	`4b5662edff09f802522681703865d51f`
BLAKE2-256	`747a7eec5721e16b9801b044c56fa550ca7dafbab45733a4843d5ae502b3443c`

Hashes for easyvec-0.0.20.tar.gz

Hashes for easyvec-0.0.20.tar.gz
Algorithm	Hash digest
SHA256	`80906db6436cd808e81524a6408a960e08c29778d8f7af5e81d7df8cf771ef2e`
MD5	`5e71a144943ace04636ebeaa254d8448`
BLAKE2-256	`0571ef74b9e21ca65bea6da3de7124b0a560017fab8aabc14e8a41e396ff164a`

easyvec 0.0.20

Navigation

Project links

Statistics

Meta

Maintainers

Classifiers

Project description

Быстрая библиотека векторной алгебры

Установка

2d библиотека

Вектор/точка `Vec2`

Матрица 2х2 `Mat2`

Прямоугольник со сторонами, параллельными осям координат `Rect`

Полигон/полилиния `PolyLine`

Некоторые дополнительные функции

продолжение следует...

Project details

Project links

Statistics

Meta

Maintainers

Classifiers

Release history Release notifications | RSS feed

Download files

easyvec 0.0.20

Navigation

Project links

Statistics

Meta

Maintainers

Classifiers

Project description

Быстрая библиотека векторной алгебры

Установка

2d библиотека

Вектор/точка Vec2

Матрица 2х2 Mat2

Прямоугольник со сторонами, параллельными осям координат Rect

Полигон/полилиния PolyLine

Некоторые дополнительные функции

продолжение следует...

Project details

Project links

Statistics

Meta

Maintainers

Classifiers

Release history Release notifications | RSS feed

Download files

Вектор/точка `Vec2`

Матрица 2х2 `Mat2`

Прямоугольник со сторонами, параллельными осям координат `Rect`

Полигон/полилиния `PolyLine`