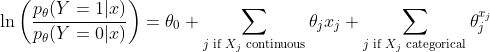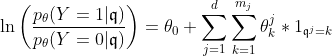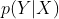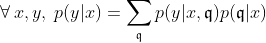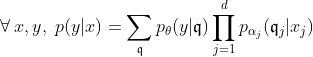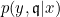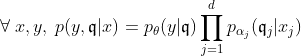glmdisc 0.1.2

Feature quantization for parsimonious and interpretable models

Feature quantization for parsimonious and interpretable models

Table of Contents

• Documentation
• Installation instructions
• Theory
• Some examples
• Open an issue
• References
• Contribute

Motivation

Credit institutions are interested in the refunding probability of a loan given the applicant’s characteristics in order to assess the worthiness of the credit. For regulatory and interpretability reasons, the logistic regression is still widely used to learn this probability from the data. Although logistic regression handles naturally both quantitative and qualitative data, three pre-processing steps are usually performed: firstly, continuous features are discretized by assigning factor levels to pre-determined intervals; secondly, qualitative features, if they take numerous values, are grouped; thirdly, interactions (products between two different predictors) are sparsely introduced. By reinterpreting discretized (resp. grouped) features as latent variables, we are able, through the use of a Stochastic Expectation-Maximization (SEM) algorithm and a Gibbs sampler to find the best discretization (resp. grouping) scheme w.r.t. the logistic regression loss. For detecting interacting features, the same scheme is used by replacing the Gibbs sampler by a Metropolis-Hastings algorithm. The good performances of this approach are illustrated on simulated and real data from Credit Agricole Consumer Finance.

This repository is the implementation of Ehrhardt Adrien, et al. Feature quantization for parsimonious and interpretable predictive models, preprint arXiv:1903.08920 (2019).

Getting started

These instructions will get you a copy of the project up and running on your local machine for development and testing purposes.

Prerequisites

This code is supported on Python 3.7, 3.8, 3.9 and 3.10 (see tox file).

Installing the package

Installing the development version

If git is installed on your machine, you can use:

pip install git+https://github.com/adimajo/glmdisc_python.git

If git is not installed, you can also use:

pip install --upgrade https://github.com/adimajo/glmdisc_python/archive/master.tar.gz

Installing through the pip command

You can install a stable version from PyPi by using:

pip install glmdisc

Installation guide for Anaconda

The installation with the pip command should work. If not, please raise an issue.

For people behind proxy(ies)...

A lot of people, including myself, work behind a proxy at work...

A simple solution to get the package is to use the --proxy option of pip:

pip --proxy=http://username:password@server:port install glmdisc

where username, password, server and port should be replaced by your own values.

If environment variables http_proxy and / or https_proxy and / or (unfortunately depending on applications...) HTTP_PROXY and HTTPS_PROXY are set, the proxy settings should be picked up by pip.

Over the years, I've found CNTLM to be a great tool in this regard.

What follows is a quick introduction to the problem of discretization and how this package answers the question.

Use case example

For a thorough explanation of the approach, see this blog post or this article.

If you're interested in directly using the package, you can skip this part and go to this part below.

In practice, the statistical modeler has historical data about each customer's characteristics. For obvious reasons, only data available at the time of inquiry must be used to build a future application scorecard. Those data often take the form of a well-structured table with one line per client alongside their performance (did they pay back their loan or not?) as can be seen in the following table:

Job	Habitation	Time in job	Children	Family status	Default
Craftsman	Owner	10	0	Divorced	No
Technician	Renter	Missing	1	Widower	No
Missing	Starter	5	2	Single	Yes
Office employee	By family	2	3	Married	No

Notations

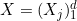
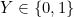
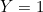
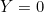
In the rest of the vignette, the random vector will designate the predictive features, i.e. the characteristics of a client. The random variable will designate the label, i.e. if the client has defaulted () or not ().

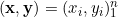
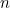
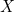
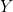
We are provided with an i.i.d. sample consisting in observations of and .

Logistic regression

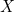
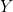
The logistic regression model assumes the following relation between and :

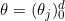
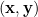
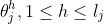
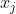
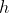
where are estimated using (and denotes the coefficients associated with a categorical feature being equal to ).

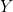
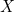
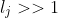
Clearly, for continuous features, the model assumes linearity of the logit transform of the response with respect to . On the contrary, for categorical features, it might overfit if there are lots of levels (). It does not handle missing values.

Common problems with logistic regression on "raw" data

Fitting a logistic regression model on "raw" data presents several problems, among which some are tackled here.

Feature selection

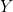
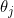
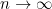
First, among all collected information on individuals, some are irrelevant for predicting . Their coefficient should be 0 which might (eventually) be the case asymptotically (i.e. ).

Second, some collected information are highly correlated and affect each other's coefficient estimation.

As a consequence, data scientists often perform feature selection before training a machine learning algorithm such as logistic regression.

There already exists methods and packages to perform feature selection, see for example the feature_selection submodule in the sklearn package.

glmdisc is not a feature selection tool but acts as such as a side-effect: when a continuous feature is discretized into only one interval, or when a categorical feature is regrouped into only one value, then this feature gets out of the model.

For a thorough reference on feature selection, see e.g. Guyon, I., & Elisseeff, A. (2003). An introduction to variable and feature selection. Journal of machine learning research, 3(Mar), 1157-1182.

Linearity

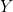
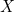
When provided with continuous features, the logistic regression model assumes linearity of the logit transform of the response with respect to . This might not be the case at all.

For example, we can simulate a logistic model with an arbitrary power of 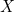and then try to fit a linear logistic model:

• Show the Python code

• Get this graph online

Of course, providing the sklearn.linear_model.LogisticRegression function with a dataset containing 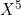would solve the problem. This can't be done in practice for two reasons: first, it is too time-consuming to examine all features and candidate polynomials; second, we lose the interpretability of the logistic decision function which was of primary interest.

Consequently, we wish to discretize the input variable 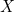into a categorical feature which will "minimize" the error with respect to the "true" underlying relation:

• Show the Python code

• Get this graph online

Too many values per categorical feature

When provided with categorical features, the logistic regression model fits a coefficient for all its values (except one which is taken as a reference). A common problem arises when there are too many values as each value will be taken by a small number of observations 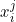which makes the estimation of a logistic regression coefficient unstable:

• Show the Python code

• Get this graph online

If we divide the training set in 10 and estimate the variance of each coefficient, we get:

• Show the Python code

• Get this graph online

All intervals crossing 0 are non-significant! We should group factor values to get a stable estimation and (hopefully) significant coefficient values.

Discretization and grouping: theoretical background

Notations

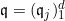
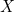
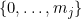
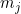
Let be the latent discretized transform of , i.e. taking values in where the number of values of each covariate is also latent.

The fitted logistic regression model is now:

Clearly, the number of parameters has grown which allows for flexible approximation of the true underlying model .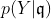

Best discretization?

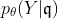
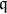
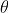
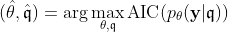
Our goal is to obtain the model with best predictive power. As and are both optimized, a formal goodness-of-fit criterion could be: where AIC stands for Akaike Information Criterion.

Combinatorics

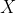
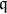
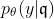
The problem seems well-posed: if we were able to generate all discretization schemes transforming to , learn for each of them and compare their AIC values, the problem would be solved.

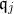
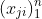
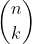
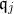
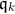
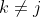
Unfortunately, there are way too many candidates to follow this procedure. Suppose we want to construct k intervals of given n distinct . There is models. The true value of k is unknown, so it must be looped over. Finally, as logistic regression is a multivariate model, the discretization of can influence the discretization of , .

As a consequence, existing approaches to discretization (in particular discretization of continuous attributes) rely on strong assumptions to simplify the search of good candidates as can be seen in the review of Ramírez‐Gallego, S. et al. (2016) - see References section.

Discretization and grouping: estimation

Likelihood estimation

can be introduced in :

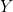
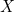
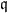
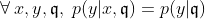
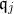
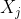
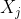
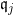
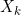
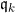
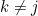
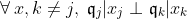
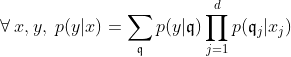
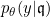
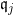
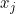
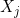
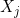
First, we assume that all information about in is already contained in so that: Second, we assume the conditional independence of given , i.e. knowing , the discretization is independent of the other features and for all : The first equation becomes: As said earlier, we consider only logistic regression models on discretized data . Additionnally, it seems like we have to make further assumptions on the nature of the relationship of to . We chose to use polytomous logistic regressions for continuous and contengency tables for qualitative . This is an arbitrary choice and future versions will include the possibility of plugging your own model.

The first equation becomes:

The SEM algorithm

It is still hard to optimize over 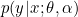as the number of candidate discretizations is gigantic as said earlier.

However, calculating is easy:

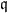
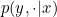
As a consequence, we will draw random candidates approximately at the mode of the distribution using an SEM algorithm (see see References section).

Gibbs sampling

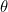
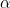
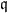
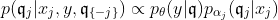
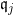
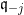
To update, at each random draw, the parameters and and propose a new discretization , we use the following equation: Note that we draw knowing all other variables, especially so that we introduced a Gibbs sampler (see References section).

The glmdisc package

The glmdisc class

The documentation is available as a Github Page.

The glmdisc class implements the algorithm described in the previous section. Its parameters are described first, then its internals are briefly discussed. We finally focus on its ouptuts.

Parameters

The number of iterations in the SEM algorithm is controlled through the iter parameter. It can be useful to first run the glmdisc function with a low (10-50) iter parameter so you can have a better idea of how much time your code will run.

The validation and test boolean parameters control if the provided dataset should be divided into training, validation and/or test sets. The validation set aims at evaluating the quality of the model fit at each iteration while the test set provides the quality measure of the final chosen model.

The criterion parameters lets the user choose between standard model selection statistics like aic and bic and the gini index performance measure (proportional to the more traditional AUC measure). Note that if validation=TRUE, there is no need to penalize the log-likelihood and aic and bic become equivalent. On the contrary if criterion="gini" and validation=FALSE then the algorithm may overfit the training data.

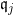
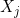
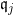
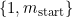
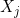
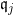
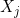
The m_start parameter controls the maximum number of categories of for continuous. The SEM algorithm will start with random taking values in . For qualitative features , is initialized with as many values as so that m_start has no effect.

Empirical studies show that with a reasonably small training dataset (< 10,000 rows) and a small m_start parameter (< 20), approximately 500 to 1500 iterations are largely sufficient to obtain a satisfactory model .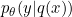

>>> import glmdisc
>>> logreg_disc = glmdisc.Glmdisc(iter=100, validation=True, test=True, criterion="bic", m_start=10)

2020-07-16 18:11:03.087 | WARNING  | glmdisc:__init__:216 - No need to penalize the log-likelihood when a validation set is used. Using log-likelihood instead.

The fit function

The fit function of the glmdisc class is used to run the algorithm over the data provided to it. Subsequently, its parameters are: predictors_cont and predictors_qual which represent respectively the continuous features to be discretized and the categorical features which values are to be regrouped. They must be of type numpy array, filled with numeric and strings respectively. The last parameter is the class labels, of type numpy array as well, in binary form (0/1).

>>> n = 100
>>> d = 2
>>> x, y, _ = glmdisc.Glmdisc.generate_data(n, d)
>>> logreg_disc.fit(predictors_cont=x, predictors_qual=None, labels=y)

The best_formula function

The best_formula function prints out in the console: the cut-points found for continuous features, the regroupments made for categorical features' values. It also returns it in a list.

>>> logreg_disc.best_formula()

2020-07-16 18:13:29.921 | INFO     | glmdisc._bestFormula:best_formula:29 - Cut-points found for continuous variable 0
[0.9568289154869697, 0.6661178585993954, 0.49039089060451335, 0.33038638461067193, 0.7152644679549544]
2020-07-16 18:13:29.922 | INFO     | glmdisc._bestFormula:best_formula:29 - Cut-points found for continuous variable 1
[0.48684331022166916, 0.17904111281801316, 0.6603144758481163, 0.03838803248009037]

The discrete_data function

The discrete_data function returns the discretized / regrouped version of the predictors_cont and predictors_qual arguments using the best discretization scheme found so far.

>>> logreg_disc.discrete_data()

2020-07-16 18:14:57.261 | INFO     | glmdisc._discreteData:discrete_data:44 - Returning discretized test set.
<20x11 sparse matrix of type '<class 'numpy.float64'>'
	with 40 stored elements in Compressed Sparse Row format>

>>> logreg_disc.discrete_data().toarray()

2020-07-16 18:15:31.041 | INFO     | glmdisc._discreteData:discrete_data:44 - Returning discretized test set.
array([[1., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 0., 1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 0.],
[...]

The discretize function

The discretize function discretizes a new input dataset in the predictors_cont, predictors_qual format using the best discretization scheme found so far. The result is a numpy array of the size of the original data.

>>> n_new = 100
>>> x_new, _, _ = glmdisc.Glmdisc.generate_data(n_new, d)
>>> logreg_disc.discretize(predictors_cont=x_new, predictors_qual=None)

array([[4., 1.],
       [5., 2.],
       [4., 3.],
       [4., 4.],
       [3., 4.],
       [0., 2.],
[...]

The discretize_dummy function

The discretize_dummy function discretizes a new input dataset in the predictors_cont, predictors_qual format using the best discretization scheme found so far. The result is a dummy (0/1) numpy array corresponding to the One-Hot Encoding of the result provided by the discretize function.

>>> logreg_disc.discretize_dummy(predictors_cont=x_new, predictors_qual=None)

<100x11 sparse matrix of type '<class 'numpy.float64'>'
	with 200 stored elements in Compressed Sparse Row format>

>>> logreg_disc.discretize_dummy(predictors_cont=x_new, predictors_qual=None).toarray()

array([[0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 1., 0., 0.],
       [0., 0., 0., ..., 0., 1., 0.],
       ...,
       [1., 0., 0., ..., 1., 0., 0.],
       [1., 0., 0., ..., 0., 0., 0.],
       [1., 0., 0., ..., 0., 0., 0.]])

The predict function

The predict function discretizes a new input dataset in the predictors_cont, predictors_qual format using the best discretization scheme found so far through the discretizeDummy function and then applies the corresponding best Logistic Regression model 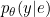found so far.

>>> logreg_disc.predict(predictors_cont=x_new, predictors_qual=None)

array([[9.99394254e-01, 6.05745839e-04],
       [9.99694576e-01, 3.05424466e-04],
       [9.99817560e-01, 1.82439609e-04],
       [9.99967791e-01, 3.22085041e-05],
       [9.92296119e-01, 7.70388116e-03],
[...]

The attributes

All parameters are stored as attributes: test, validation, criterion, iter, m_start as well as:

• criterion_iter: list of values of the criterion chosen;

>>> logreg_disc.criterion_iter

[-30.174443117243992, -26.182075441528603, -31.61227858514535, -19.70369464830396, -31.61997286396158, -25.99964499964587, ...]

• best_link: link function of the best quantization;

>>> logreg_disc.best_link

[LogisticRegression(C=1e+40, max_iter=25, multi_class='multinomial',
                   solver='newton-cg', tol=0.001), 
LogisticRegression(C=1e+40, max_iter=25, multi_class='multinomial',
                   solver='newton-cg', tol=0.001)]

• best_reglog: logistic regression function of the best quantization;

>>> logreg_disc.best_reglog

LogisticRegression(C=1e+40, max_iter=25, solver='liblinear', tol=0.001)

• affectations: list of label encoders for categorical features;

>>> logreg_disc.affectations

[None, None]

• best_encoder_emap: one hot encoder of the best quantization;

>>> logreg_disc.best_encoder_emap

OneHotEncoder(handle_unknown='ignore')

• performance: value of the chosen criterion for the best quantization;

>>> logreg_disc.performance

-14.924603930263428

• train: array of row indices for training samples;

>>> logreg_disc.train

array([97, 39, 94,  5, 16, 77, 88, 54, 80, 99, 46, 43, 52, 37, 28,  0, 18, ...

• validate: array of row indices for validation samples;

>>> logreg_disc.validate

array([36, 45, 29, 62,  8, 82, 76, 96, 41, 83, 17, 49, 57, 31, 60, 64, 65, ...

• test_rows: array of row indices for test samples;

>>> logreg_disc.test_rows

array([ 3, 75, 51, 27, 21, 48,  4, 44, 72, 68, 34, 22, 23, 50, 47,  6, 42, ...

To see the package in action, please refer to the accompanying Jupyter Notebook.

• Do a notebook

Authors

• Adrien Ehrhardt
• Vincent Vandewalle
• Philippe Heinrich
• Christophe Biernacki

License

This project is licensed under the MIT License - see the LICENSE file for details.

Acknowledgments

This research has been financed by Crédit Agricole Consumer Finance through a CIFRE PhD.

This research was supported by Inria Lille - Nord-Europe and Lille University as part of a PhD.

References

Ehrhardt, A. (2019), Formalization and study of statistical problems in Credit Scoring: Reject inference, discretization and pairwise interactions, logistic regression trees (PhD thesis).

Ehrhardt, A., et al. Feature quantization for parsimonious and interpretable predictive models. arXiv preprint arXiv:1903.08920 (2019)].

Celeux, G., Chauveau, D., Diebolt, J. (1995), On Stochastic Versions of the EM Algorithm. [Research Report] RR-2514, INRIA. 1995.

Agresti, A. (2002) Categorical Data. Second edition. Wiley.

Ramírez‐Gallego, S., García, S., Mouriño‐Talín, H., Martínez‐Rego, D., Bolón‐Canedo, V., Alonso‐Betanzos, A. and Herrera, F. (2016). Data discretization: taxonomy and big data challenge. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 6(1), 5-21.

Future development: integration of interaction discovery

Very often, predictive features $X$ "interact" with each other with respect to the response feature. This is classical in the context of Credit Scoring or biostatistics (only the simultaneous presence of several features - genes, SNP, etc. is predictive of a disease).

With the growing number of potential predictors and the time required to manually analyze if an interaction should be added or not, there is a strong need for automatic procedures that screen potential interaction variables. This will be the subject of future work.

Future development: possibility of changing model assumptions

In the third section, we described two fundamental modelling hypotheses that were made:

• The real probability density function $p(Y|X)$ can be approximated by a logistic regression $p_\theta(Y|E)$ on the discretized data $E$.
• The nature of the relationship of $\mathfrak{q}_j$ to $X_j$ is:
• A polytomous logistic regression if $X_j$ is continuous;
• A contengency table if $X_j$ is qualitative.

These hypotheses are "building blocks" that could be changed at the modeller's will: discretization could optimize other models.

• To delete when done with

Results

First we simulate a "true" underlying discrete model:

x = matrix(runif(300), nrow = 100, ncol = 3)
cuts = seq(0,1,length.out= 4)
xd = apply(x,2, function(col) as.numeric(cut(col,cuts)))
theta = t(matrix(c(0,0,0,2,2,2,-2,-2,-2),ncol=3,nrow=3))
log_odd = rowSums(t(sapply(seq_along(xd[,1]), function(row_id) sapply(seq_along(xd[row_id,]),
function(element) theta[xd[row_id,element],element]))))
y = rbinom(100,1,1/(1+exp(-log_odd)))

The glmdisc function will try to "recover" the hidden true discretization xd when provided only with x and y:

library(glmdisc)
discretization <- glmdisc(x,y,iter=50,m_start=5,test=FALSE,validation=FALSE,criterion="aic",interact=FALSE)

library(glmdisc)
discretization <- glmdisc(x,y,iter=50,m_start=5,test=FALSE,validation=FALSE,criterion="aic",interact=FALSE)

How well did we do?

To compare the estimated and the true discretization schemes, we can represent them with respect to the input "raw" data x:

plot(x[,1],xd[,1])
plot([e-mail][,1],[e-mail][,1])

Contribute

You can clone this project using:

git clone https://github.com/adimajo/glmdisc_python.git

You can install all dependencies, including development dependencies, using (note that this command requires pipenv which can be installed by typing pip install pipenv):

pipenv install -d

You can build the documentation by going into the docs directory and typing make html.

NOTE: you need to have a separate folder named glmdisc_python_docs in the same directory as this repository, as it will build the docs there so as to allow me to push this other directory as a separate gh-pages branch.

You can run the tests by typing coverage run -m pytest, which relies on packages coverage and pytest.

To run the tests in different environments (one for each version of Python), install pyenv (see the instructions here), install all versions you want to test (see tox.ini), e.g. with pyenv install 3.7.0 and run pipenv run pyenv local 3.7.0 [...] (and all other versions) followed by pipenv run tox.