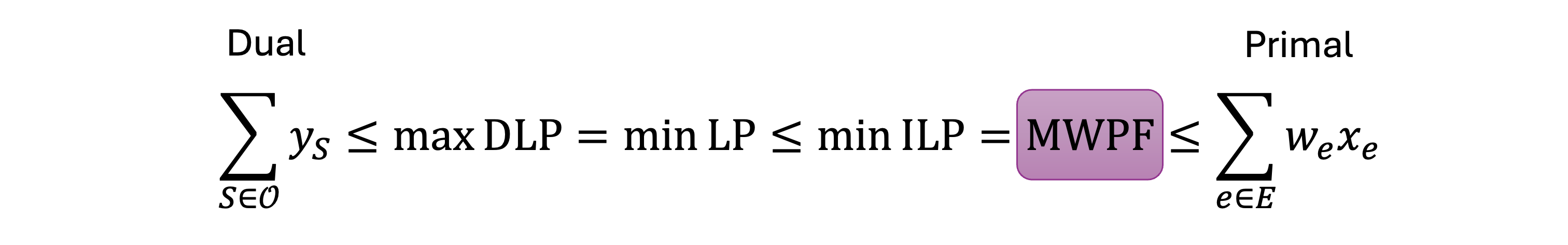Hypergraph Minimum-Weight Parity Factor (MWPF) Solver for Quantum LDPC Codes
Project description
MWPF
Hypergraph Minimum-Weight Parity Factor Decoder for QEC
Preview claim: We publish the Python package that may subject to breaking changes. The source code and the full version will be made publicly available with our coming paper.
Hypergraph MWPF is proven to be NP-hard [1]. Our design is taking advantage of clustering technique to lower the average time complexity and reach almost-linear average time complexity at small physical error rate. Please wait for our paper for more discussion of the speed v.s. accuracy.
Installation
pip install MWPF
Background
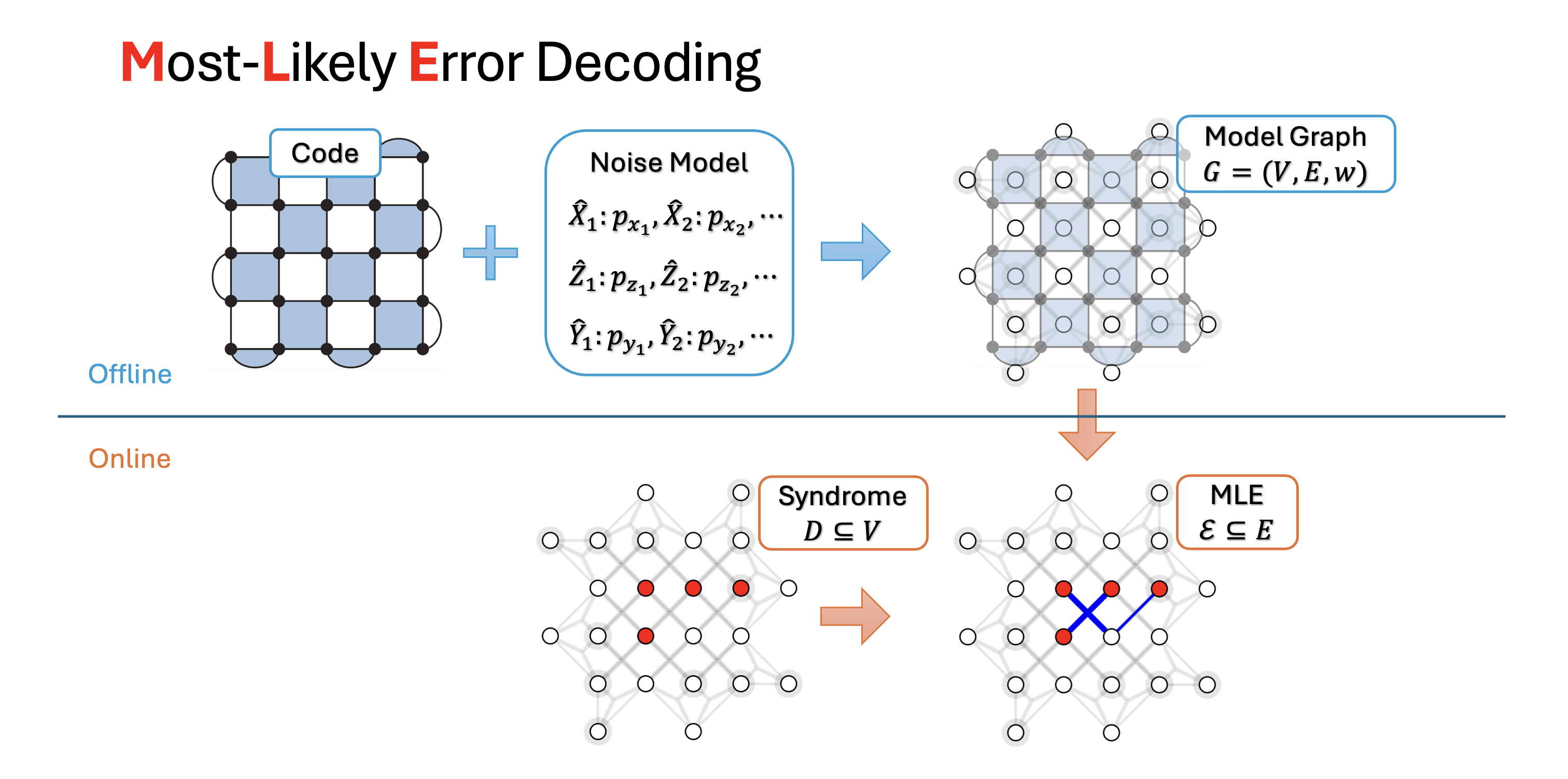
The Most-Likely Error (MLE) decoding problem can be formulated as a MWPF problem.
Naming
We named it Minimum-Weight Parity Factor because of a concept called "parity $(g,f)$-factor" in Lovász's 1972 paper [2]. In the context of QEC, the functions $g(v)$ and $f(v)$ associates with the measured syndrome as shown above. Without ambiguity, we just call it "parity factor".
Relationship with MWPM decoder
Minimum-Weight Perfect Matching decoder is the traditional decoder for QEC. When the decoding graph is a simple graph, the MLE decoding problem can be reduced to an MWPM problem on a generated complete graph with $O(|V|^2)$ edges. Two recent works [2] and [3] improves the average time complexity to almost theoretical upper bound of $O(|V|)$ by not explicitly generating the complete graph. This motivates our idea to design an algorithm directly on the model graph, hoping to reach the same $O(|V|)$ average time complexity even if the model graph is hypergraph.
Key Idea
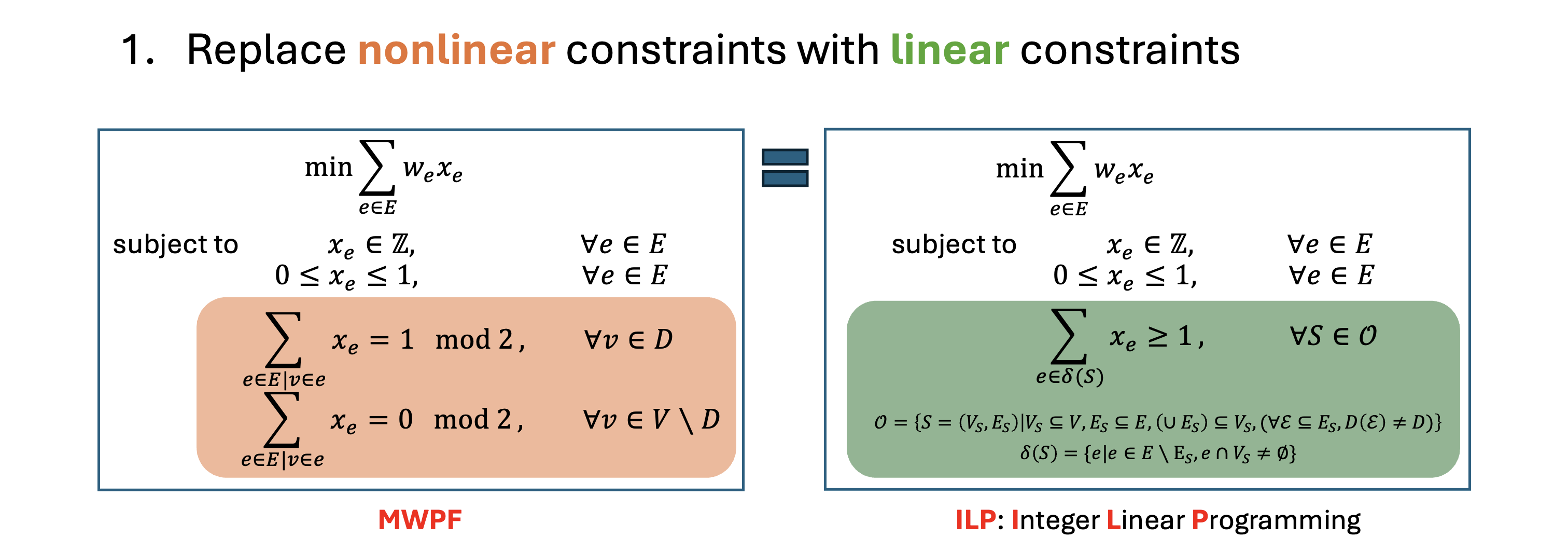
We try to extend the blossom algorithm that solves the MWPM problem on simple graphs. An interesting attribute of the blossom algorithm is that it deals with an exponential number of linear constraints in order to relax the integer constraints. The added linear constraints, which we refer to as "blossom constraints", are based on a very simple idea: filtering out invalid solutions. The blossom constraints simply say "any odd cluster cannot be perfectly matched internally", which is obviously true. However, this "filtering" requires an exponential number of linear constraints [5], which is impossible to generate efficiently. Thus, the algorithm must implicitly consider those exponential number of constraints without ever listing them. In fact, the blossom algorithm only keeps track of $O(|V|)$ such constraints from the exponentially many. Surprisingly, this works! Inspired by this miracle, we now have the courage to use an exponential number of linear constraints to solve MWPF.
Rigorous Math
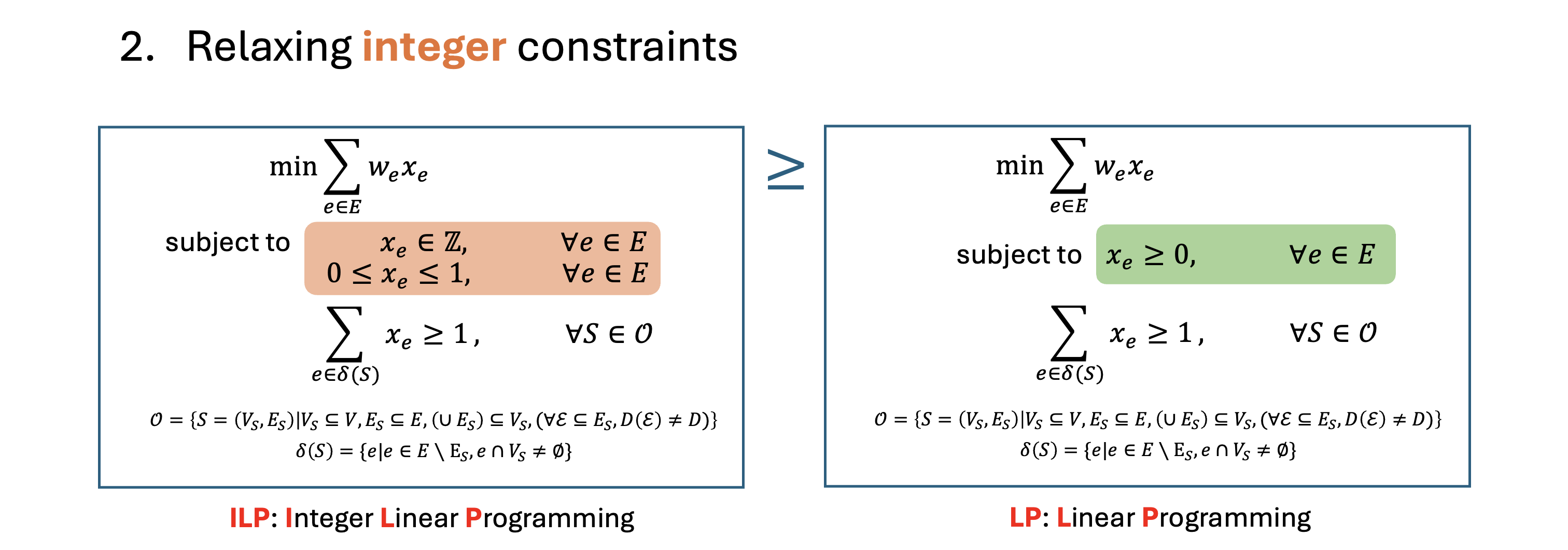
The ILP problem above is very similar to that of the blossom algorithm, except for the more complex "blossom"definition: it's now a subgraph $S=(V_S, E_S), V_S \subseteq V, E_S \subseteq E$ instead of just a subset of vertices $S\subseteq V$ in the blossom algorithm. We have mathematically proved the equivalence between hypergraph MWPF and this ILP. In the next step, we simply relax the integer constraints.
Clearly, as a relaxation, the minimum objective value is no larger than that of the ILP. Unfortunately, we haven't been able to rigorously prove that they have the same optimal objective value, nor can we find a counter example. We leave this conjecture as is for now, and do not assume its correctness.
Conjecture: $\min\text{ILP}=\min\text{LP}$.
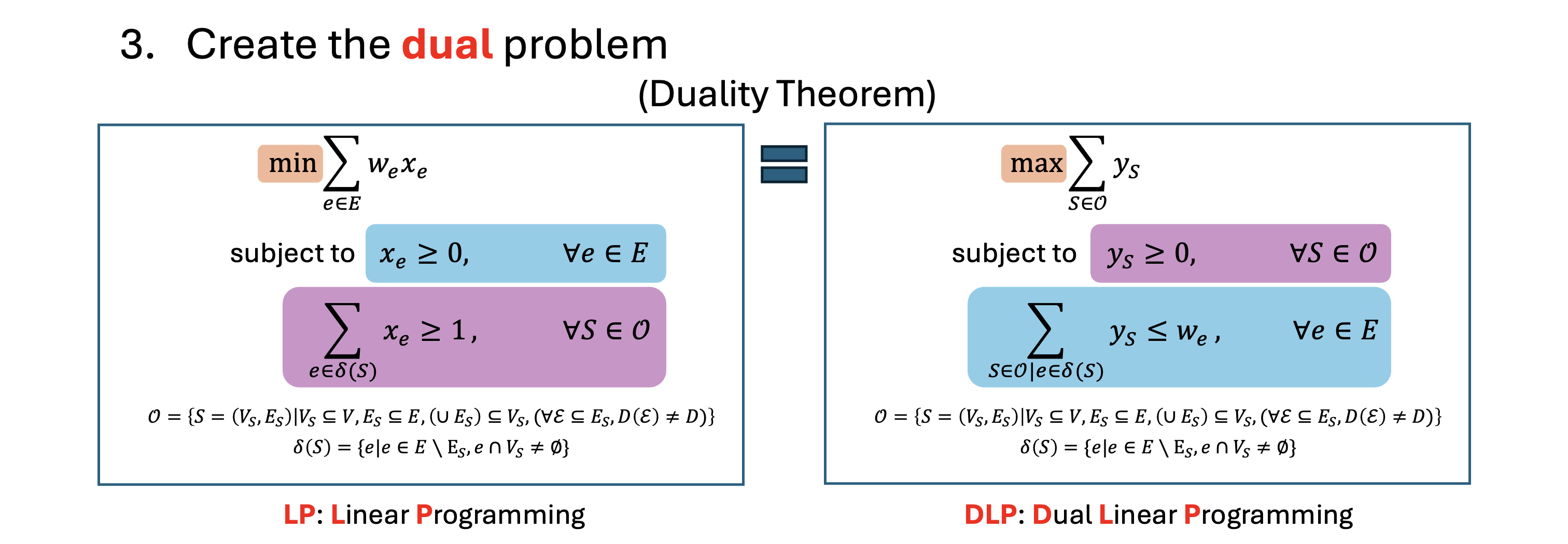
The dual problem is a transpose of the primal LP problem. According to the duality theorem, they have the same optimal value. The key is that each primal constraint becomes a dual variable, and each primal variable becomes a dual constraint. Clearly, for the dual problem, $y_S = 0, \forall S \in \mathcal{O}$ is a solution (despite usually not the optimal solution). In this way, we can keep track of only non-zero dual variables to implicitly considering all the exponentially many primal constraints. Since the dual LP problem becomes a maximization problem, we have the whole inequality chain as below.
If we can find a pair of feasible primal and dual solutions with the same weight, then this inequality chain collapses to an equality chain and the primal solution is proven to be optimal. Even if they are not equal, we still get a proximity bound.
In fact, MWPM decoder using the blossom algorithm fits in this framework, where the alternating tree operation guarantees that in the end the primal must be equal to the dual. Union-Find decoder and hypergraph UF decoder can also be explained by this framework, but the proximity bound is usually not singleton.
Usage
The decoding process is two steps (shown in Background)
- offline: construct the model graph given the QEC code and the noise model
- online: compute the most-likely error $\mathcal{E}\subseteq E$ given the syndrome (represented by the defect vertices $D \subseteq V$) and some dynamic weights
from mwpf import HyperEdge, SolverInitializer, SolverSerialJointSingleHair, SyndromePattern
# Offline
vertex_num = 4
weighted_edges = [
HyperEdge([0, 1], 100), # [vertices], weight
HyperEdge([1, 2], 100),
HyperEdge([2, 3], 100),
HyperEdge([0], 100), # boundary vertex
HyperEdge([0, 1, 2], 60), # hyperedge
]
initializer = SolverInitializer(vertex_num, weighted_edges)
hyperion = SolverSerialJointSingleHair(initializer)
# Online
syndrome = [0, 1, 3]
hyperion.solve(SyndromePattern(syndrome))
hyperion_subgraph = hyperion.subgraph()
print(hyperion_subgraph) # out: [3, 5], weighted 160
_, bound = hyperion.subgraph_range()
print((bound.lower, bound.upper)) # out: (Fraction(160, 1), Fraction(160, 1))
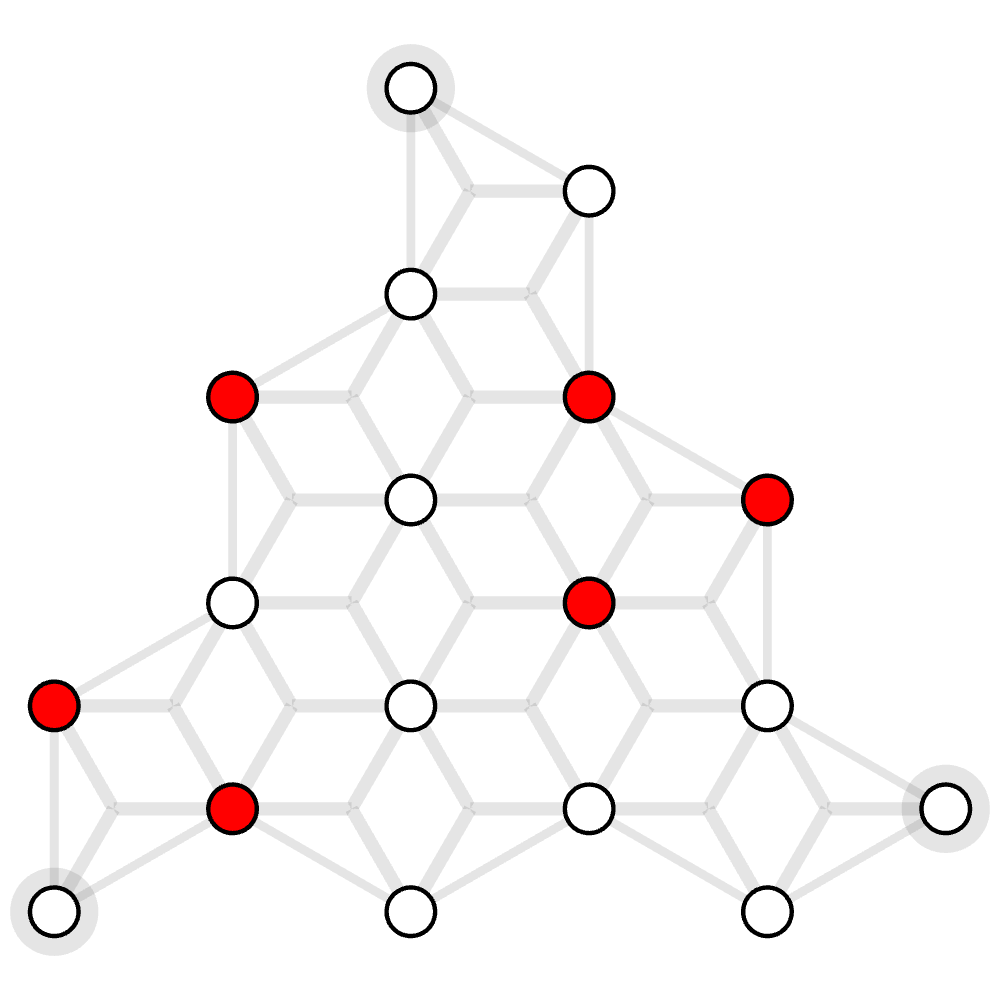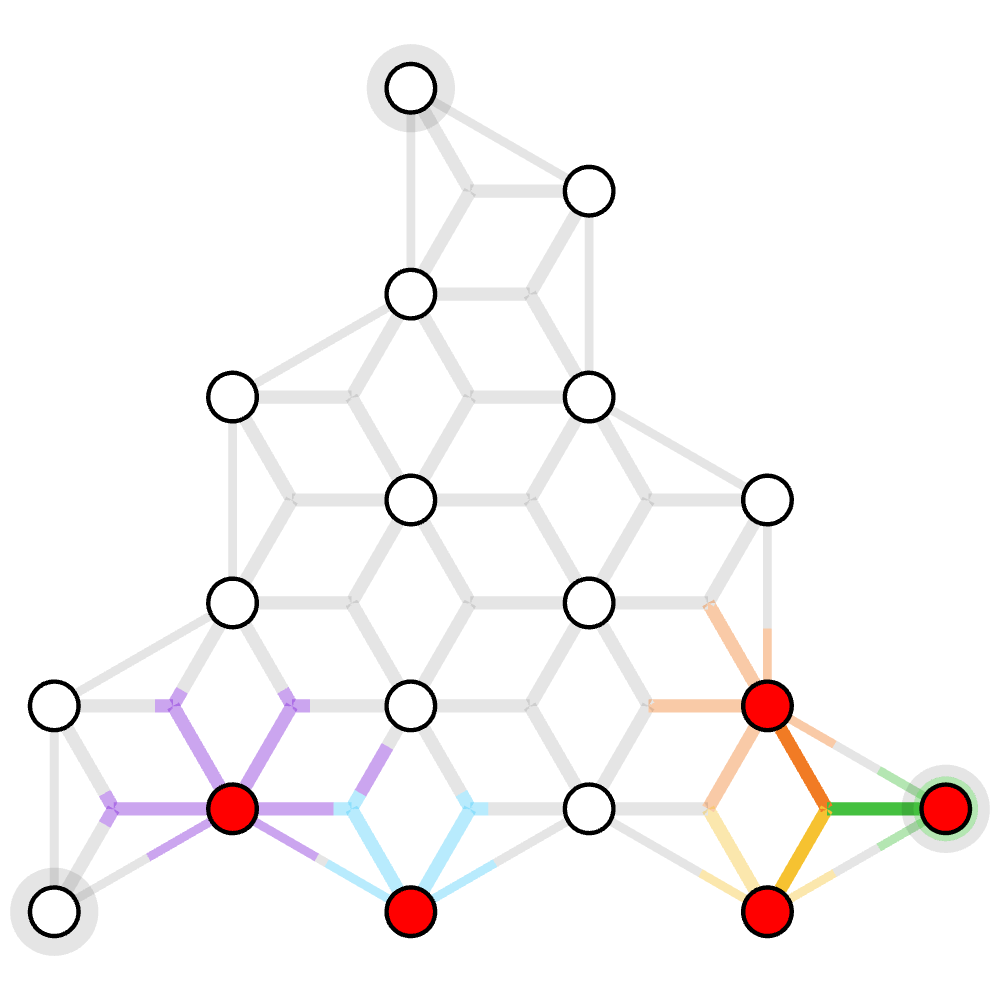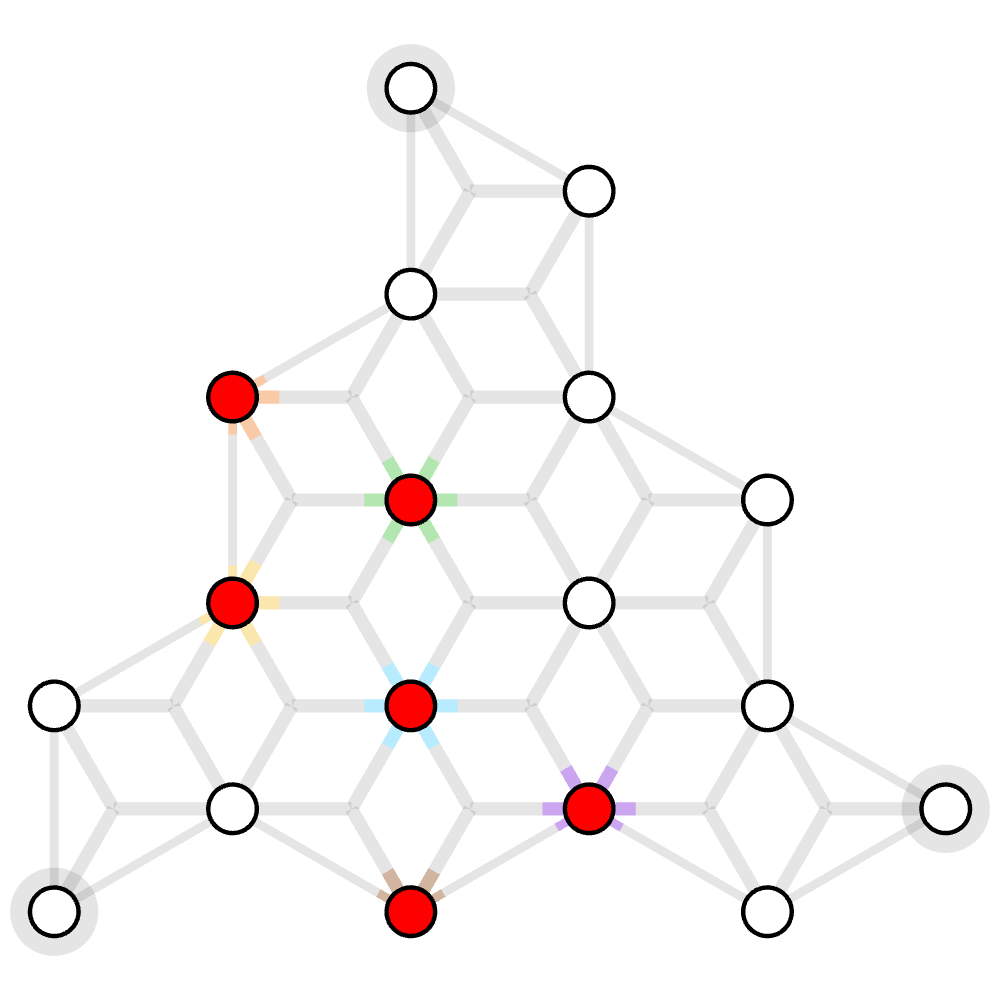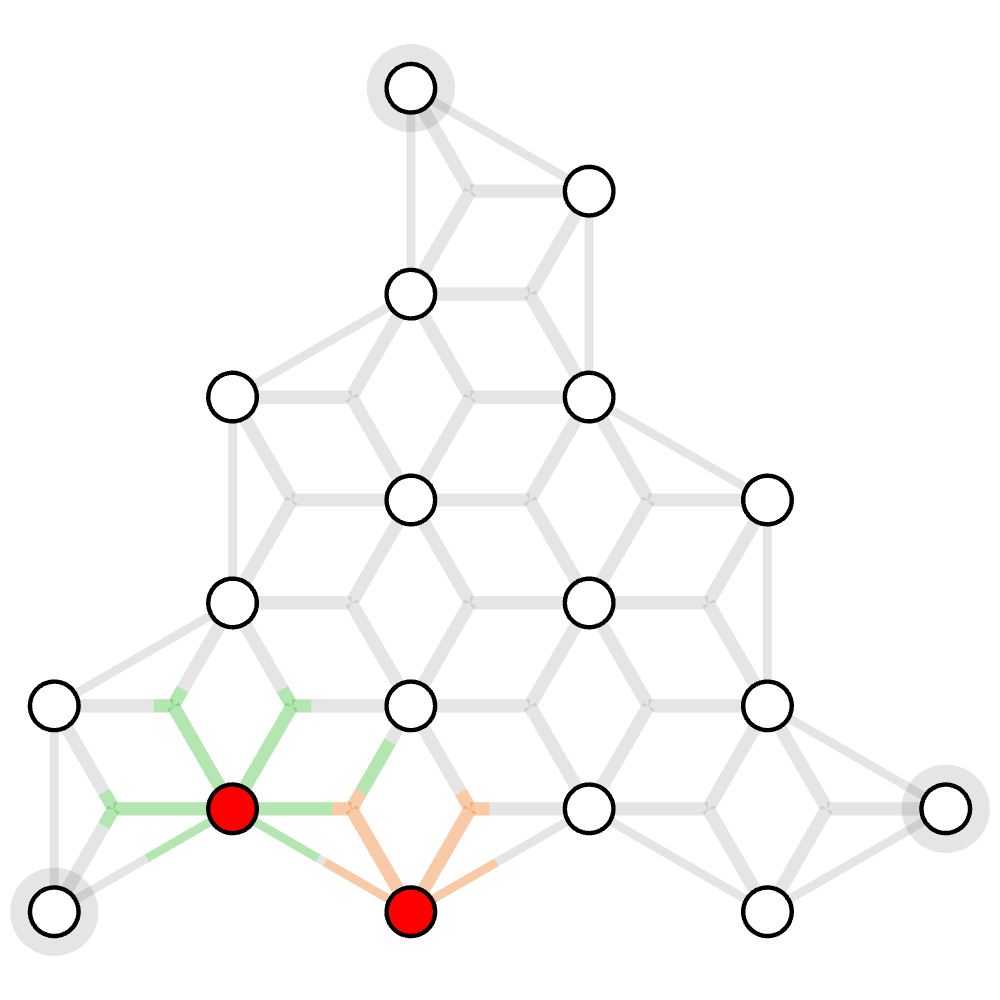
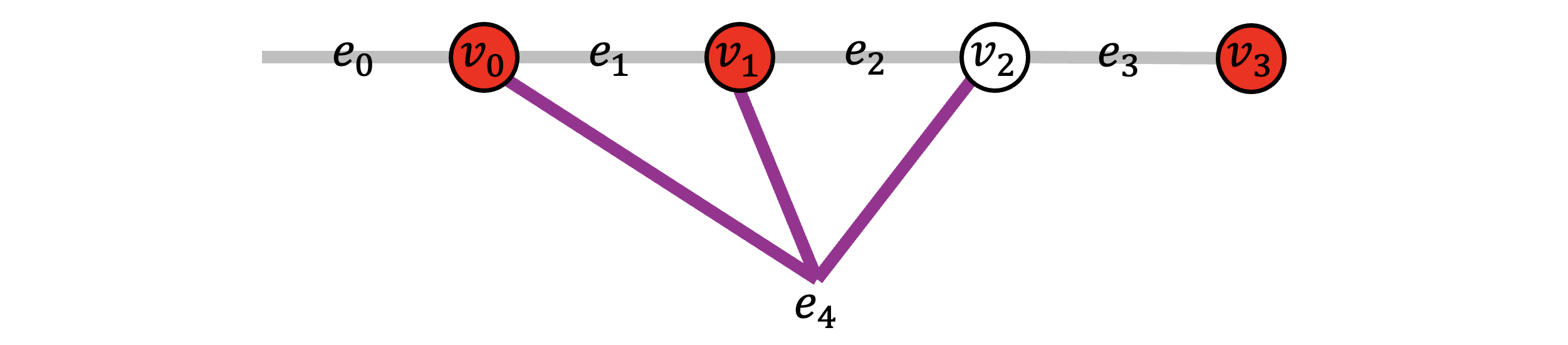
The example hyergraph is below: grey edges are weighted 100 and the purple hyperedge is weighted 60.
In constrast, if we were to solve MWPF with MWPM decoder, then we have to ignore the hyperedge $e_4$ and thus leads to suboptimal result, as shown by the following Python script using the Fusion Blossom library.
from fusion_blossom import SolverInitializer, SolverSerial, SyndromePattern
# Offline
vertex_num = 5
weighted_edges = [(0, 4, 100), (0, 1, 100), (1, 2, 100), (2, 3, 100)]
virtual_vertices = [4]
initializer = SolverInitializer(vertex_num, weighted_edges, virtual_vertices)
fusion = SolverSerial(initializer)
# Online
syndrome = [0, 1, 3]
fusion.solve(SyndromePattern(syndrome))
fusion_subgraph = fusion.subgraph()
print(fusion_subgraph) # out: [0, 2, 3], which is weighted 300 instead of 160
Advanced Usage
When trading off accuracy and decoding time, we provide a timeout parameter for the decoder. Also, one can specify whether you want the clusters to all grow together or grow one by one. More parameters are coming as we develop the library.
config = {
"primal": {
"timeout": 3.0, # 3 second timeout for each cluster
},
"growing_strategy": "SingleCluster", # growing from each defect one by one
# "growing_strategy": "MultipleClusters", # every defect starts to grow at the same time
}
hyperion = SolverSerialJointSingleHair(initializer, config)
An embedded visualization tool is coming soon.
Examples
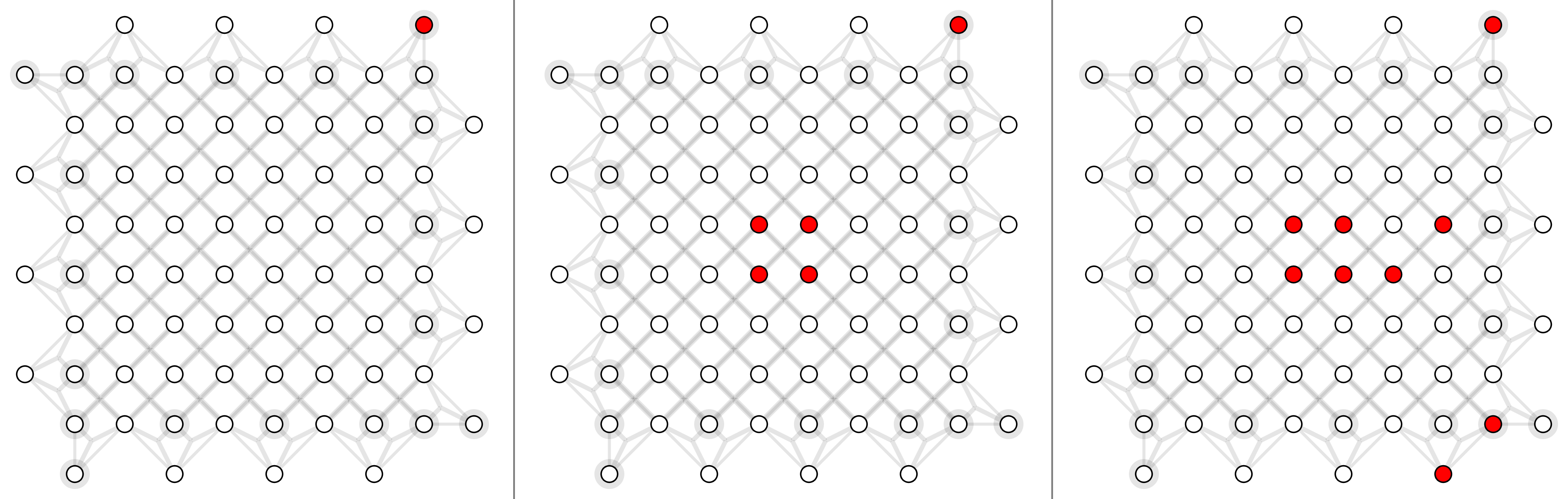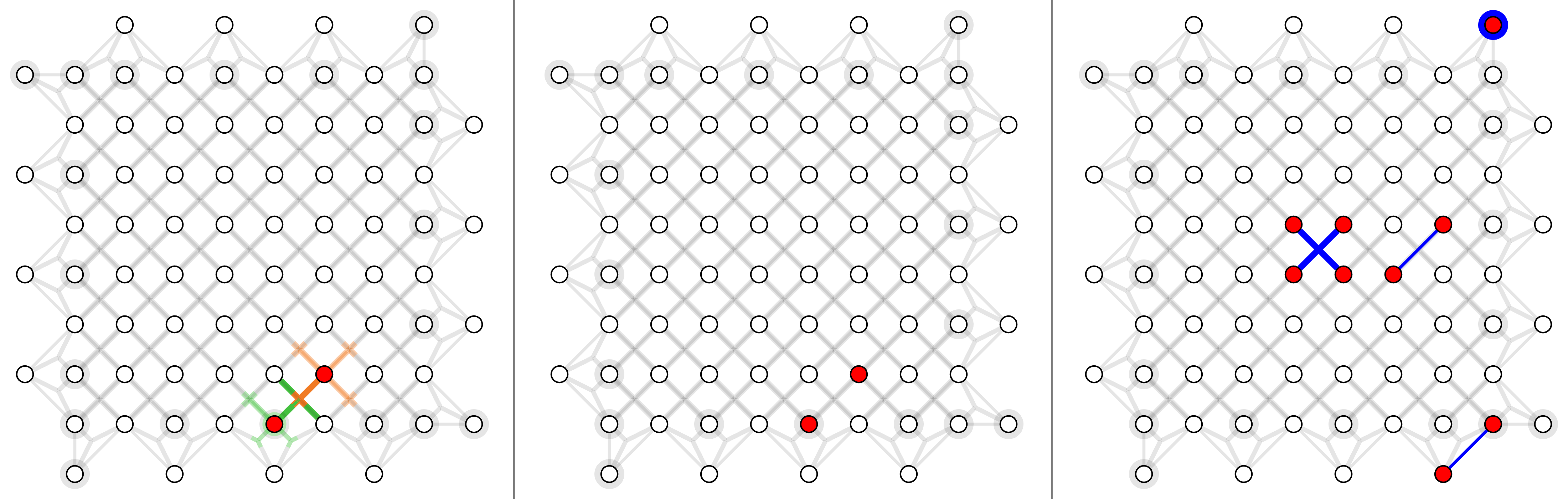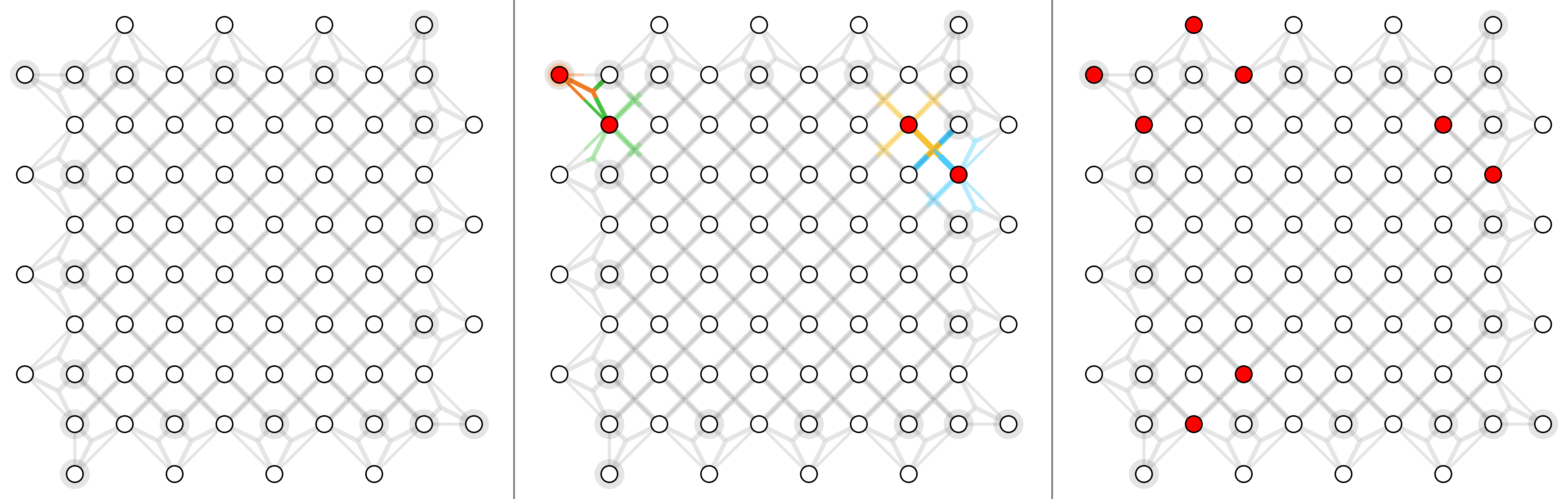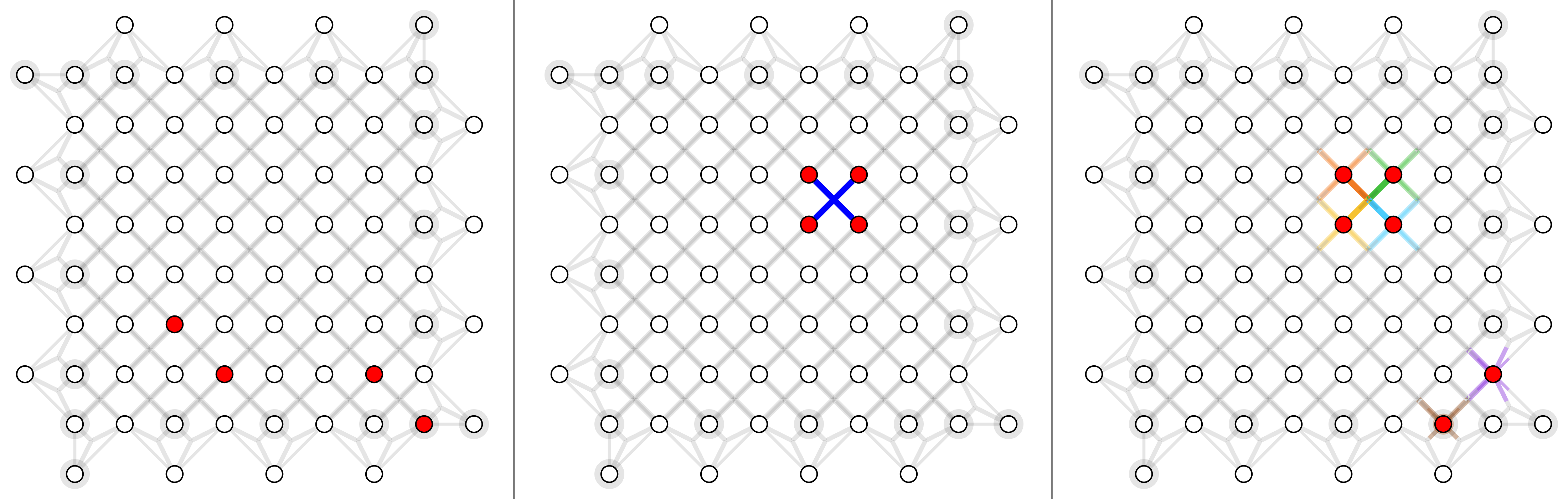
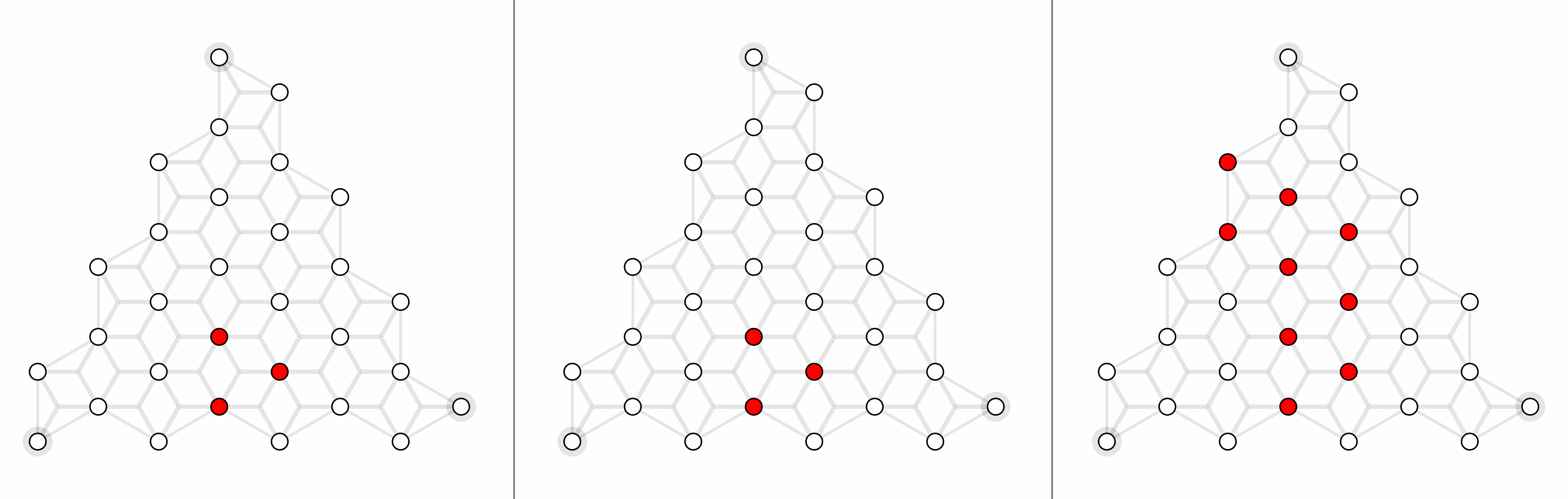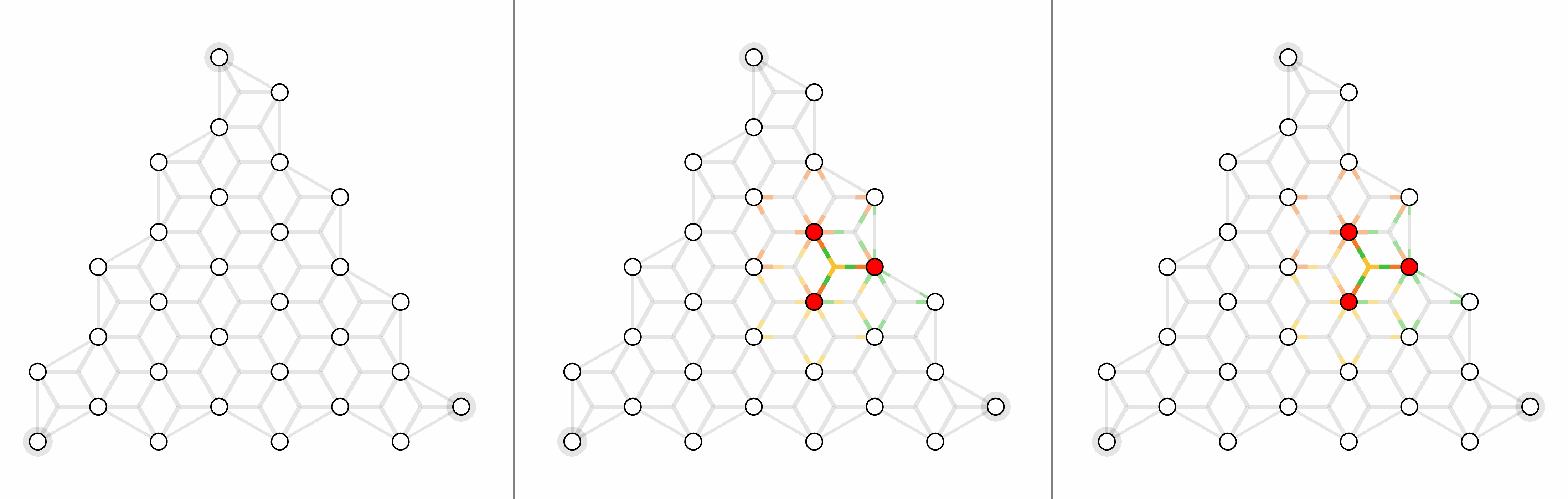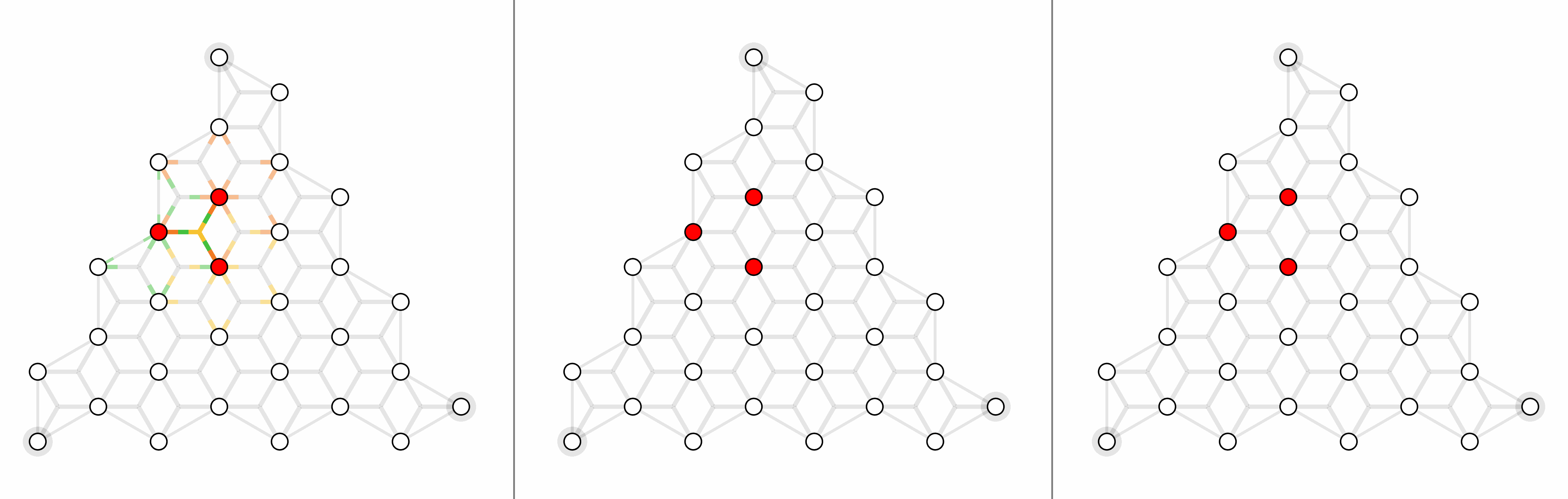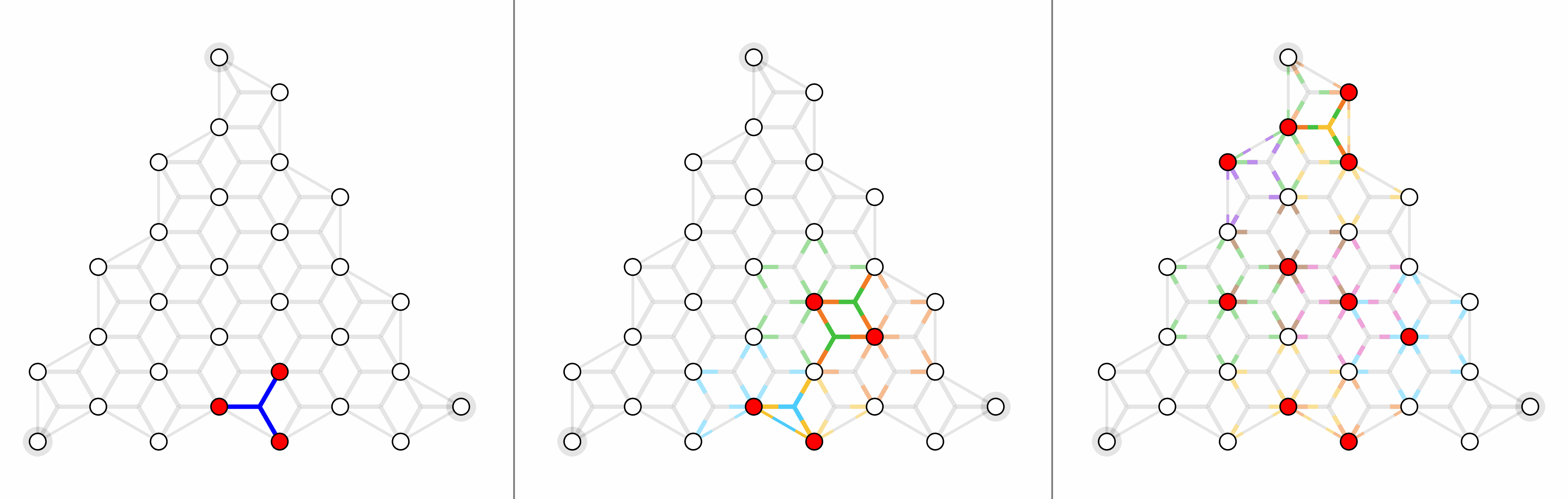
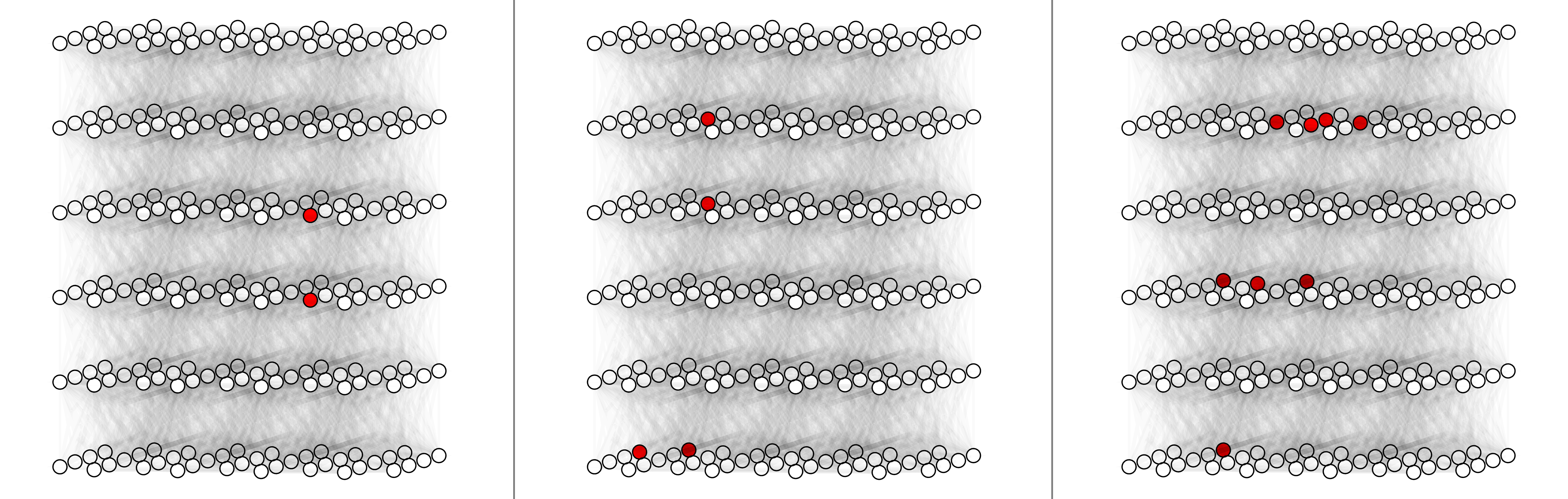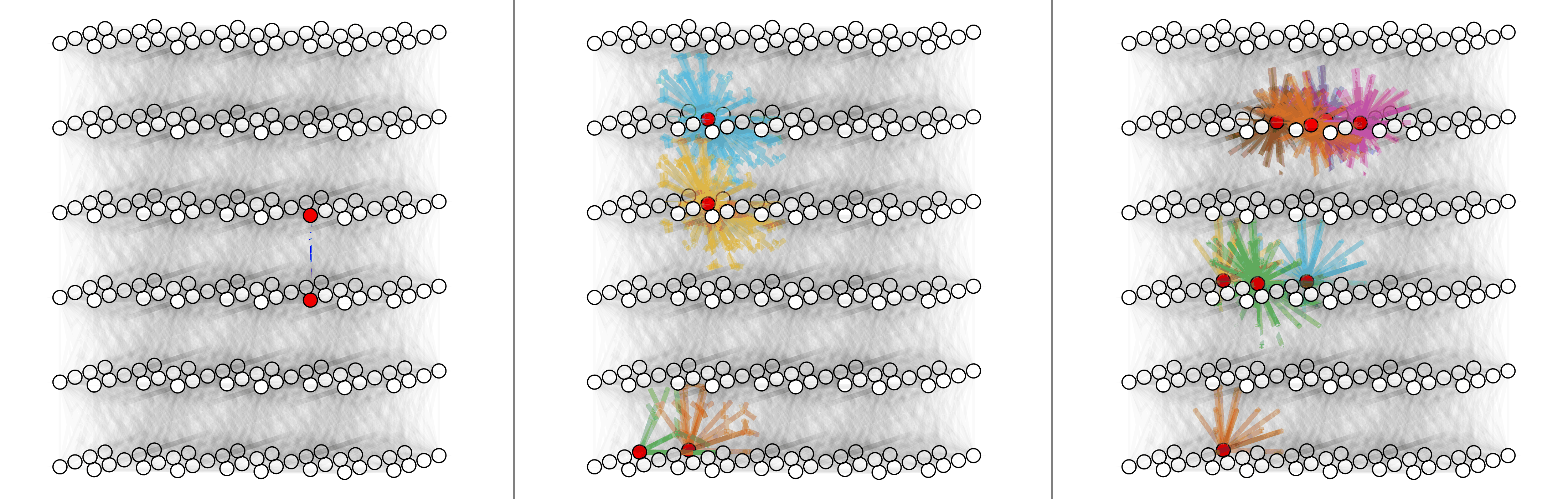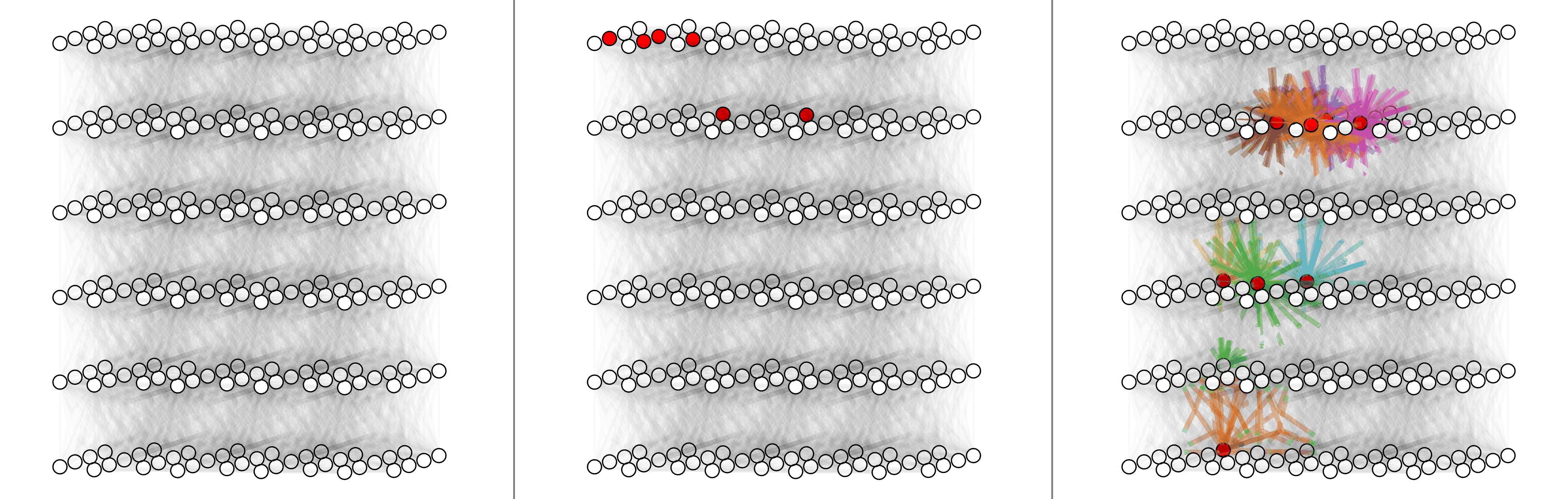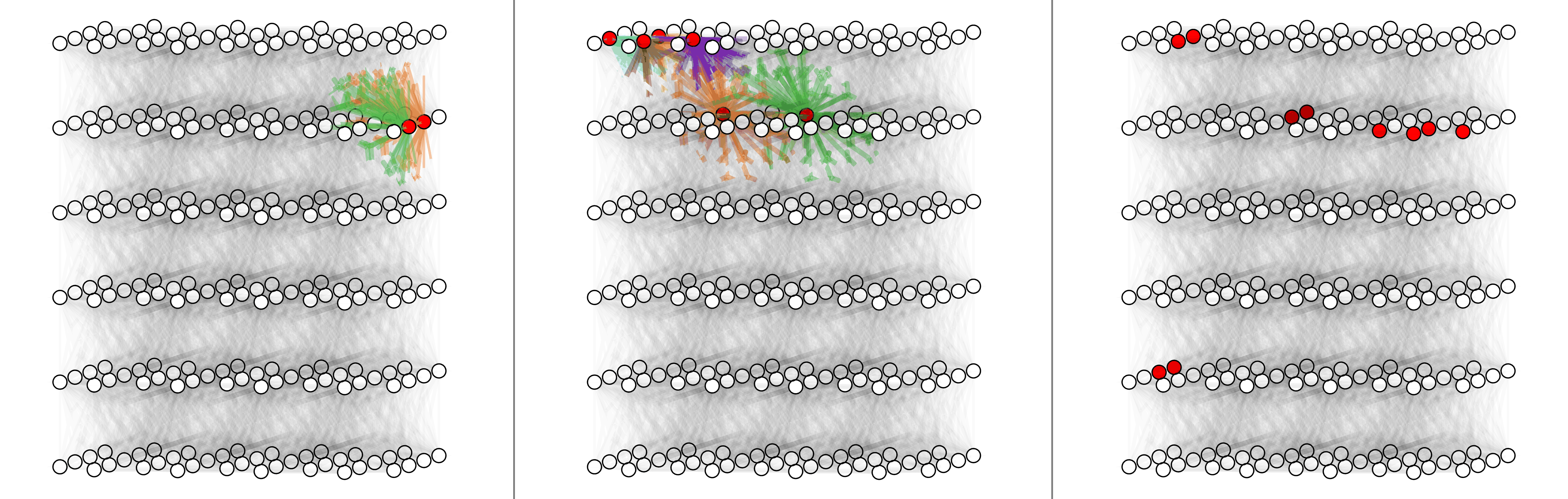
For surface code with depolarizing noise mode $p_x =p_y=p_z = p/3$, here shows physical error rates 1%, 2% and 4% (left to right).
For triangle color code with X errors, here shows physical error rates 1%, 2% and 4% (left to right).
For circuit-level surface code, here shows physical error rate 0.03%, 0.1% and 0.3% (left to right).
Reference
[1] Berlekamp, Elwyn, Robert McEliece, and Henk Van Tilborg. "On the inherent intractability of certain coding problems (corresp.)." IEEE Transactions on Information Theory 24.3 (1978): 384-386.
[2] Lovász, László. "The factorization of graphs. II." Acta Mathematica Academiae Scientiarum Hungarica 23 (1972): 223-246.
[3] Higgott, Oscar, and Craig Gidney. "Sparse Blossom: correcting a million errors per core second with minimum-weight matching." arXiv preprint arXiv:2303.15933 (2023).
[4] Wu, Yue, and Lin Zhong. "Fusion Blossom: Fast MWPM Decoders for QEC." arXiv preprint arXiv:2305.08307 (2023).
[5] Rothvoß, Thomas. "The matching polytope has exponential extension complexity." Journal of the ACM (JACM) 64.6 (2017): 1-19.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distributions
Built Distributions
File details
Details for the file mwpf-0.1.5-cp37-abi3-win_amd64.whl.
File metadata
- Download URL: mwpf-0.1.5-cp37-abi3-win_amd64.whl
- Upload date:
- Size: 2.9 MB
- Tags: CPython 3.7+, Windows x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.0.0 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 18063965e8967d607a19402cc33454f810dfb78acec19a71321f527ad1de39ff |
|
| MD5 | d5801bcaccdef070416347faa9a40da5 |
|
| BLAKE2b-256 | 1e2390ff9829cf4395854ba0ef15560f7e9a534c912c56bc0357fcd5ed4eb471 |
File details
Details for the file mwpf-0.1.5-cp37-abi3-musllinux_1_2_x86_64.whl.
File metadata
- Download URL: mwpf-0.1.5-cp37-abi3-musllinux_1_2_x86_64.whl
- Upload date:
- Size: 19.4 MB
- Tags: CPython 3.7+, musllinux: musl 1.2+ x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.0.0 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 0bd62e5ba53ad3ae3d74be6c56fbbf1f9376cc77a04fa820ecc49c059f12ff48 |
|
| MD5 | c856739f1516e3749221771f7420dd14 |
|
| BLAKE2b-256 | 00327912dc6d48411728959d67cea6e8a78baffe15c95f119176d289dac1a3e3 |
File details
Details for the file mwpf-0.1.5-cp37-abi3-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: mwpf-0.1.5-cp37-abi3-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 18.4 MB
- Tags: CPython 3.7+, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.0.0 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 79393b79640db30f38e0b90fccc21c6357fc0364c0884b7d04dfab1692dde483 |
|
| MD5 | b4abf3524a2ac552b28c14f928289536 |
|
| BLAKE2b-256 | f12cd1af1d0604163f863c39dfc9d614bbf0a4c6ec72aa14019b1ad6f4f5a9ba |
File details
Details for the file mwpf-0.1.5-cp37-abi3-macosx_10_12_universal2.whl.
File metadata
- Download URL: mwpf-0.1.5-cp37-abi3-macosx_10_12_universal2.whl
- Upload date:
- Size: 6.2 MB
- Tags: CPython 3.7+, macOS 10.12+ universal2 (ARM64, x86-64)
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.0.0 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 57c5dd63a3c6fa14d84bdc8f929ec91f2c92abaac2df23f7eb0fe7ca33d18363 |
|
| MD5 | c0e2f0949124feeeed93f1fa5284b02d |
|
| BLAKE2b-256 | 4bc43a816a8145000b3858f7275a32294ecd5f86294b991ddf2c6acd88d82570 |