Implement the Empirical Bayes ranking scheme developed in Kline, Rose, and Walters (2023)
Project description
DRrank
DRrank is a Python library to implement the Empirical Bayes ranking scheme developed in Kline, Rose, and Walters (2023). This code was originally developed by Hadar Avivi.
Installation:
The package uses the Gurobi optimizer. To use DRrank you must first install Gurobi and acquire a license. More guidance is available from Gurobi here. Gurobi offers a variety of free licenses for academic use. For more information, see the following page.
After having successfully set up Gurobipy, install DRrank via pip:
pip install drrank
Usage
1. Load sample data
DRrank grades units based on noisy estimates of a latent attribute. You can construct these estimates however you'd like---all DRrank requires is a vector of estimates, $\hat{\theta}_i$, and their associated standard errors, $s_i$.
To illustrate the package's features, this readme uses the data in example/name_example.csv, which contains estimates of name-specific contact rates from the experiment studied in Kline, Rose, and Walters (2023). These contact rates have been adjusted to stabilize their variances using the Bartlett (1936) transformation. Variance-stabilization is useful because the deconvolution procedure used in Step 2 below requires that $s_i$ be independent of $\theta_i$. In cases where variance stabilization is not possible, independence can sometimes be restored by residualizing $\hat{\theta_i}$ against $s_i$; see Section 5 of Kline, Rose, and Walters (2023) for a detailed example. The transformation used in our names example computes estimates as $\hat{\theta}_i = sin^{-1} \sqrt{\hat{p}_i}$, where $\hat{p}_i$ is share of applications with name $i$ that received a callback. As discussed in the paper, $\hat{\theta}_i$ has asymptotic variance of $(4N_i)^{-1}$, where $N_i$ is the number of applications sent with name $i$.
import pandas as pd
import os
# Read in the data
data = pd.read_csv(os.getcwd() + '/example/name_example.csv')
data.head()
| name_id | thetas | s | firstname |
|---|---|---|---|
| 1 | 0.53788 | 0.0137214 | Adam |
| 2 | 0.518394 | 0.0173332 | Aisha |
| 3 | 0.53767 | 0.0174933 | Allison |
| 4 | 0.532129 | 0.0138126 | Amanda |
| 5 | 0.534998 | 0.0136503 | Amy |
While DRrank provides the functionality to account for any variance-stabilizing transformation, using one is not strictly necessary. DRrank can also accomodate cases where the $\hat{\theta}_i$ directly capture untransformed estimates of the relevant latent attribute.
2. Estimating the prior
DRrank provides the functionality to estimate a prior distribution using a variation on Efron (2016)'s log-spline deconvolution approach, which uses an exponential family mixing distribution with density parameterized by a flexible B-th order natural cubic spline.
To estimate the prior, generate an instance of the prior_estimate class with each unit's estimated latent attribute, $\hat{\theta}_i$, and its associated standard errors. You also have the option of supplying an inverse transform in case the $\hat{\theta}_i$ have been transformed to stabilize variances. The appropriate inverse transform for the ranking name-specific contact rates in Kline, Rose, and Walters (2023), for example, is $f(x) = sin(x)^2$. The inverse transform function should be vectorized.
import numpy as np
from drrank_distribution import prior_estimate
thetas = data.thetas.values # set of estimates
s = data.s.values # setstandard errors
# Initialize the estimator
G = prior_estimate(thetas, s, transform=lambda x: np.power(np.sin(x),2))
# Estimate the prior distribution
G.estimate_prior(supp_points=5000, spline_order=5, seed = 123)
Use the supp_points option (default=5000) to pick the number of points of support over which to evaluate the prior density. The minimum and maximum of the support are the minimum and maximum of thetas.
Use the spline_order option (default=5) to adjust the degrees of freedom of the spline that parameterizes the mixing distribution.
The estimated prior distribution will be saved as a dictionary. You can access it with the following code:
# Dictionary with the prior distribution
G.prior_g
# Keys:
# mean_theta: mean of the prior
G.prior_g['mean_theta']
# sd_theta: standard deviation of the prior
G.prior_g['sd_theta']
# g_theta: estimated prior density
G.prior_g['g_theta']
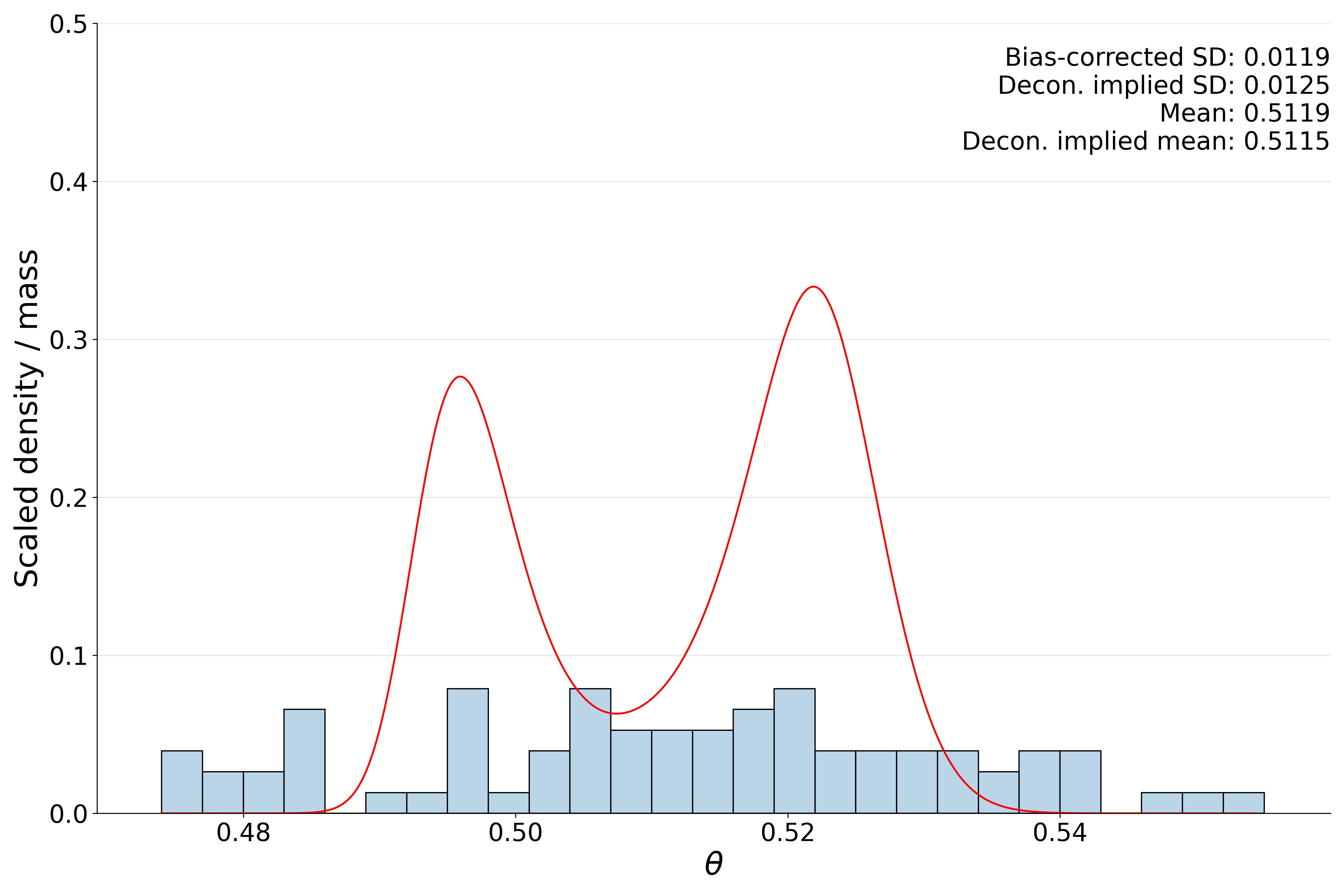
You can then graph the results by calling the following function:
# Plot the estimated prior distribution
G.plot_estimates(save_path = "example/prior_distribution.jpg",
binwidth = 0.0030,
line_kws = {'alpha': 0.6},
fill = True,
alpha = 0.3)
Within the function you can specify the following arguments:
- g_theta: provide your own prior distribution G.
Noneimplies the function will utilize the estimated G from the estimate_prior() method (default =None). - show_plot: whether to show the plot or not (default =
True). - save_path: path to where the plot will be saved.
Noneimplies the graph will not be saved (default =None).
You can also furtherly change the visualization of the histogram, which inherits all the arguments from seaborn.histplot
3. Estimation of posterior features and $P$ matrix
Once the prior distribution has been estimated, you can estimate posterior means and credible intervals, as well as the matrix of pairwise posterior ordering probabilities $P$.
# Compute the posterior features
G.compute_posteriors(alpha=.05, g_theta=None)
G.pmean # posterior means
G.pmean_trans # inverse transformed posterior means
G.lci # lower limit of 1-alpha credible interval
G.uci # upper limit of 1-alpha credible interval
G.lci_trans # lower limit of inverse transformed 1-alpha credible interval
G.uci_trans # upper limit of inverse transformed 1-alpha credible interval
G.posterior_df.head() # Dataframe of posterior features
| pmean | pmean_trans | lci | uci | lci_trans | uci_trans | |
|---|---|---|---|---|---|---|
| 0 | 0.522524 | 0.249088 | 0.50771 | 0.532169 | 0.236368 | 0.257458 |
| 1 | 0.515032 | 0.242678 | 0.493166 | 0.529646 | 0.224124 | 0.255255 |
| 2 | 0.52051 | 0.247361 | 0.497425 | 0.531542 | 0.227686 | 0.25691 |
| 3 | 0.521265 | 0.248005 | 0.500928 | 0.531446 | 0.23063 | 0.256826 |
| 4 | 0.521993 | 0.248631 | 0.50456 | 0.531815 | 0.233697 | 0.257149 |
Then compute the pairwise ordering probabilities $P$ using:
# Compute the pairwise ordering probabilities
pis = G.compute_pis(g_theta=None, ncores=-1, power=0)
In both functions, it is possible to provide your own prior distribution G by feeding an array as the g_theta argument. This density must take support on the values determined by G.supp_theta.
compute_pis also provides the option to compute the elements of $P$, $\pi_{ij}$, as the posterior expectation of $max(\theta_i - \theta_j,0)^{power}$, providing an extension to weighted ranking exercises. The default, $power=0$, will produce $\pi_{ij}$ that are posterior ordering probabilities discussed in the next section and implies that ranking mistakes a considered equally costly regardless of the cardinal difference between $\theta_i$ and $\theta_j$.
4. Computing grades
To compute rankings, use the fit function with a matrix $P$. In the unweighted case, $P$ reflects the posterior probabilities that observation i's latent measure $\theta_i$ exceeds unit j's. That is, each element of this matrix takes the form:
$\pi_{ij} = Pr(\theta_i > \theta_j | Y_i = y_i, Y_j = y_j)$
DRrank expects these probabilities to satisfy $\pi_{ij} = 1-\pi_{ji}$ and will report a warning if that does not appear to be the case.
In the weighted case, $P$ captures expected differences between i and j's value of $\theta$, as discussed above.
There are two ways to use DRrank.
First, one can supply a parameter $\lambda \in [0,1]$, which corresponds to the user's value of correctly ranking pairs of units relative to the costs of misclassifying them. $\lambda=1$ implies correct and incorrect rankings are valued equally, while $\lambda=0$ implies correct rankings are not valued at all. In the unweighted case, it is optimal to assign unit $i$ a higher grade than unit $j$ when $\pi_{ij} > 1/(1+\lambda)$, which implies $\lambda$ also determines the minimum level of posterior certainty required to rank units pairwise.
from drrank import fit
# Fit the report card function
results = fit(pis, lamb = 0.25, DR = None)
The results object contains the row index of $P$, the assigned grades, and the Condorcet rank (i.e., grade under $\lambda=1$).
| obs_idx | grades_lamb0.25 | condorcet_rank |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 1 | 32 |
| 3 | 1 | 12 |
| 4 | 1 | 9 |
| 5 | 1 | 5 |
We also provide functionality to compute results for a list of values of $\lambda$ in parallel:
import numpy as np
from drrank import fit_multiple
# Try different values of Lambda
results_l = fit_multiple(pis, np.arange(0, 0.9, 0.01))
Second, one can ask DRrank to compute grades that maximize Kendall (1938)'s $\tau$, a measure of the rank correlation between units' latent rankings and assigned grades, subject to a constraint on the expected share of pairwise units incorrectly classified, which we refer to as the Discordance Rate (DR).
# Fit the report card function
results_dr = fit(pis, lamb = None, DR = 0.05)
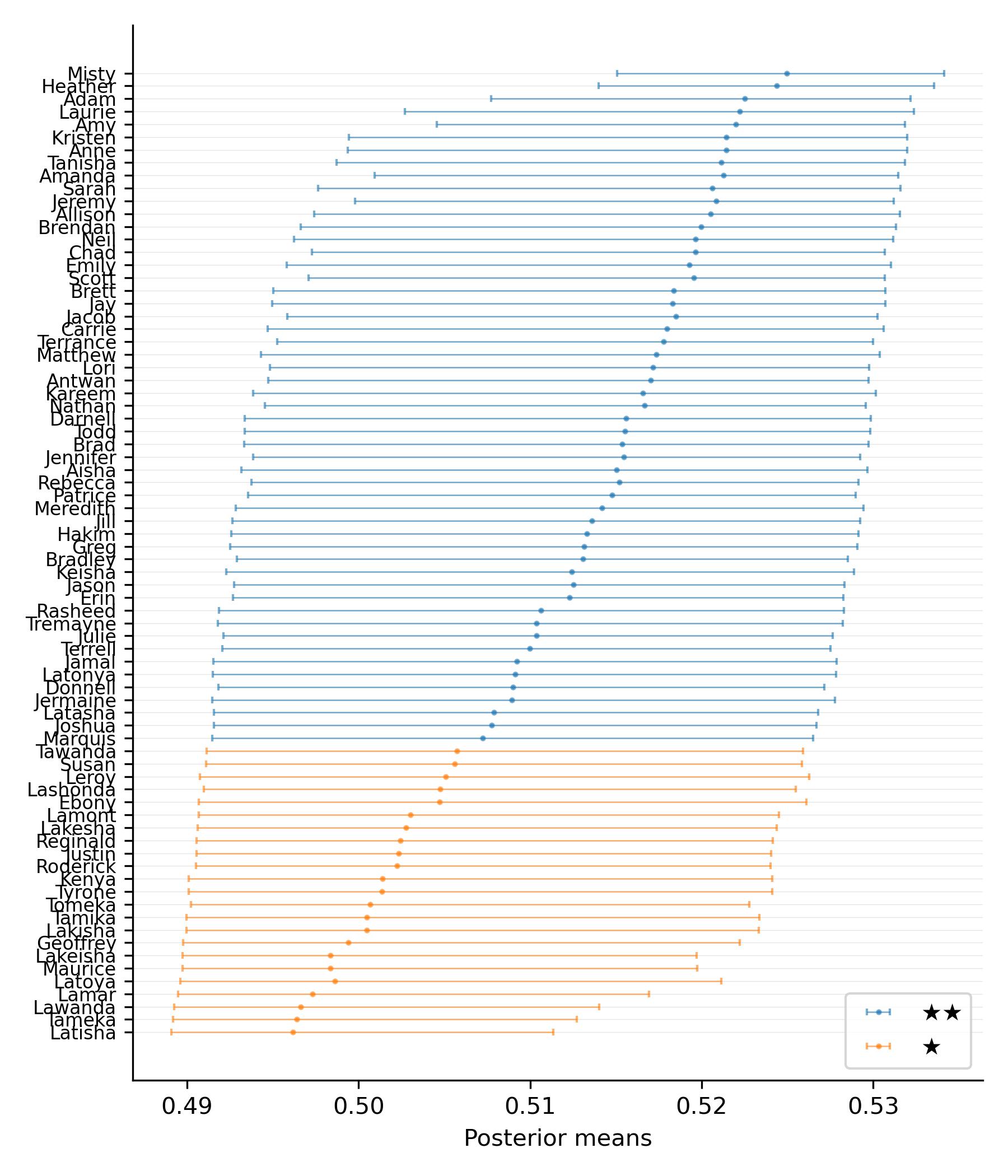
Finally, we provide functionality to plot grades along with posterior means and credible intervals:
from drrank import fig_ranks
# Merge the results with the identity of our observations
results['firstname'] = data.firstname
fig_ranks(ranking = results, posterior_features = G.posterior_df, ylabels = 'firstname', ylabel_fontsize = 8, save_path = 'example/name_ranking.jpg')
Within the function you can specify the following arguments:
- results: ranking results from drrank.fit
- posterior_features: posterior features computed through G.compute_posteriors()
- ylabels: optional, specify the column in results where we have stored the labels of each observation (default =
None) - ylabel_fontsize: optional, specify font size for labels (default = 8)
- show_plot: whether to show the plot or not (default =
True) - save_path: path to where the plot will be saved;
Noneimplies the graph will not be saved (default =None)
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file drrank-0.1.3.tar.gz.
File metadata
- Download URL: drrank-0.1.3.tar.gz
- Upload date:
- Size: 16.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.9.12
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ef7cb1b7c0e6068c2b08fd5a08e1072e36fa4173e8d6c81b9329eda4e2719c6b |
|
| MD5 | 56a79846010ed40f573b8fe226ae6716 |
|
| BLAKE2b-256 | 32cf2cd27389060f4326f6bdb18134aee5bcc33161339654598aa50a35819fdf |
File details
Details for the file drrank-0.1.3-py3-none-any.whl.
File metadata
- Download URL: drrank-0.1.3-py3-none-any.whl
- Upload date:
- Size: 18.4 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.9.12
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 7a6ef0c8f029913224ad720bab6dca83c2a023c3b47c60a9a358b0bad5991b05 |
|
| MD5 | c8edae9820f036f38eee39c2db9847f4 |
|
| BLAKE2b-256 | 577e7498a051beda0137f01fa21ab5eee3981a91cb75c73d2e3678ea39cff1dd |