felupe 7.0.0

Finite Element Analysis

🔍 FElupe - Finite Element Analysis

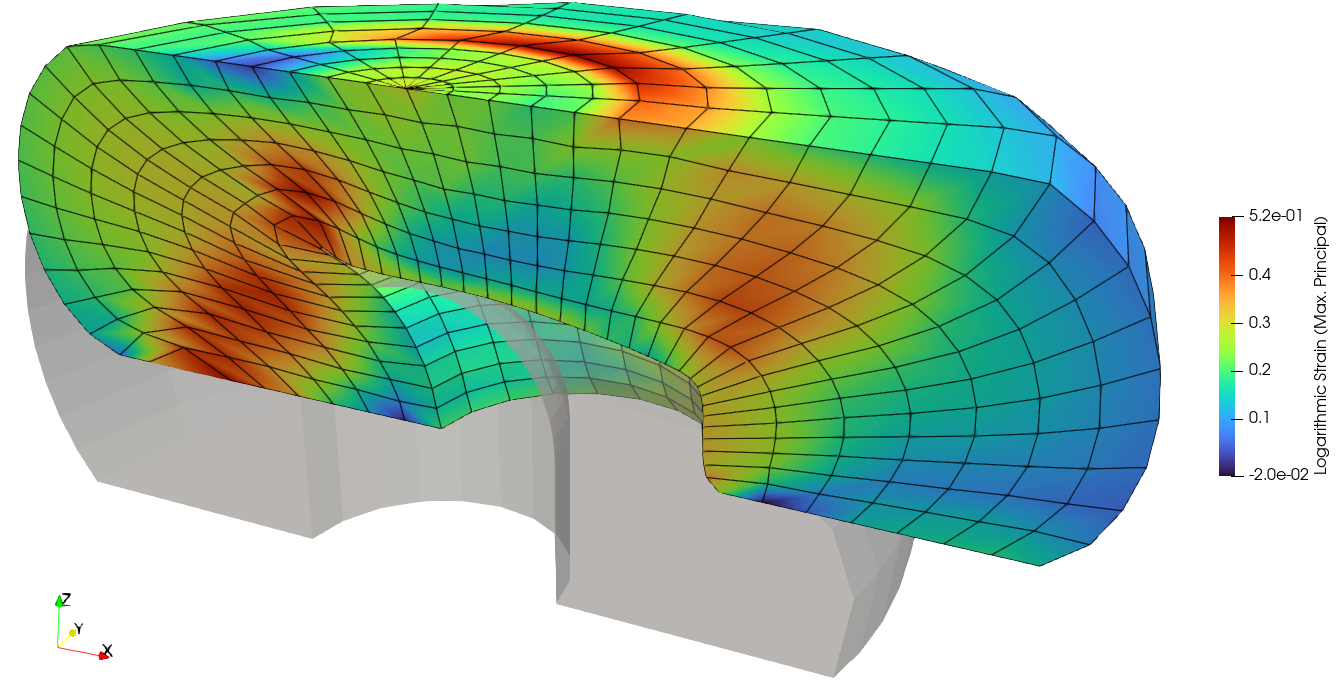
FElupe is a Python 3.7+ finite element analysis package focussing on the formulation and numerical solution of nonlinear problems in continuum mechanics of solid bodies. Its name is a combination of FE (finite element) and the german word Lupe (magnifying glass) as a synonym for getting an insight how a finite element analysis code looks like under the hood.

Installation

Install Python, fire up a terminal and run

pip install felupe[all]

where [all] installs all optional dependencies. By default, FElupe depends on numpy, scipy and einsumt. In order to make use of all features of FElupe, it is suggested to install all optional dependencies (h5py, meshio and tensortrax).

Getting Started

A quarter model of a solid cube with hyperelastic material behaviour is subjected to a uniaxial elongation applied at a clamped end-face. This involves the creation of a mesh, a region as well as a displacement field (encapsulated in a field container). Furthermore, the boundary conditions are created by a template for a uniaxial loadcase. An isotropic pseudo-elastic Ogden-Roxburgh Mullins-softening model formulation in combination with an isotropic hyperelastic Neo-Hookean material formulation is applied on a nearly-incompressible solid body. A step generates the consecutive substep-movements of a given boundary condition. The step is further added to a list of steps of a job (here, a characteristic-curve job is used). During evaluation, each substep of each step is solved by an iterative Newton-Rhapson procedure. The solution is exported after each completed substep as a time-series XDMF file. For more details beside this high-level code snippet, please have a look at the documentation.

import felupe as fem

# create a hexahedron-region on a cube
mesh = fem.Cube(n=11)
region = fem.RegionHexahedron(mesh)

# add a field container (with a vector-valued displacement field)
field = fem.FieldContainer([fem.Field(region, dim=3)])

# apply a uniaxial elongation on the cube
boundaries = fem.dof.uniaxial(field, clamped=True)[0]

# define the constitutive material behaviour
# and create a nearly-incompressible (u,p,J - formulation) solid body
umat = fem.OgdenRoxburgh(material=fem.NeoHooke(mu=1), r=3, m=1, beta=0)
solid = fem.SolidBodyNearlyIncompressible(umat, field, bulk=5000)

# prepare a step with substeps
move = fem.math.linsteps([0, 2, 0], num=10)
step = fem.Step(items=[solid], ramp={boundaries["move"]: move}, boundaries=boundaries)

# add the step to a job, evaluate all substeps and create a plot
job = fem.CharacteristicCurve(steps=[step], boundary=boundaries["move"])
job.evaluate(filename="result.xdmf")
fig, ax = job.plot(
    xlabel="Displacement $u$ in mm $\longrightarrow$",
    ylabel="Normal Force $F$ in N $\longrightarrow$",
)

https://user-images.githubusercontent.com/5793153/200951381-ea310e54-7623-4dd1-a55f-a28f9055063f.mp4

Documentation

The documentation is located here.

Extension Packages

The capabilities of FElupe may be enhanced with extension packages created by the community.

Package	Description	Link
tensortrax	Math on (Hyper-Dual) Tensors with Trailing Axes	https://github.com/adtzlr/tensortrax
matADi	Material Definition with Automatic Differentiation (AD)	https://github.com/adtzlr/matadi
FEplot	A visualization tool for FElupe	https://github.com/ZAARAOUI999/feplot

Changelog

All notable changes to this project will be documented in this file. The format is based on Keep a Changelog, and this project adheres to Semantic Versioning.

License

FElupe - finite element analysis (C) 2023 Andreas Dutzler, Graz (Austria).

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.