A collection of Lambert's problem solvers.
Project description
lamberthub: a hub of Lambert's problem solvers
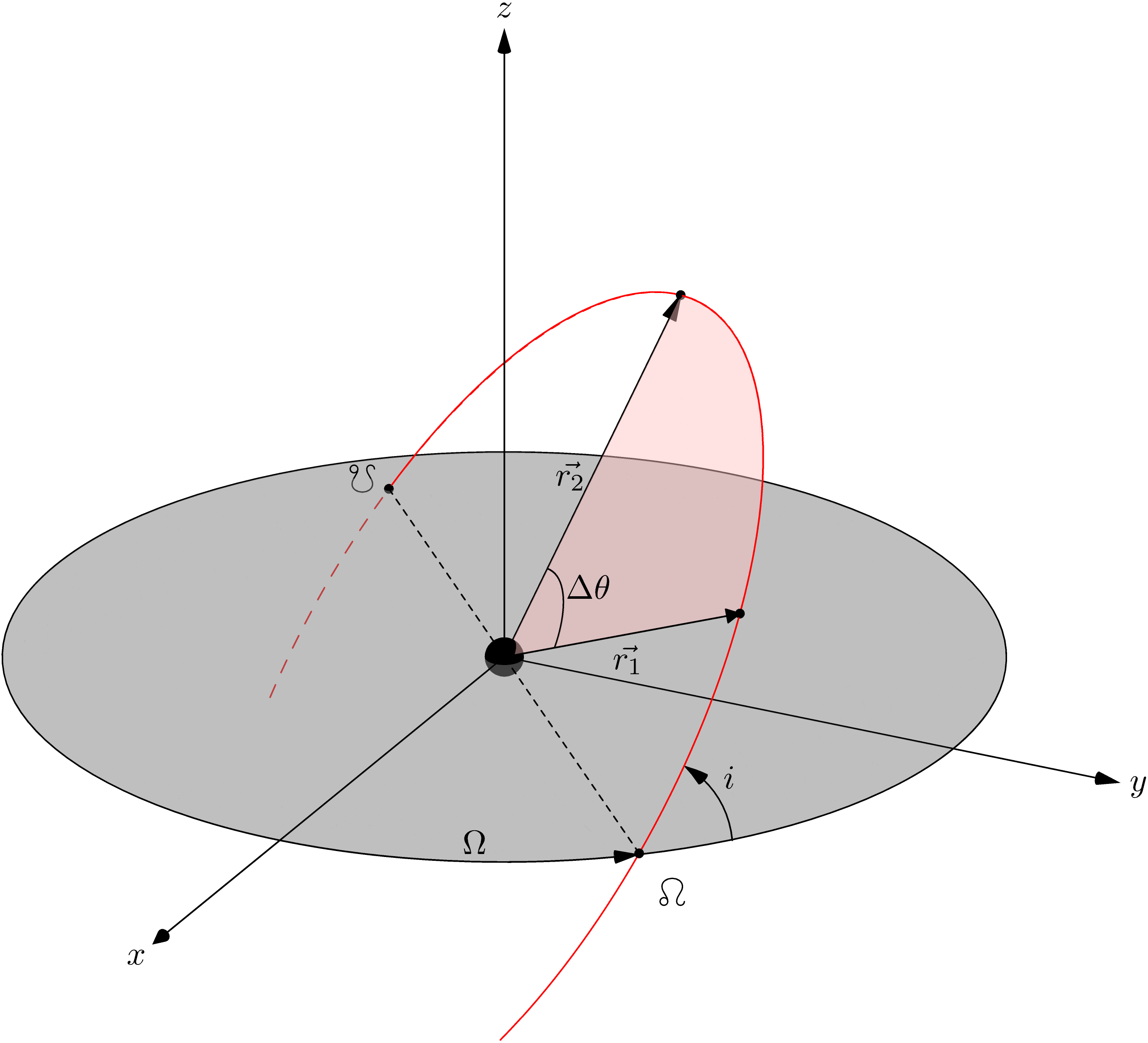
A Python library designed to provide solutions to Lambert's problem, a classical problem in astrodynamics that involves determining the orbit of a spacecraft given two points in space and the time of flight between them. The problem is essential for trajectory planning, particularly for interplanetary missions.
Lamberthub implements multiple algorithms, each named after its author and publication year, for solving different variations of Lambert's problem. These algorithms can handle different types of orbits, including multi-revolution paths and direct transfers.
Installation
Install lamberthub by running:
python -m pip install lamberthub
Available solvers
| Algorithm | Reference |
|---|---|
gauss1809 |
C. F. Gauss, Theoria motus corporum coelestium in sectionibus conicis solem ambientium. 1809. |
battin1984 |
R. H. Battin and R. M. Vaughan, “An elegant lambert algorithm,” Journal of Guidance, Control, and Dynamics, vol. 7, no. 6, pp. 662–670, 1984. |
gooding1990 |
R. Gooding, “A procedure for the solution of lambert’s orbital boundary-value problem,” Celestial Mechanics and Dynamical Astronomy, vol. 48, no. 2, pp. 145–165, 1990. |
avanzini2008 |
G. Avanzini, “A simple lambert algorithm,” Journal of Guidance, Control, and Dynamics, vol. 31, no. 6, pp. 1587–1594, 2008. |
arora2013 |
N. Arora and R. P. Russell, “A fast and robust multiple revolution lambert algorithm using a cosine transformation,” Paper AAS, vol. 13, p. 728, 2013. |
vallado2013 |
D. A. Vallado, Fundamentals of astrodynamics and applications. Springer Science & Business Media, 2013, vol. 12. |
izzo2015 |
D. Izzo, “Revisiting lambert’s problem,” Celestial Mechanics and Dynamical Astronomy, vol. 121, no. 1, pp. 1–15, 2015. |
Using a solver
Any Lambert's problem algorithm implemented in lamberthub is a Python function
which accepts the following parameters:
from lamberthub import authorYYYY
v1, v2 = authorYYYY(
mu, r1, r2, tof, M=0, prograde=True, low_path=True, # Type of solution
maxiter=35, atol=1e-5, rtol=1e-7, full_output=False # Iteration config
)
where author is the name of the author which developed the solver and YYYY
the year of publication. Any of the solvers hosted by the ALL_SOLVERS list.
Parameters and Returns
| Parameters | Description |
|---|---|
mu |
The gravitational parameter, i.e., mass of the attracting body times the gravitational constant. Equivalent to gravitational constant times the mass of the attractor body. |
r1 |
Initial position vector. |
r2 |
Final position vector. |
tof |
Time of flight between initial and final vectors. |
M |
The number of revolutions. If zero (default), direct transfer is assumed. |
prograde |
Controls the inclination of the final orbit. If True, inclination between 0 and 90 degrees. If False, inclination between 90 and 180 degrees. |
low_path |
Selects the type of path when more than two solutions are available. No specific advantage unless there are mission constraints. |
maxiter |
Maximum number of iterations allowed when computing the solution. |
atol |
Absolute tolerance for the iterative method. |
rtol |
Relative tolerance for the iterative method. |
full_output |
If True, returns additional information such as the number of iterations. |
| Returns | Description |
|---|---|
v1 |
Initial velocity vector. |
v2 |
Final velocity vector. |
numiter |
Number of iterations (only if full_output is True). |
tpi |
Time per iteration (only if full_output is True). |
Examples
Example: solving for a direct and prograde transfer orbit
Problem statement
Suppose you want to solve for the orbit of an interplanetary vehicle (that is Sun is the main attractor) form which you know that the initial and final positions are given by:
\vec{r_1} = \begin{bmatrix} 0.159321004 \\ 0.579266185 \\ 0.052359607 \end{bmatrix} \text{ [AU]} \quad \quad
\vec{r_2} = \begin{bmatrix} 0.057594337 \\ 0.605750797 \\ 0.068345246 \end{bmatrix} \text{ [AU]} \quad \quad
The time of flight is $\Delta t = 0.010794065$ years. The orbit is
prograde and direct, thus $M=0$. Remember that when $M=0$, there is only one
possible solution, so the low_path flag does not play any role in this
problem.
Solution
For this problem, gooding1990 is used. Any other solver would work too. Next,
the parameters of the problem are instantiated. Finally, the initial and final
velocity vectors are computed.
from lamberthub import gooding1990
import numpy as np
mu_sun = 39.47692641
r1 = np.array([0.159321004, 0.579266185, 0.052359607])
r2 = np.array([0.057594337, 0.605750797, 0.068345246])
tof = 0.010794065
v1, v2 = gooding1990(mu_sun, r1, r2, tof, M=0, prograde=True)
print(f"Initial velocity: {v1} [AU / years]")
print(f"Final velocity: {v2} [AU / years]")
Result
Initial velocity: [-9.303608 3.01862016 1.53636008] [AU / years]
Final velocity: [-9.511186 1.88884006 1.42137810] [AU / years]
Directly taken from An Introduction to the Mathematics and Methods of Astrodynamics, revised edition, by R.H. Battin, problem 7-12.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Hashes for lamberthub-1.0.0a1-py3-none-any.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 104f2eb369b1f5e34f8e16737dd11fd02890396ed7c498c2bc01dd9858bf0e04 |
|
| MD5 | f9e909c3b189531a4276d1a9ca6f7496 |
|
| BLAKE2b-256 | 01695e606a5fa494f45d6c56a1f28e1ffc169d46d5cfd40fc7ce70cc3200fb72 |

















