A package that provides a kinematic analysis of mechanisms, cams, and gears.
Project description
Purpose
This package was created to aid with the designing process of mechanisms involving linkages, cams, and gears. In regard to linkages, it is capable of implementing a kinematic analysis with the knowledge of the degrees of freedom for the vectors that make up the mechanism. With the aid of numerical solving and iteration, the position, velocity, and acceleration of these vectors and points may be acquired.
In regard to cams, this package is capable of supplying coordinates of a cam profile, plotting SVAJ diagrams, and getting a cam and follower animation for roller and flat faced followers. In turn, the coordinates may be supplied to a machinist or imported into SolidWorks. All that is needed to know is the motion description (i.e. rise 2 inches in 1 second, dwell for 1.5 seconds, fall 2 inches in 3 seconds). As of right now, the kinds of motion supported are naive/uniform motion (how the cam shouldn't be designed), harmonic motion, and cycloidal motion. It is possible that this gets updated in the future with better options such as modified sinusoidal motion.
Gears are not yet supported for this package. The goal in the future is to be able to design a custom gear by knowing properties of an involute gear tooth. Similarly to the cam profile, the coordinates could be extracted.
Results/Examples
fourbarlinkage.py
crunode_coupler.py
crankslider.py
engine.py
non_grashof.py
cam2_example.py
Linkages, Cranks, Couplers, and Rockers
In order to use the contents of mechanism.py, a basic knowledge of vector loops must be known. The structure of the
vector loops function is shown in several files under the examples folder. To gain a greater understanding of this
package's usage, this walk through is provided.
Four Bar Linkage Example
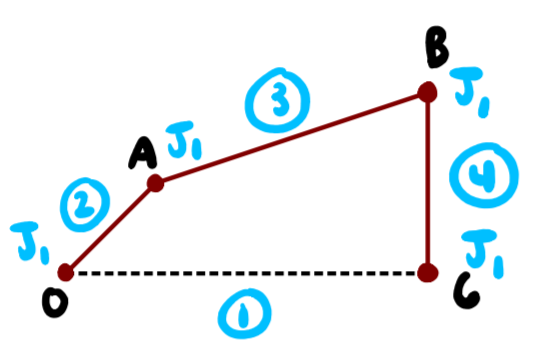
A four bar linkage is the basic building block of all mechanisms. This is similar to how the triangle is the basic building block of all structures. What defines a mechanism or structure is the system's overall number of degrees of freedom, and the number of degrees of freedom is determined via Kutzbach’s equation.
Kutzbach's equation is: total degrees of freedom = 3(#links - 1) - 2(J1) - J2 where J1 is the number of full joints (also known as a revolute joint) and J2 is the number of half joints. For this four bar linkage, there are 4 full joints.
The number of degrees of freedom is: 3(4 - 1) - 2(4) = 1
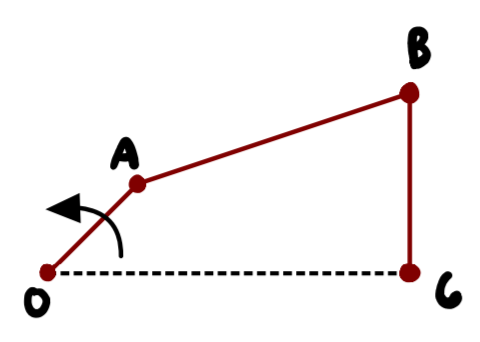
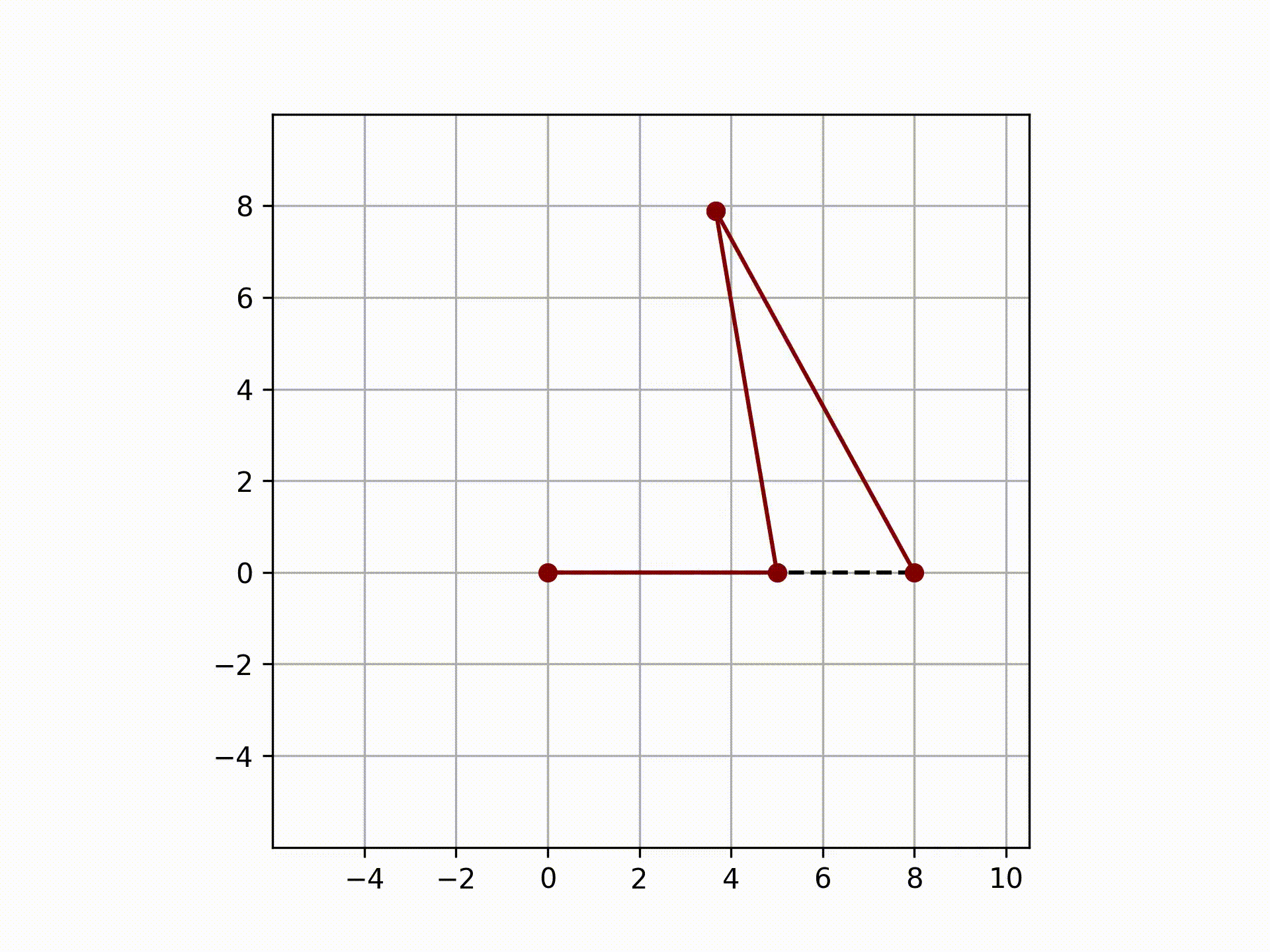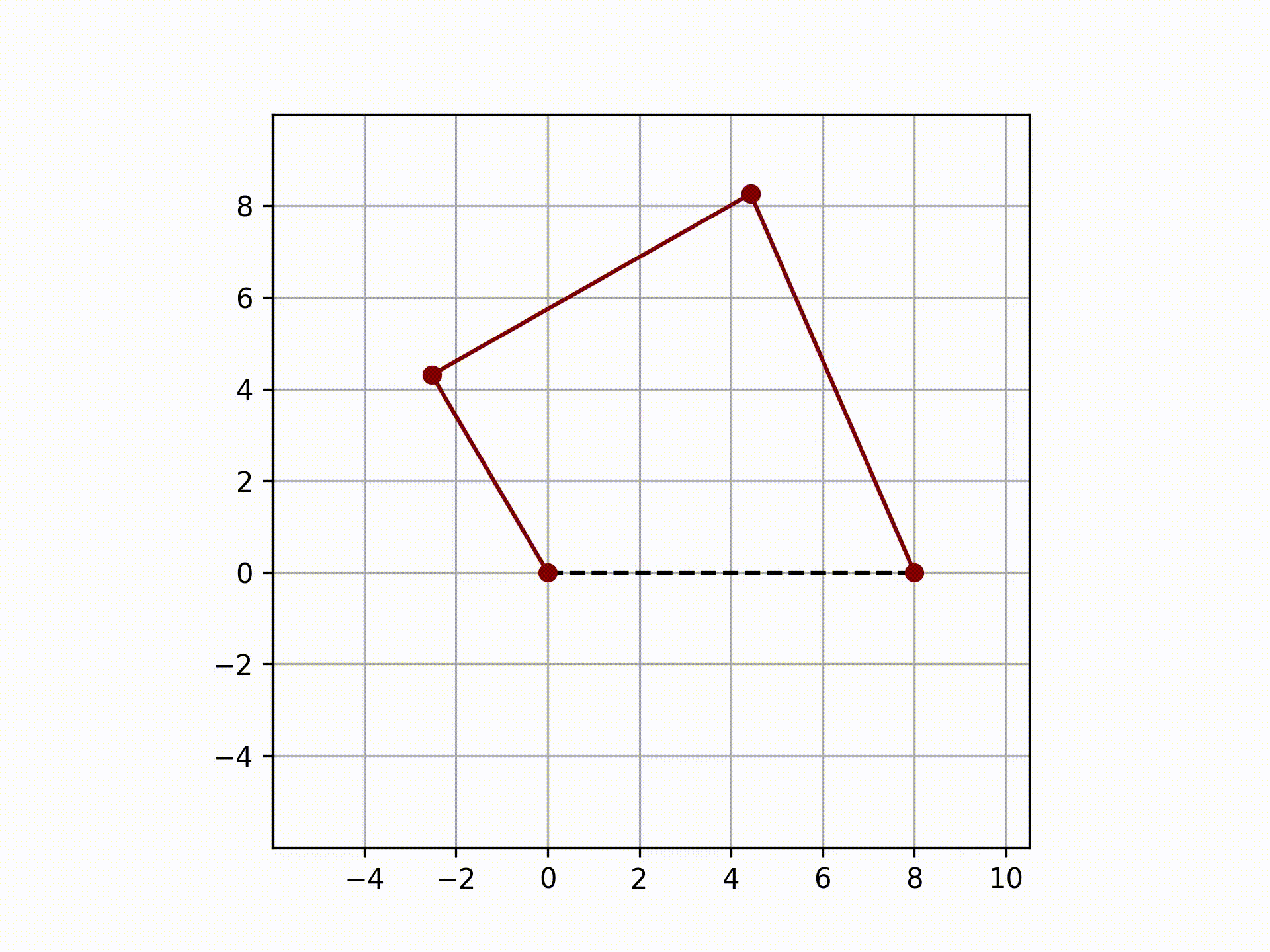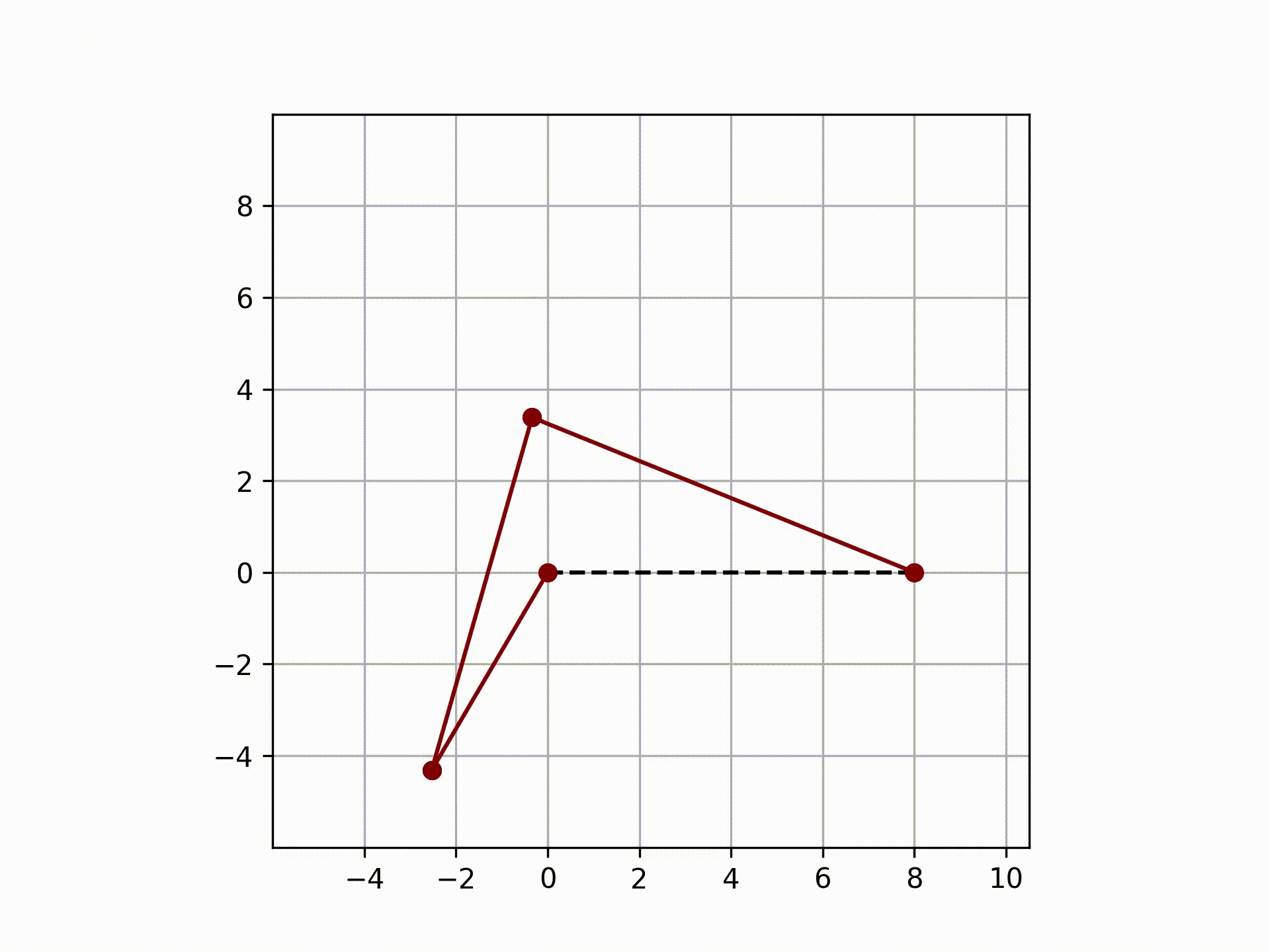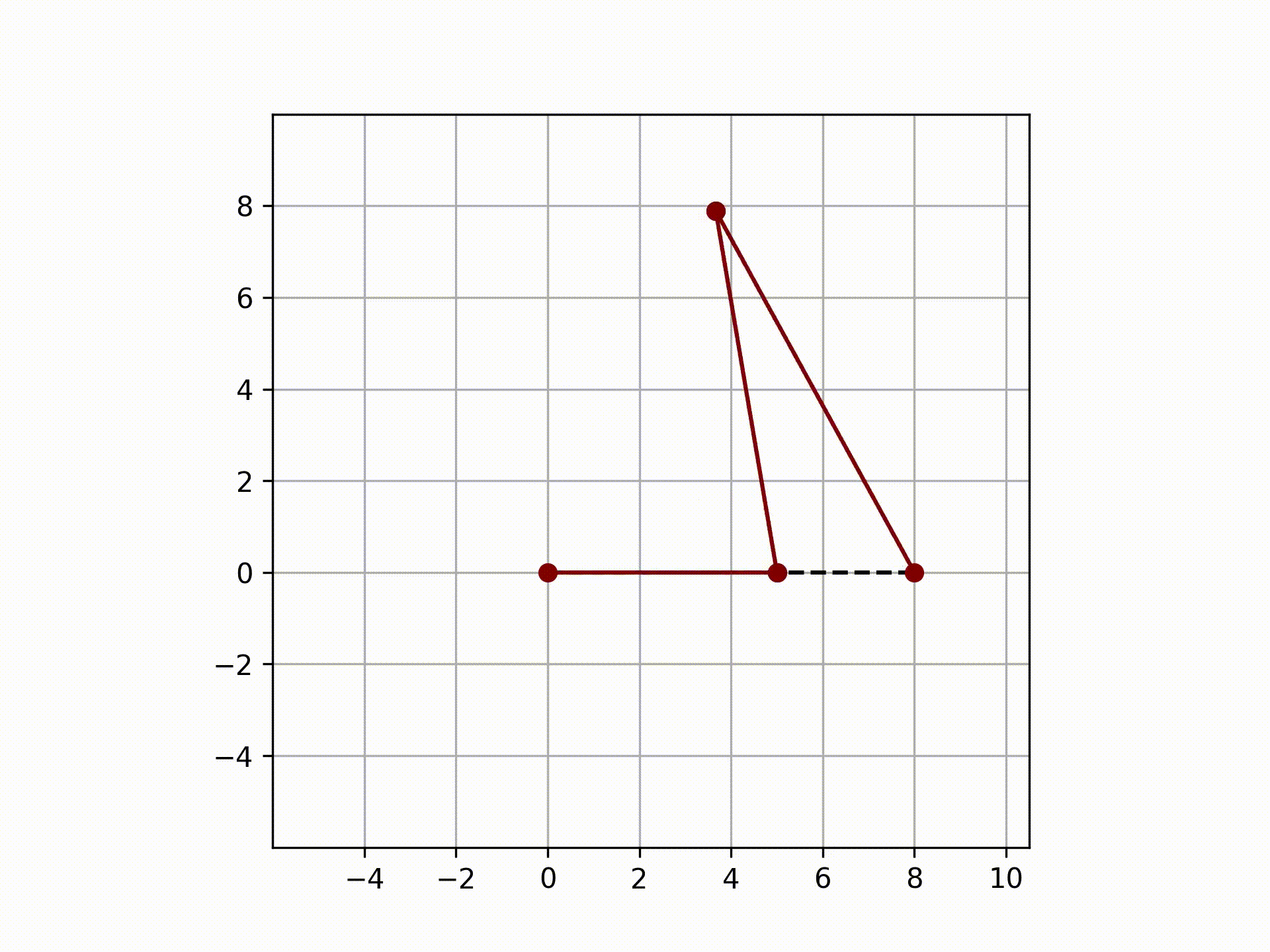
This means that we need one known input to find the unknowns of the system. This can be explained further with a diagram of the vectors that make up the four bar linkage.
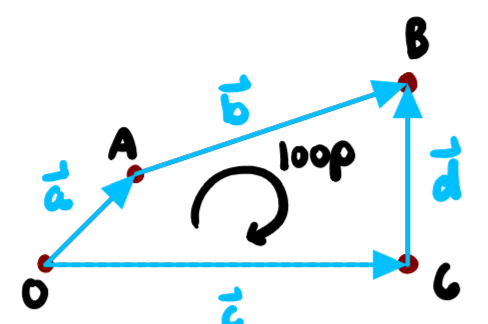
From the above image, the vector "a" is the crank. The speed at which it rotates will be considered as the input to the system, and thus, it is the defining parameter to the system.
The lengths of all the vectors are known. The only two unknowns are the angle that corresponds to vector "b" and "d". It is important to note that the objects that make up this package are vectors, and the polar form of the vectors is the main interest.
There is only one loop equation which provides two equations when breaking down the vectors into its components. With two equations and two unknowns, this system becomes solvable.
Problem Statement
Consider the four bar linkage shown above. The lengths of a, b, c, and d are 5", 8", 8" and 9". The crank (a) rotates at
a constant 500 RPM. Use mechanism to get an animation of this linkage system and plot the angles, angular velocity,
and angular acceleration of vector d as a function of time.
Solution
The four bar linkage is a grashof linkage because it satisfies the grashof condition (9 + 5 < 8 + 8). This means that the crank is able to fully rotate. The input can be deduced by integrating and differentiating the constant value of the constant angular velocity of the crank.
Always begin with defining the joints and vectors.
from mechanism import *
import numpy as np
import matplotlib.pyplot as plt
# Declare the joints that make up the system.
O, A, B, C = get_joints('O A B C')
# Declare the vectors and keep in mind that angles are in radians and start from the positive x-axis.
a = Vector((O, A), r=5)
b = Vector((A, B), r=8)
c = Vector((O, C), r=8, theta=0, style='ground')
d = Vector((C, B), r=9)
Always define the vectors in the polar form. The first argument is the joints, and the first joint is the tail of the vector, and the second is the head. Additionally, extra keyword arguments will be passed to plt.plot() for styling. There should be half as many loop equations as there are unknown. The input vector "a" does not need to have its known values at its declaration. The next thing to do is to define the known input and guesses for the first iteration of the unknown values.
# Define the known input to the system.
# For a 500 RMP crank, the time it takes to rotate one rev is 0.12s
time = np.linspace(0, 0.12, 300)
angular_velocity = 50*np.pi/3 # This is 500 RPM in rad/s
theta = angular_velocity*time # Integrate to find the theta
omega = np.full((time.size,), angular_velocity) # Just an array of the same angular velocity
alpha = np.zeros(time.size)
# Guess the unknowns
pos_guess = np.deg2rad([45, 90])
vel_guess = np.array([1000, 1000])
acc_guess = np.array([1000, 1000])
The guess values need to be arrays of the same length as the number of unknowns. These arrays will be passed as the first iteration. The next thing to do is to define the loop function and create the mechanism object.
# Define the loop equation(s)
def loop(x, i):
return a(i) + b(x[0]) - c() - d(x[1])
# Create the mechanism object
mechanism = Mechanism(vectors=(a, b, c, d), input_vector=a, loops=loop, pos=theta, vel=omega, acc=alpha,
guess=(pos_guess, vel_guess, acc_guess))
This example is simpler than most others because there is only one loop equation. For multiple loop equations, it is
important that the function returns a flattened array of the same length as there are unknown, and the return array
corresponds to the input guess values. The second argument is the input. It is strongly encouraged to view the examples
for the more rigorous structure of the loop function. The last thing to do is to call mechanism.iterate(), which is
necessary if the input from pos, vel, and acc are arrays. If they are not arrays, then it is assumed that the
mechanism at an instant is desired. If this is the case, then call mechanism.calculate() then call mechanism.plot().
# Call mechanism.iterate() then get and show the animation
mechanism.iterate()
ani = mechanism.get_animation()
# Plot the angles, angular velocity, and angular acceleration of vector d
fig, ax = plt.subplots(nrows=3, ncols=1)
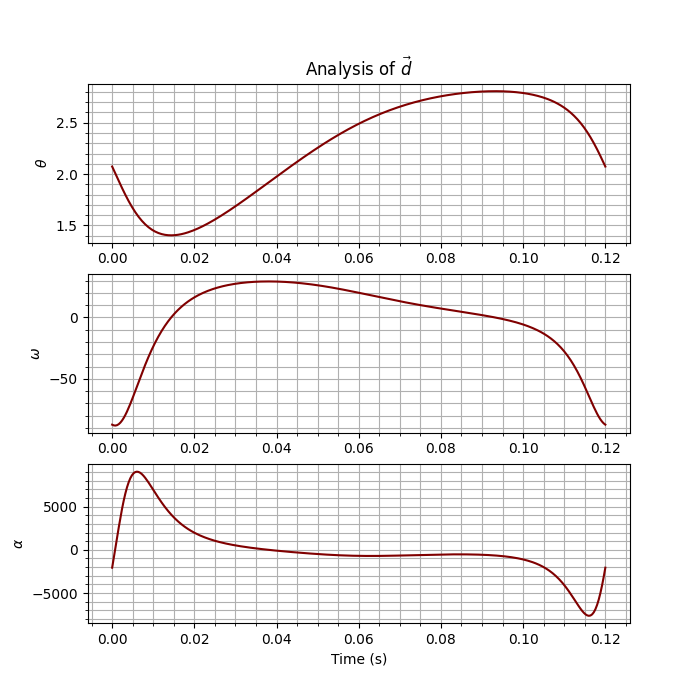
ax[0].plot(time, d.pos.thetas, color='maroon')
ax[1].plot(time, d.vel.omegas, color='maroon')
ax[2].plot(time, d.acc.alphas, color='maroon')
ax[0].set_ylabel(r'$\theta$')
ax[1].set_ylabel(r'$\omega$')
ax[2].set_ylabel(r'$\alpha$')
ax[2].set_xlabel(r'Time (s)')
ax[0].set_title(r'Analysis of $\vec{d}$')
for a in (ax[0], ax[1], ax[2]):
a.minorticks_on()
a.grid(which='both')
fig.set_size_inches(7, 7)
# fig.savefig('../images/analysis_d.png')
plt.show()
This will produce the following output:
Cams
There are several kinds of motion types for a cam, but there is an important corollary when designing cams: The jerk function must be finite across the entire interval (360 degrees) (Robert Norton's Design of Machinery). Usually, the cycloidal motion type achieves this corollary, but it comes at a cost. It produces an acceleration and velocity that is typically higher than the other motion types. More motion types are to come later (hopefully).
Problem Statement
Design a cam using cycloidal motion that has the following motion description:
- Dwell at zero displacement for 90 degrees
- Rise 1 inch in 90 degrees
- Dwell for 90 degrees
- Fall 1 inch in 90 degrees
The cam's angular velocity is 2*pi radians per second. Show the SVAJ diagram as well as the cam's profile. Size the cam for a roller follower with a radius of 1/2" with a maximum pressure angle of 30 degrees. Also size the cam for a flat faced follower using a conservative approach. Get an animation for both a roller/flat faced follower. Finally, save the coordinates of the profile to a text file and show the steps for creating a part in SolidWorks.
Solution
Begin by creating a cam object with the correct motion description.
import numpy as np
from mechanism import Cam
cam = Cam(motion=[
('Dwell', 90),
('Rise', 1, 90),
('Dwell', 90),
('Fall', 1, 90)
], degrees=True, omega=2*np.pi)
The motion description is a list of tuples. Each tuple must contain 3 items for rising and falling and two items for dwelling. The first item of the tuple is a string equal to "Rise", "Fall", or "Dwell" (not case-sensitive). For rise and fall motion, the second item in the tuple is the distance at which the follower falls or rises. For dwelling, the second item in the tuple is either the time (in seconds) or angle (in degrees) for which the displacement remains constant. The third item in the tuple for rising and falling is equivalent to the second item for dwelling. If degrees is set to true, then the last item in each tuple is interpreted as the angle for which the action occurs. A manual input for the angular velocity is then required if conducting further analysis via SVAJ.
This is all that's required to call the following methods.
cam.plot(kind='all')
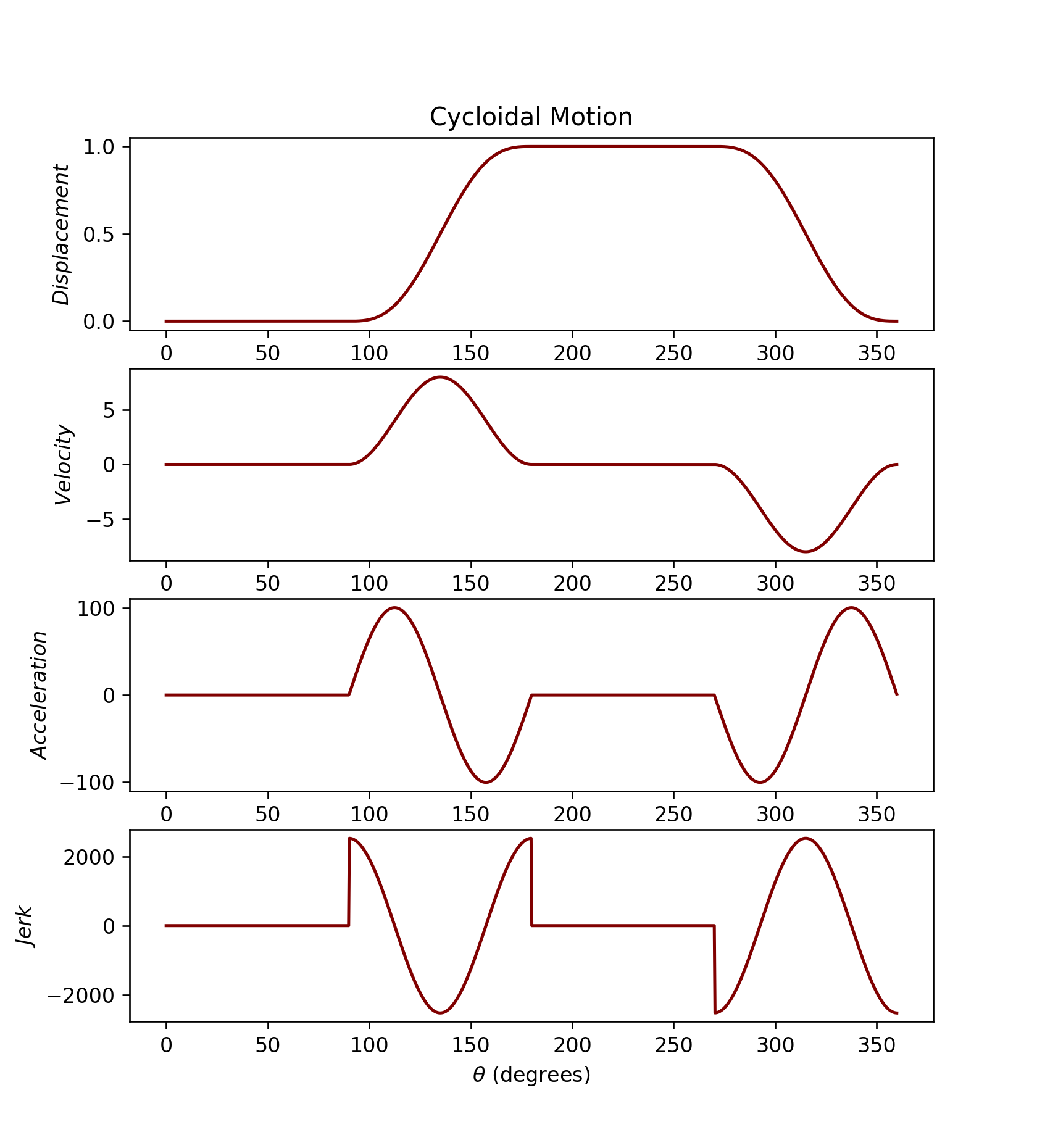
cam.svaj(kind='cycloidal')
This produces the following:
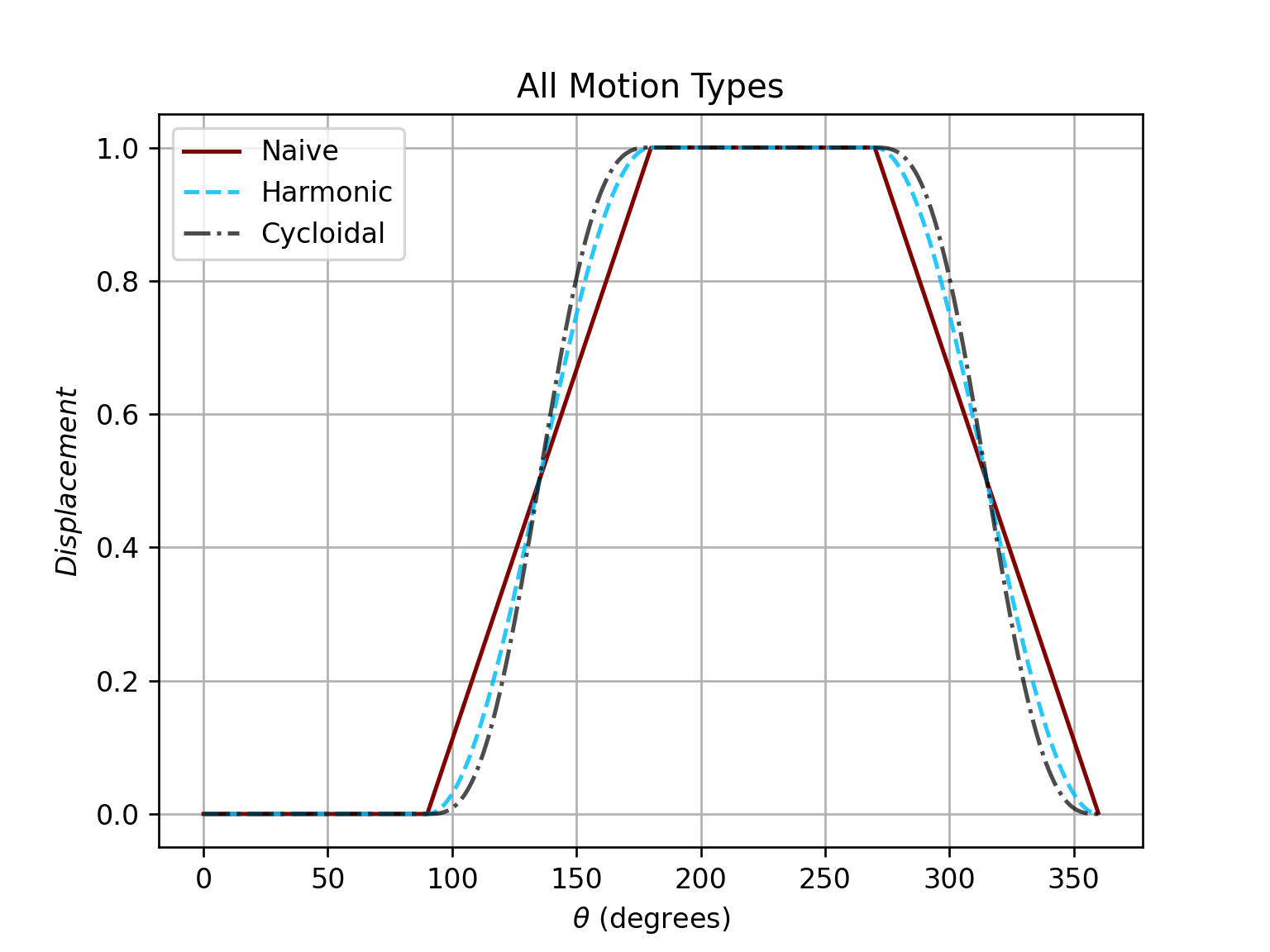
Looking at the acceleration plot, there are no vertical lines. This means that there is no infinite derivative at any instant along the cam's profile; the jerk function is finite across each instant, making this an acceptable motion type.
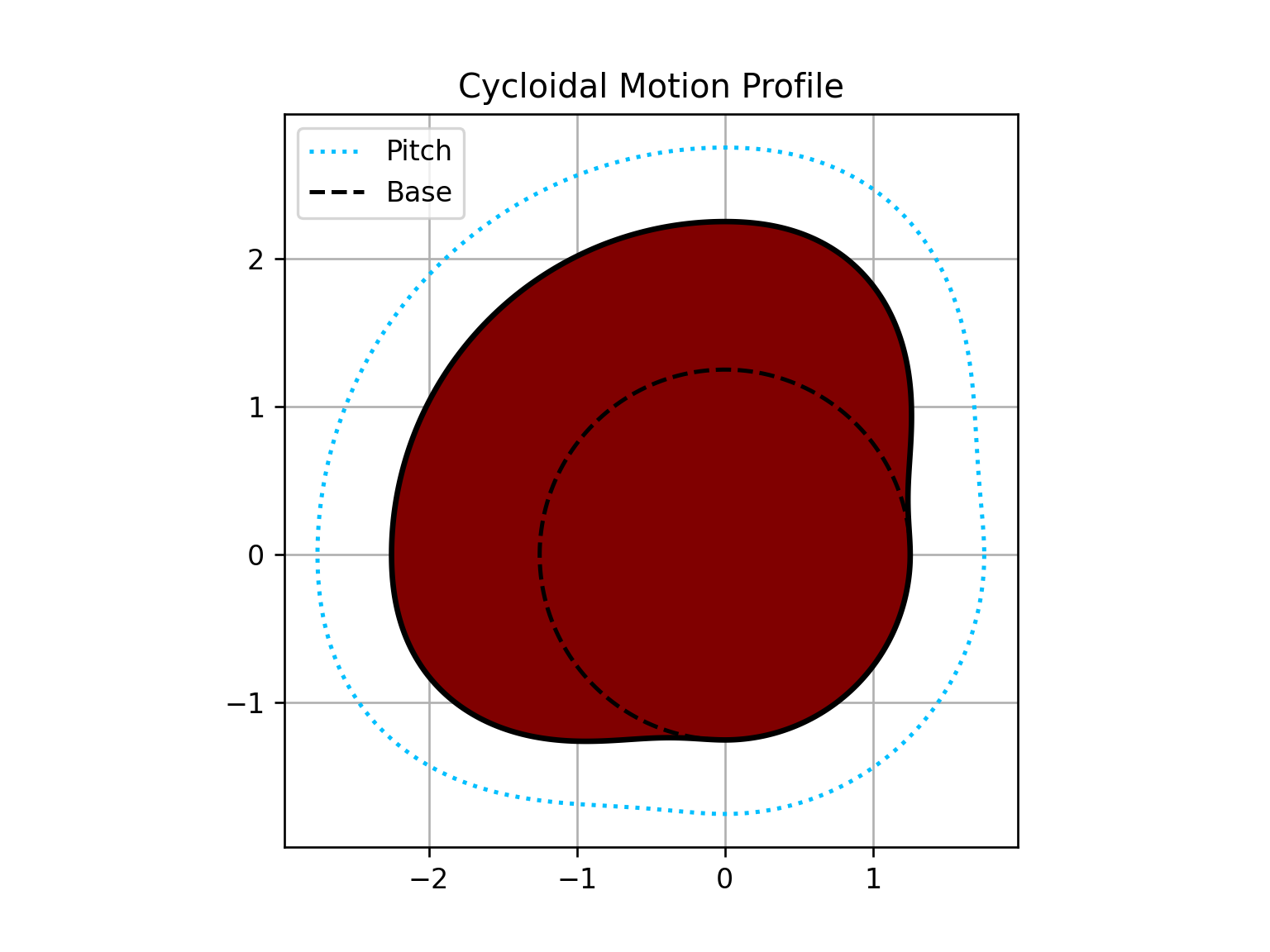
If a roller follower with a 1/2" radius is desired, an analysis depending on the cam's radius of curvature and pressure angle can be conducted to determine the base circle of the cam.
roller_analysis = cam.get_base_circle(kind='cycloidal', follower='roller', roller_radius=1/2, max_pressure_angle=30,
plot=True)
cam.profile(kind='cycloidal', base=roller_analysis['Rb'], show_base=True, roller_radius=1/2, show_pitch=True,
loc='best')
Output:
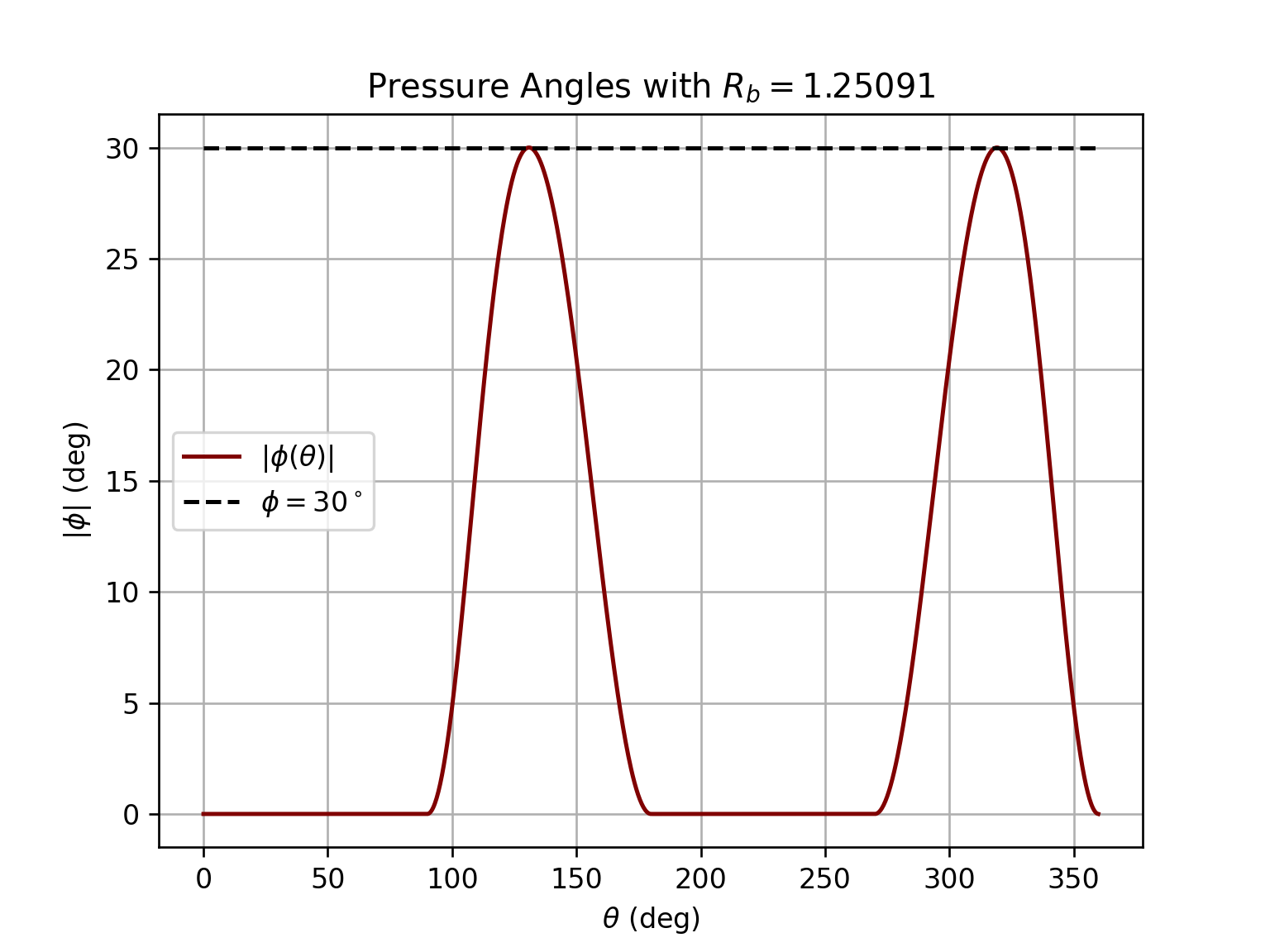
For a flat faced follower, the radius of curvature at the point of contact should be positive (or greater than 0.25") for all theta. There is an option to return the base radius such that the radius of curvature of the cam's profile is positive for all values of theta (this is the conservative approach).
flat_analysis = cam.get_base_circle(kind='cycloidal', follower='flat', desired_min_rho=0.25, conservative_flat=True)
print(flat_analysis['Rb'])
print(flat_analysis['Min Face Width'])
cam.profile(kind='cycloidal', base=flat_analysis['Rb'], show_base=True)
Output:
The base circle radius using the conservative approach is 2.21 and the minimum face width for the follower was found to be 2.55"
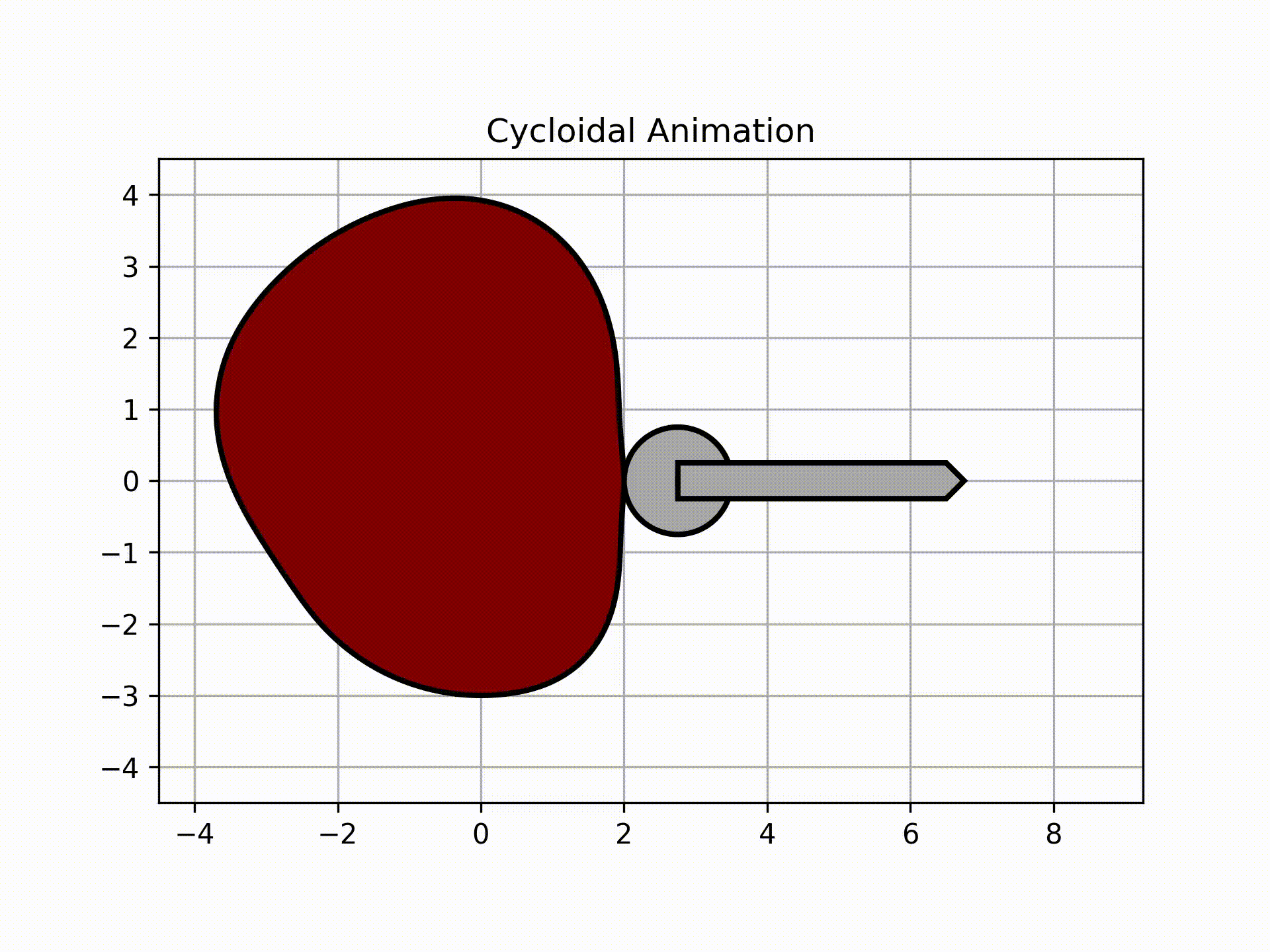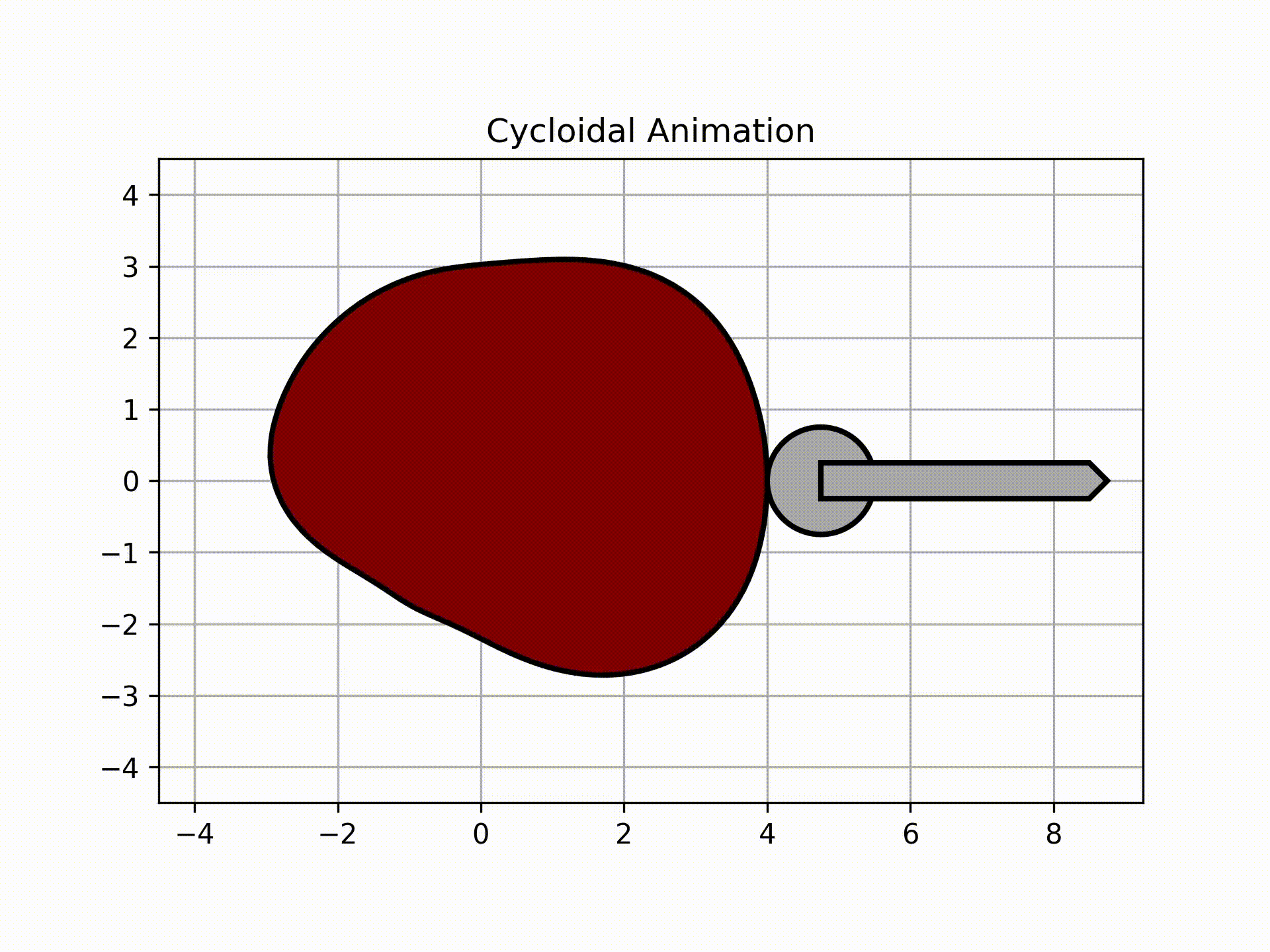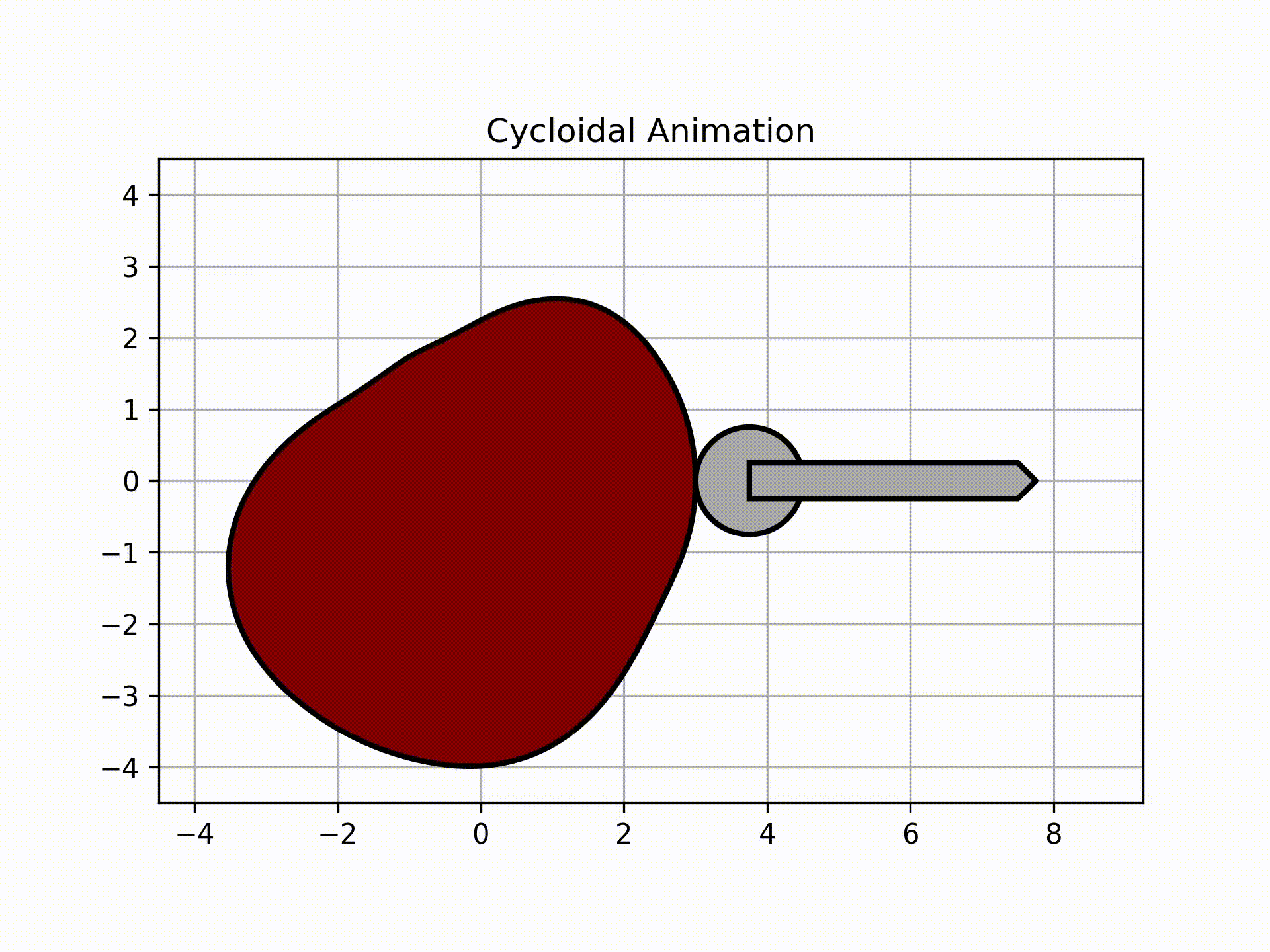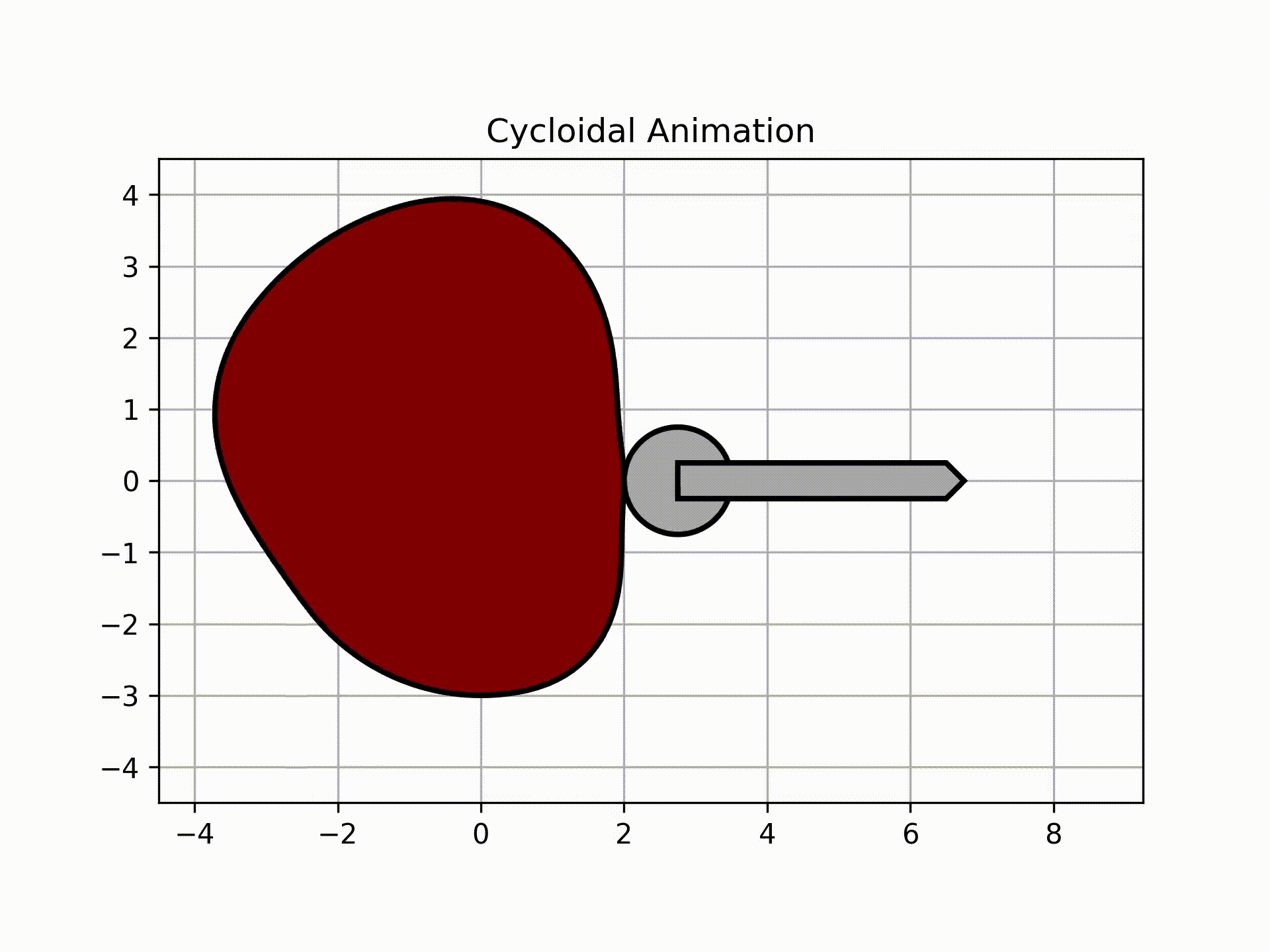
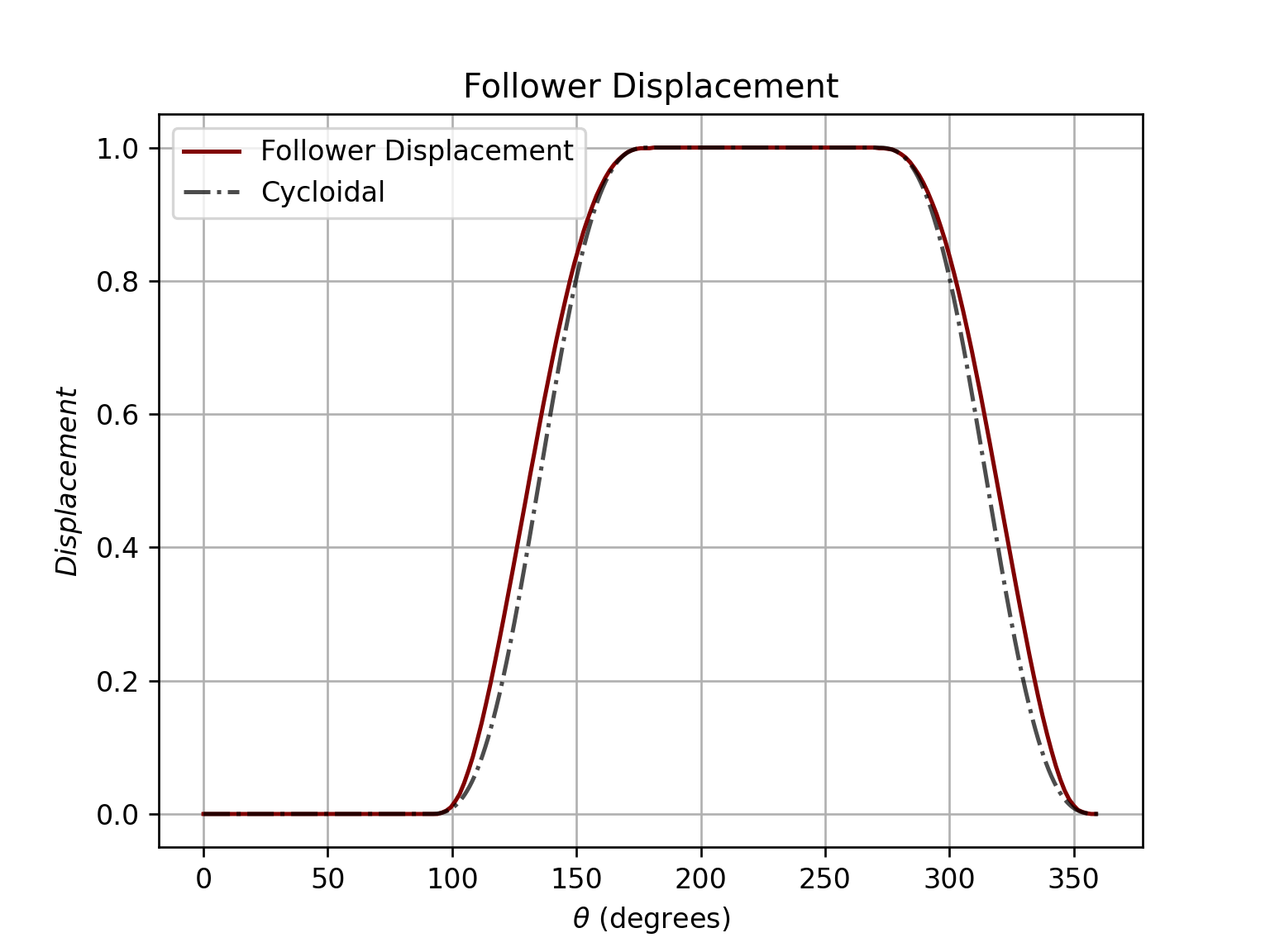
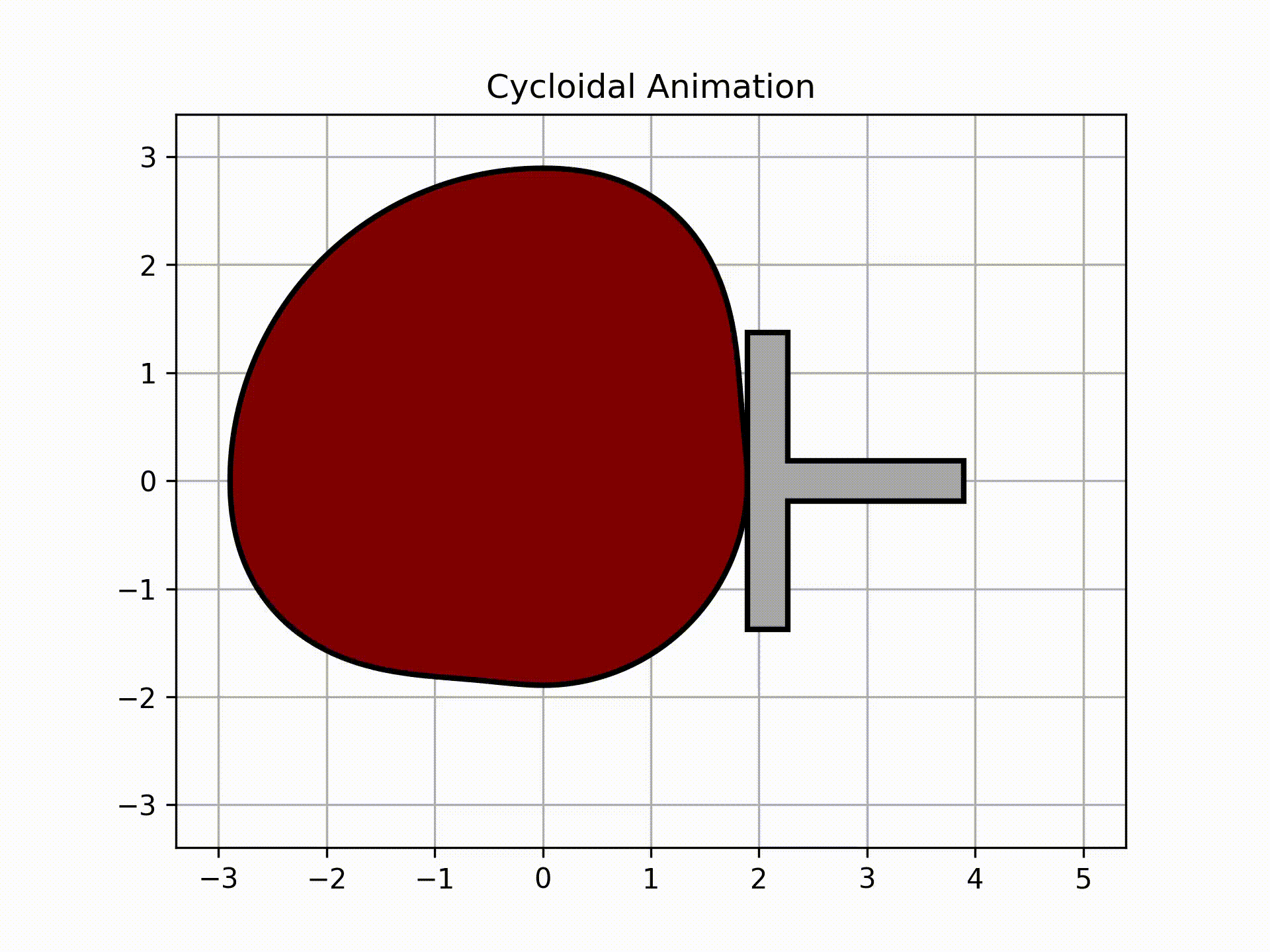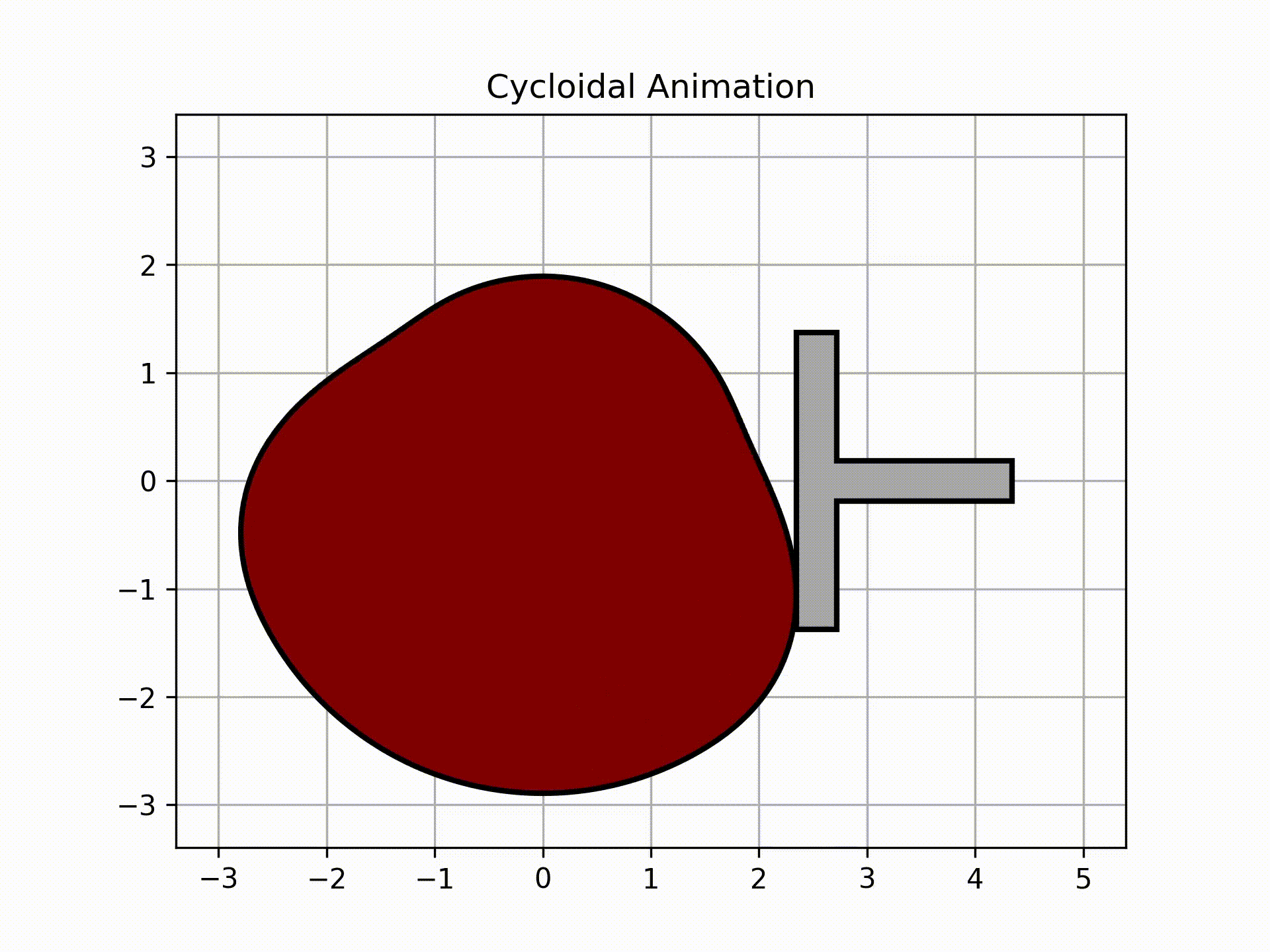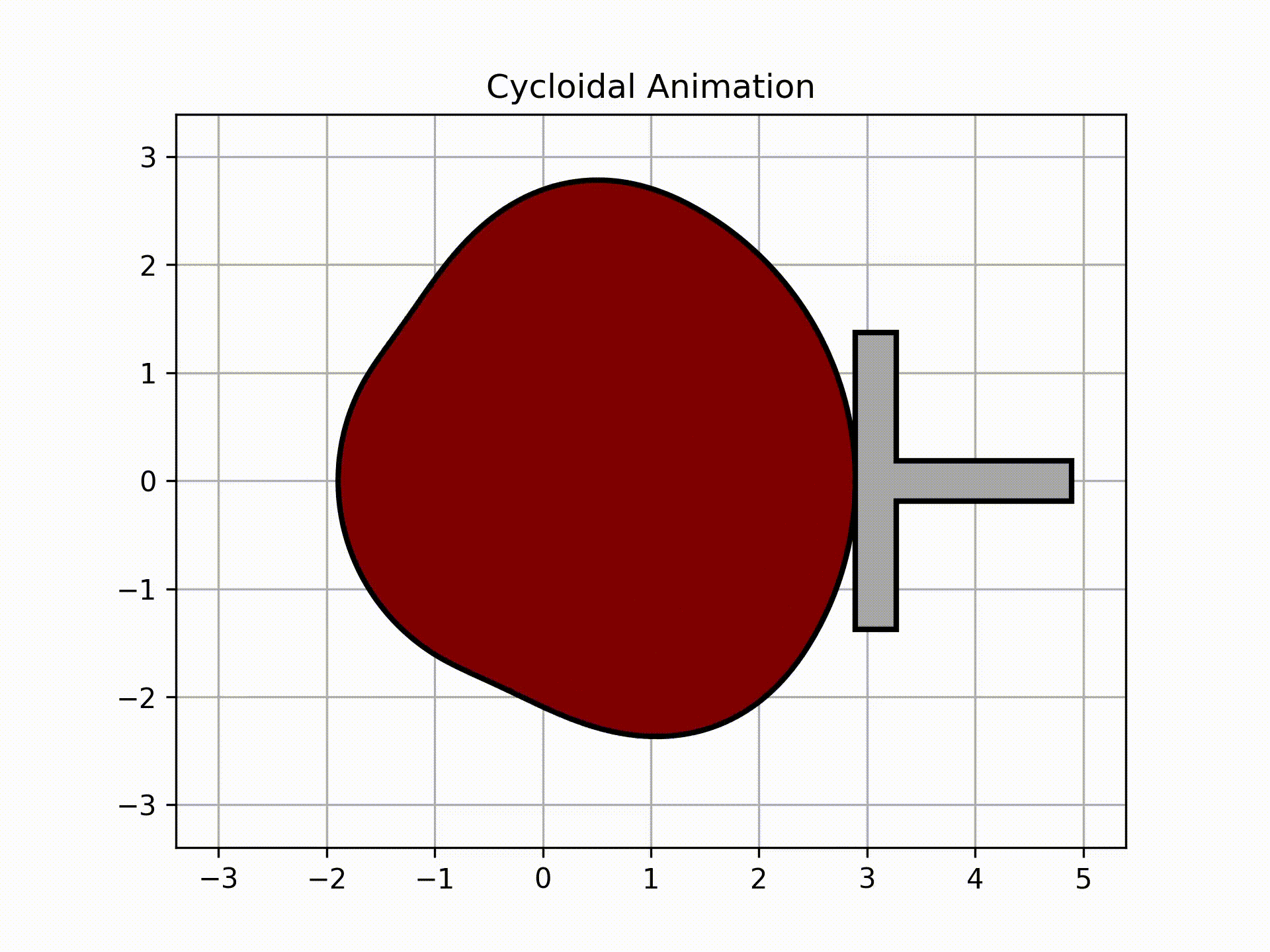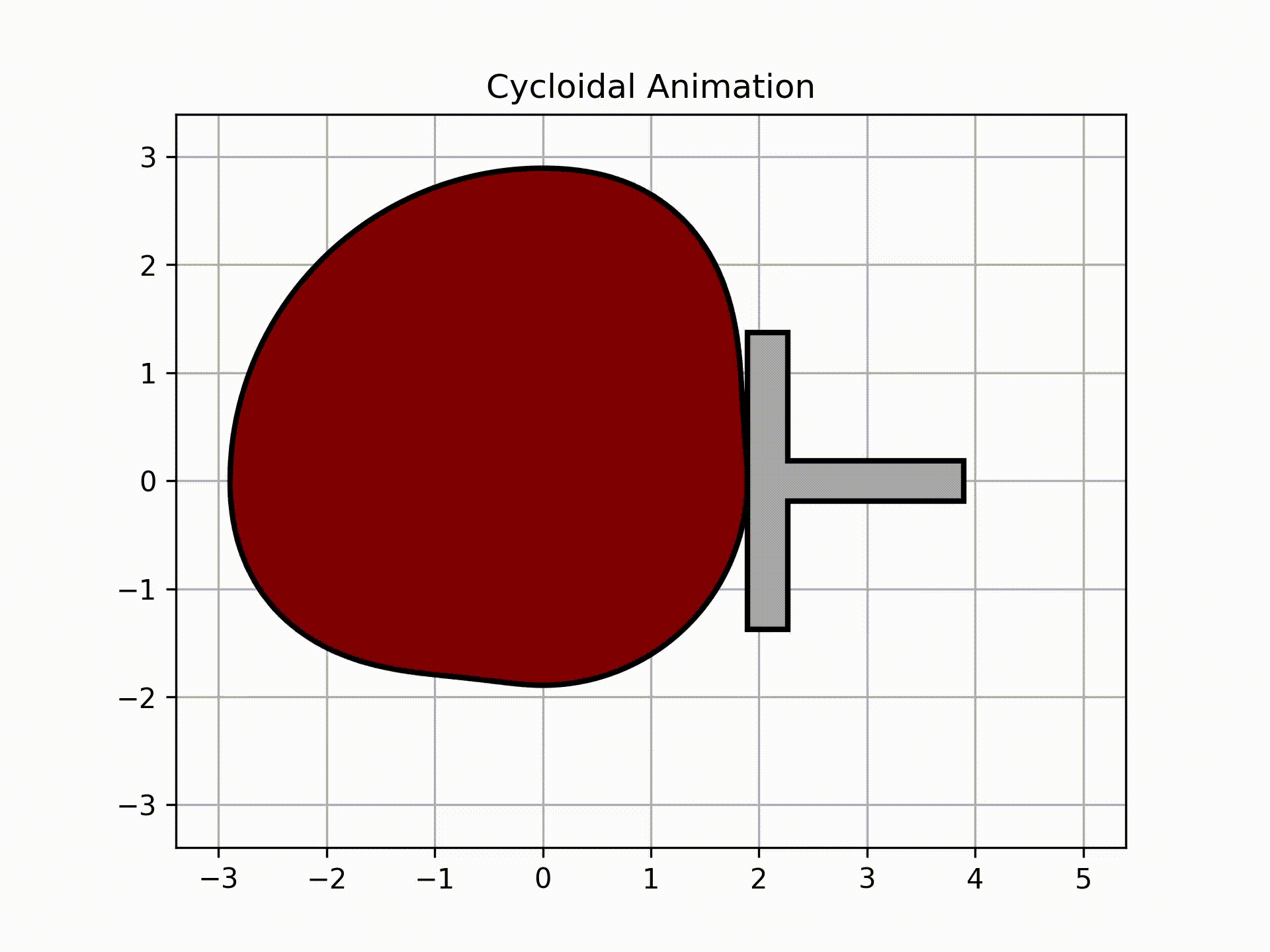
To get the roller animation, call this:
ani, follower = cam.get_animation(kind='cycloidal', base=roller_analysis['Rb'], roller_radius=1/2, length=2, width=3/8,
inc=5)
follower.plot()
Output:
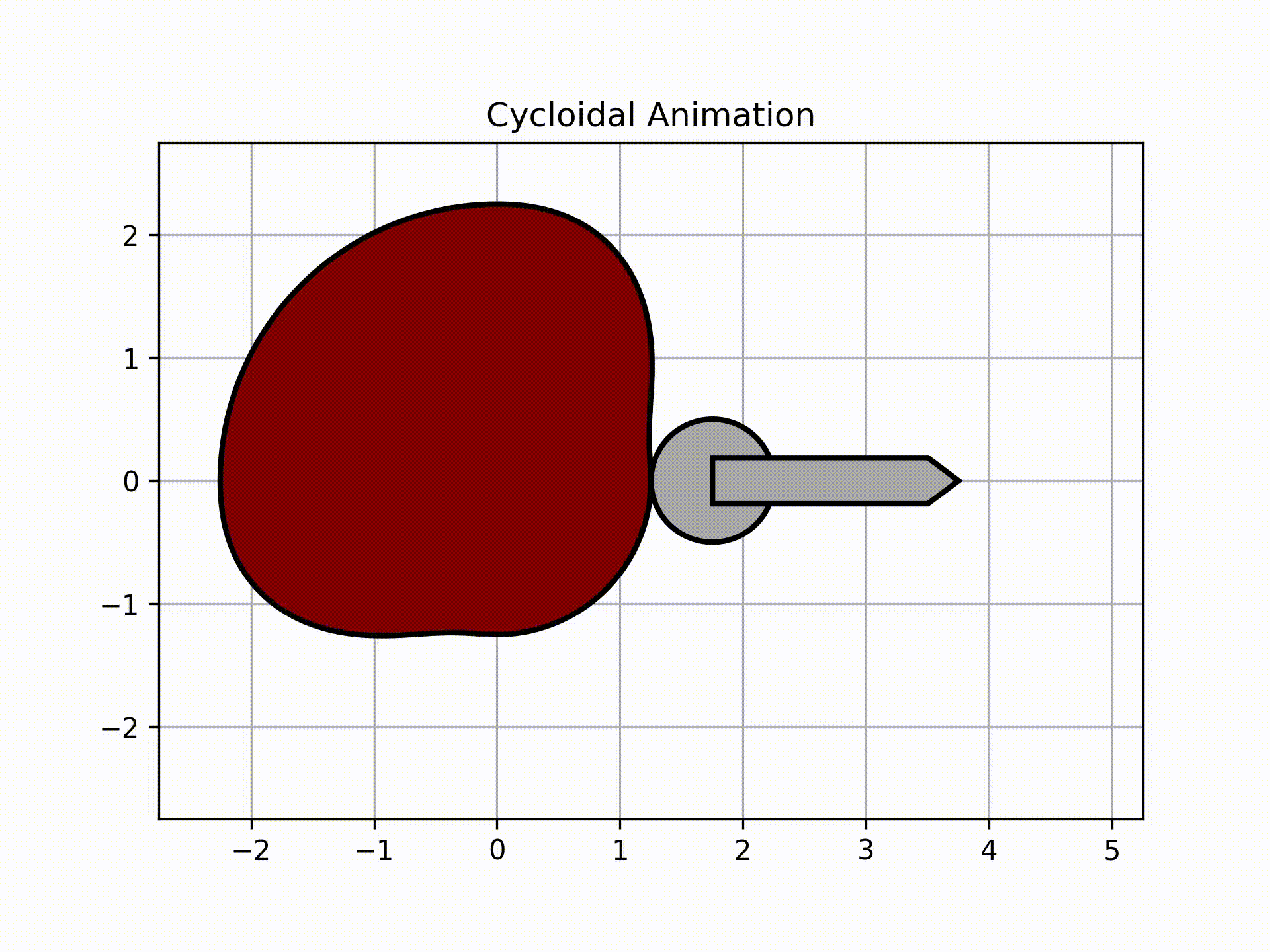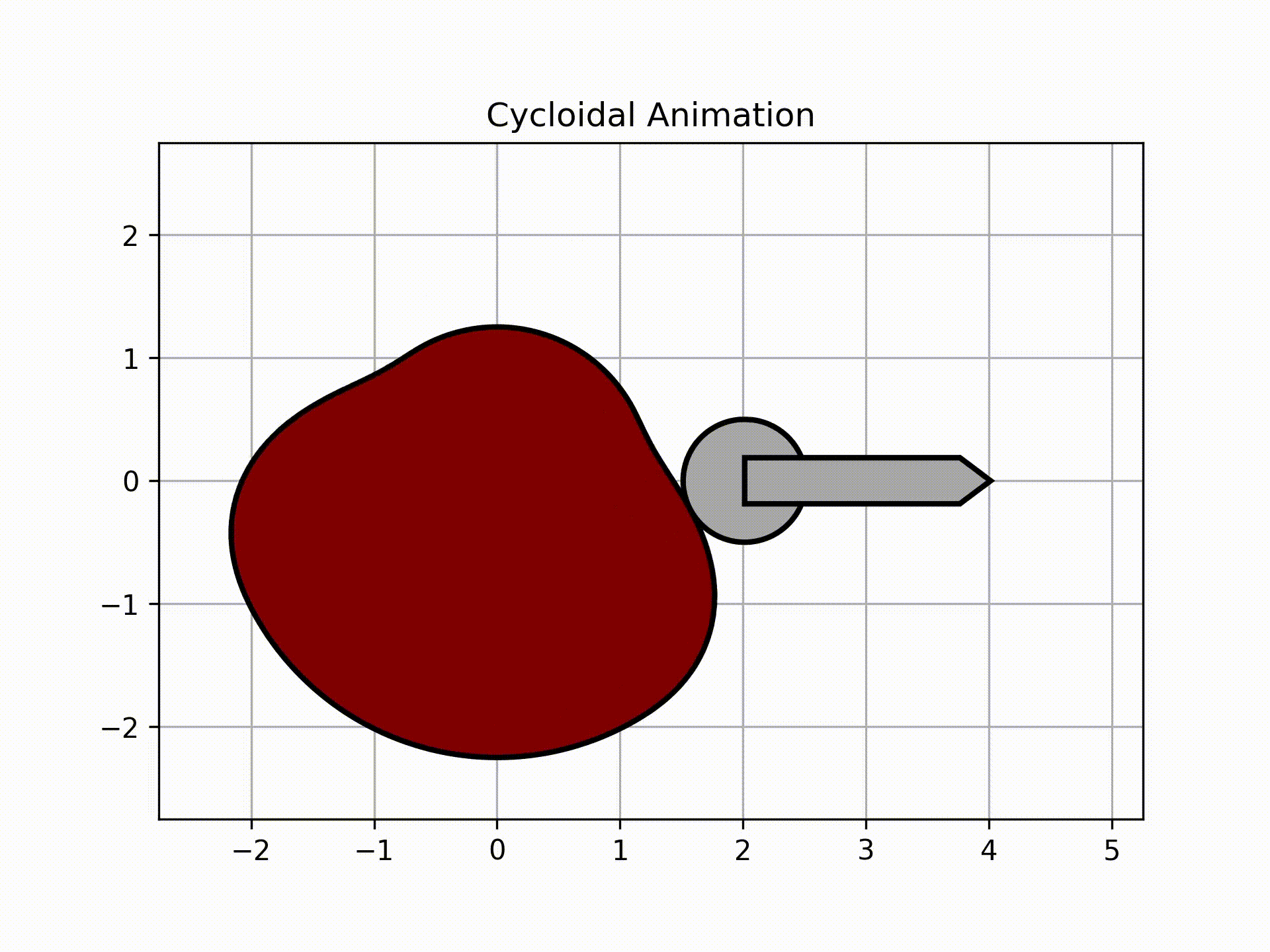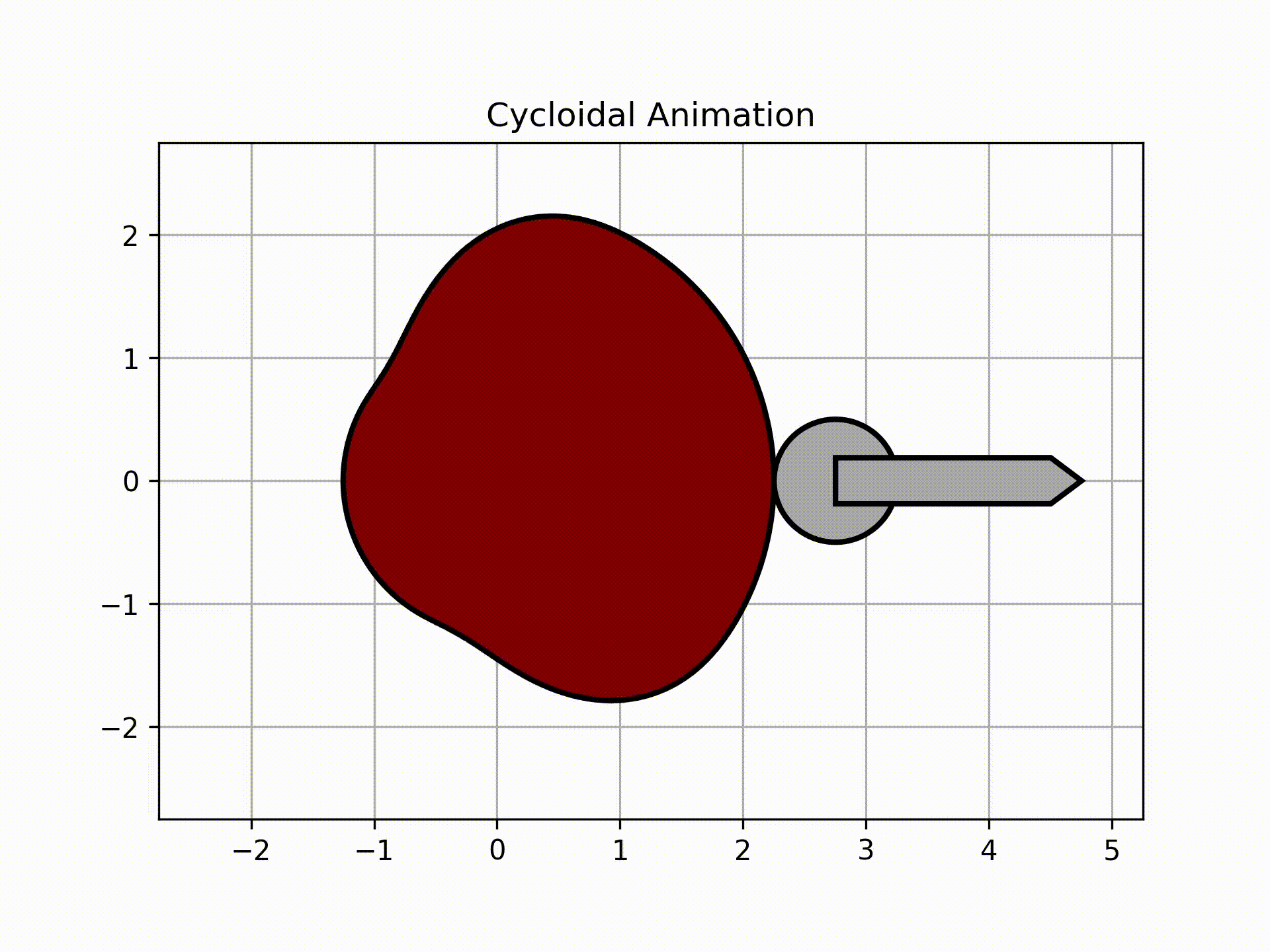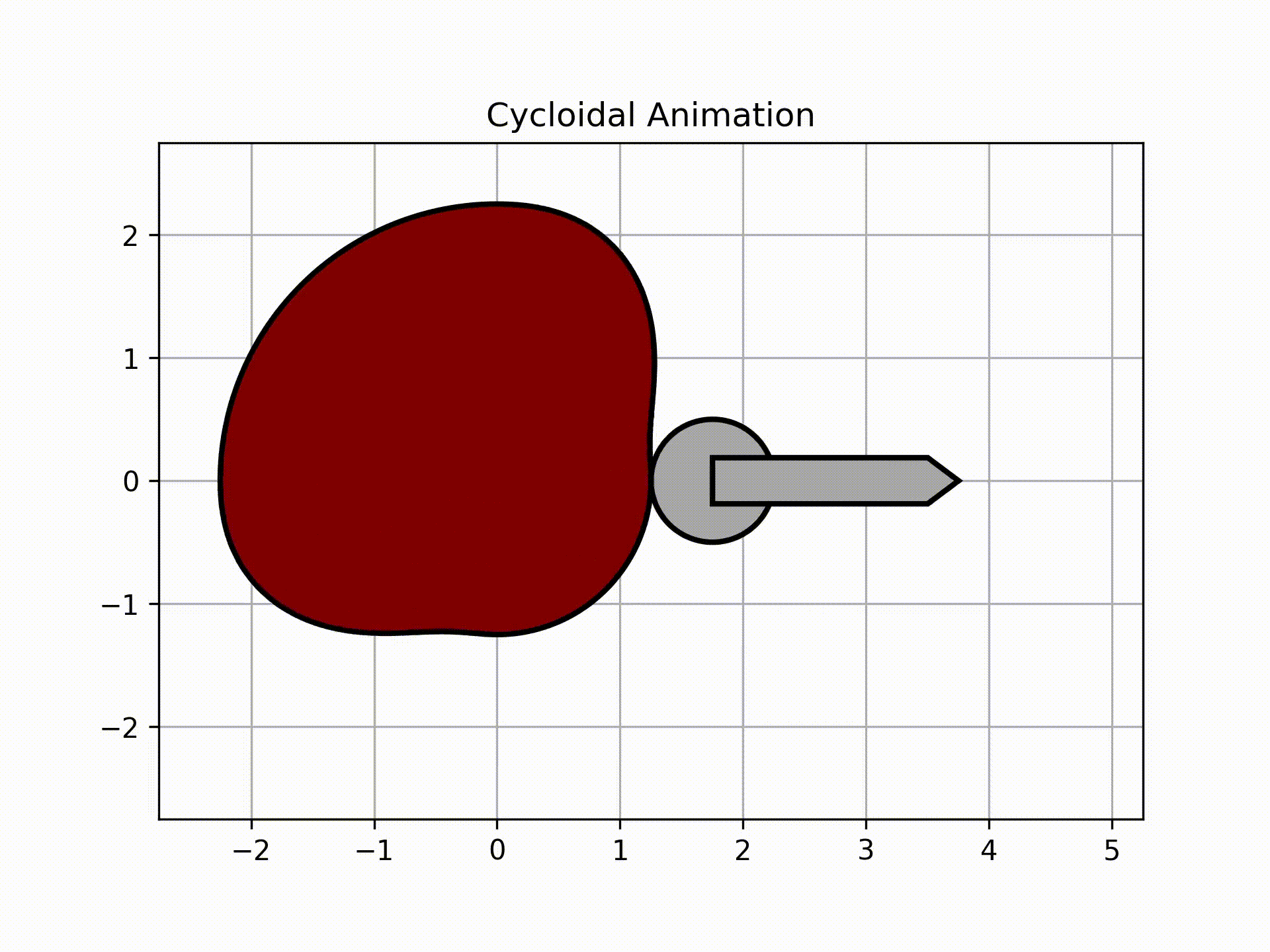
The graph above shows the actual follower displacement due to the circle having to always be tangent to the surface of the cam. Note that as a result of this physical limitation, the follower will have higher magnitudes of velocity and acceleration.
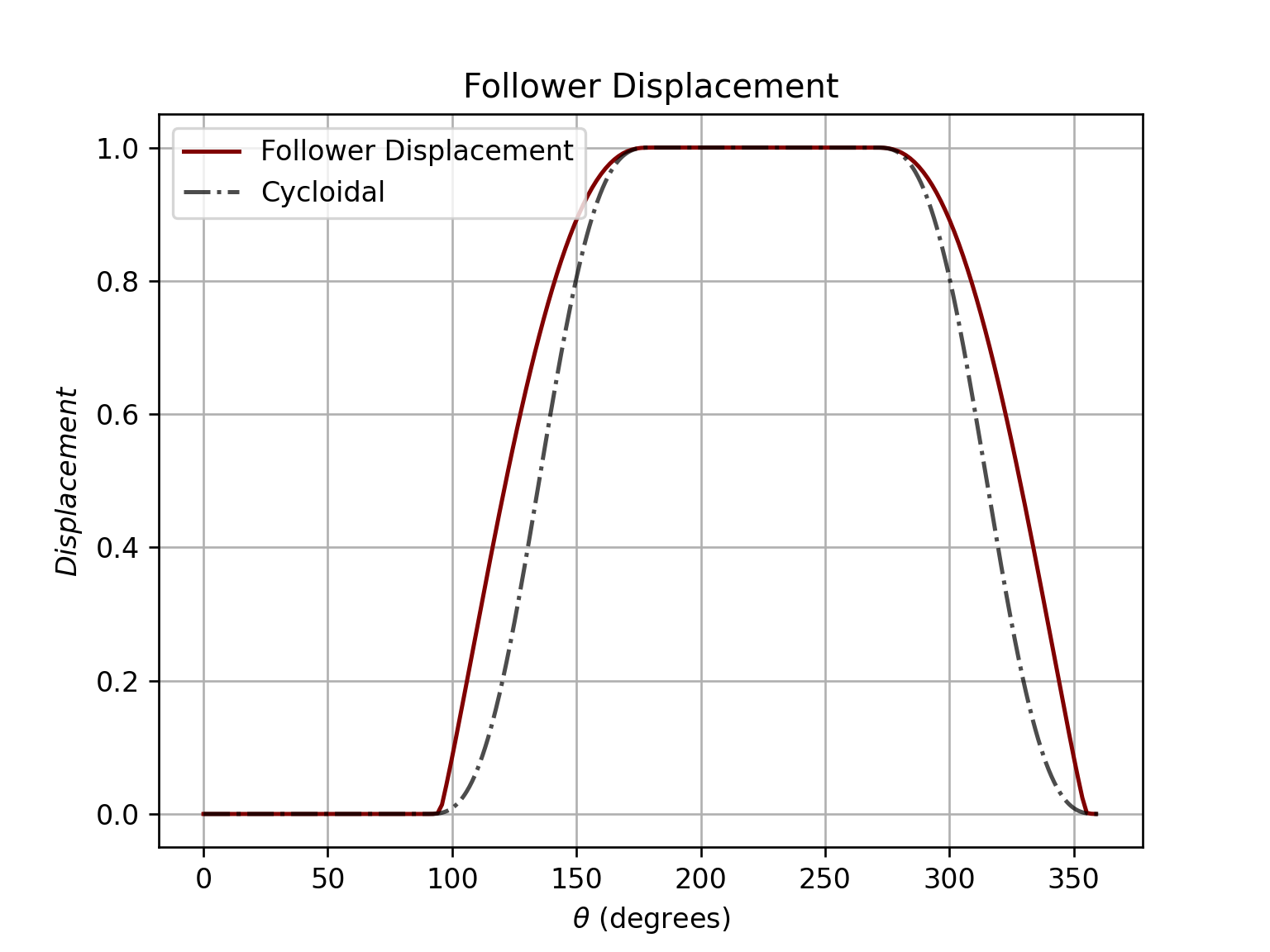
For the flat faced follower,
ani_flat, follower = cam.get_animation(kind='cycloidal', base=flat_analysis['Rb'], face_width=2.75, length=2, width=3/8,
inc=5)
follower.plot()
Output:
Getting Coordinates into SolidWorks
Save the coordinates to a text file.
cam.save_coordinates('cam_coordinates.txt', kind='cycloidal', base=1.3, solidworks=True)
Select Curve Through XYZ Points
The cam profile will always be extended to the front plane due to the manner in which SolidWorks defines the global coordinates. Next, select browse and choose the saved coordinate file.
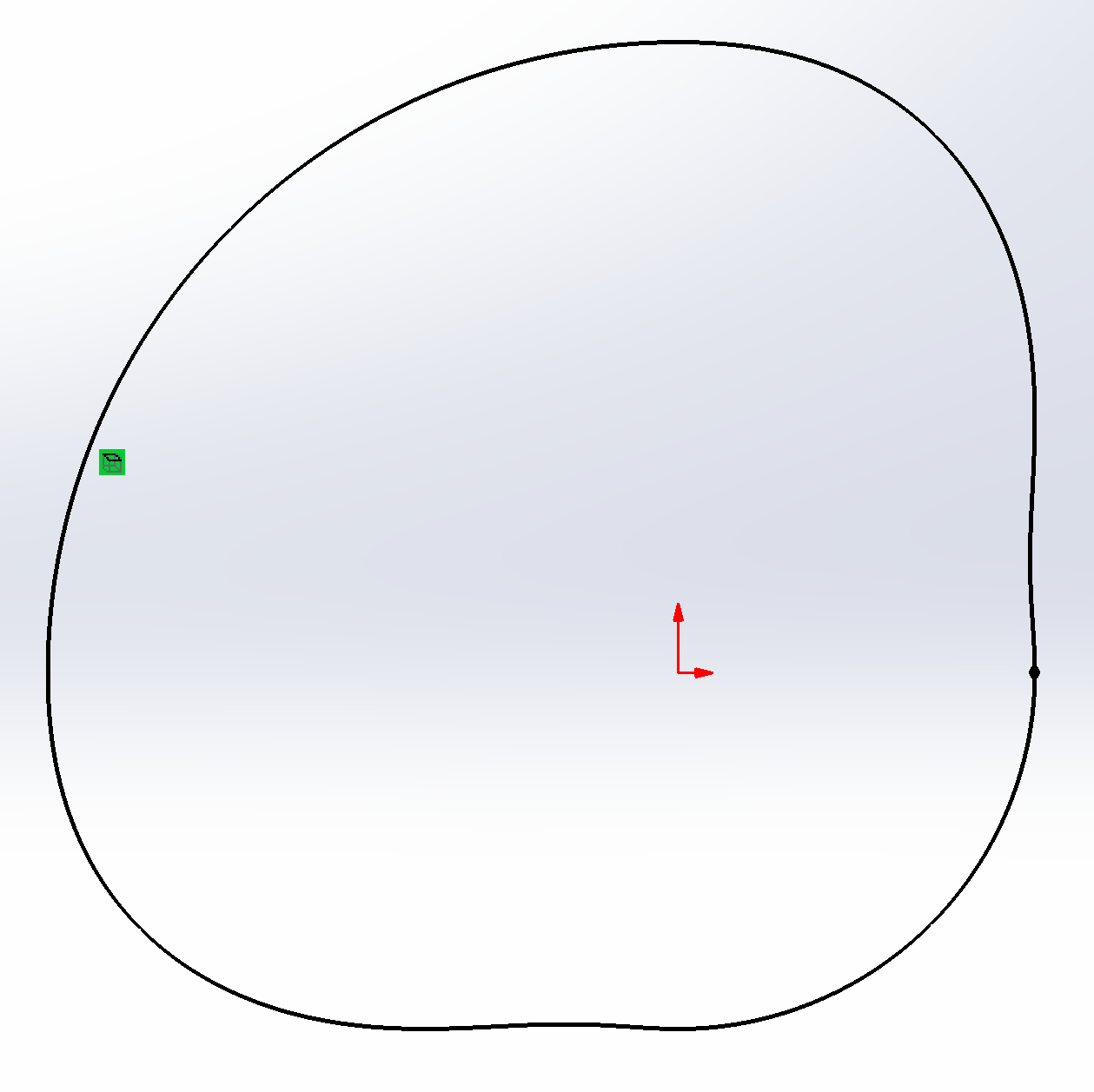
Create a sketch on the front plane. Select the curve and then convert entities. The sketch is now projected to the front plane.
Notice that the sketch is not closed. Add a line to close the sketch, then extrude the sketch.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Hashes for mechanism-0.0.7-py3-none-any.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 249ceed1857877aa48dac857cd081dee6b12860e931e366f36f4f4f4fa9a03a1 |
|
| MD5 | 8823ec0ab09d0e5dd19701f95c9e6bd5 |
|
| BLAKE2b-256 | 1b6c705e22b9623263ab15da9cad293b391791241d4f9005829d05d58b532383 |