Package to perform calculations using the Huzita-Justin axioms for 2-dimensional origami
Project description
Origametry
Python package to perform calculations using the Huzita-Justin axioms for 2-dimensional origami
The Axioms
Discovered by French mathematician Jacques Justin in 1986 and rediscovered by Humiaki Huzita and Koshiro Hatori, these 7 axioms can construct every possible single-fold alignment in the plane.
- Given two distinct points P1 and P2, there is a unique fold that passes through both of them.
- Given two distinct points P1 and P2, there is a unique fold that places P1 onto P2.
- Given two distinct lines L1 and L2, there is a fold that places L1 onto L2.
- Given a point P1 and a line L1, there is a unique fold perpendicular to L1 that passes through point P1.
- Given two points P1 and P2 and a line L1, there is a fold that places P1 onto L1 and passes through P2.
- Given two points P1 and P2 and two lines L1 and L2, there is a fold that places P1 onto L1 and P2 onto L2.
- Given one point P and two lines L1 and L2, there is a fold that places P onto L1 and is perpendicular to L2.
Axiom 3 may have 1 or 2 solutions. Axiom 5 may have 0, 1, or 2 non-trivial solutions. Axiom 6 may have 0, 1, 2, or 3 non-trivial solutions. Axiom 7 may have 0 or 1 non-trivial solutions.
Note that axioms 5, 6 and 7 have infinitely many trivial solutions if any of the points already lie on their required lines.
Installation
pip install origametry
Usage
From only a few starting points, you can generate complex sequences of folds
from origametry import Point, fold, show
point_1 = Point(0, 0)
point_2 = Point(2, 1)
# axiom 2: point onto point
line = fold(point_1, point_2)
# axiom 5: point onto line through another point (2 solutions)
lines = fold(point_1, line, point_2, point_2)
And view your resulting crease pattern (TODO)
show(point_1, point_2, line, lines)
Points
A "point" is a simple container object for 2-dimensional Cartesian coordinates.
point = Point(3, 5)
point.x
# 3
point.y
# 5
Lines
A straight line (or "crease") in the plane can be created in several ways:
- two distinct points
point_1 = Point(3, 5)
point_2 = Point(8, 13)
line = Line(point_1, point_2)
- coefficients of standard-form equation
ax + by + c = 0
line = Line(1, 3, -2)
# `c` defaults to 0
line = Line(1, 3)
- point and gradient
point = Point(2.5, 0)
line = Line(point, .75)
- gradient through origin
# the line y = 0 (horizontal through the origin)
line = Line(0)
# the line y = x
line = Line(1)
# vertical line
line = Line(math.inf)
- as the result of a fold
intersection
A point can also be created at the intersection of two lines. This method returns None is the lines are parallel (i.e. they do not intersect).
point = line_1.intersection(line_2)
Folds
A "fold" is a reflection of points and/or lines across a crease. Origametry exports two functions for working with folds: fold and reflect.
The reflect function simply returns the reflection of a point or line across a given crease:
point_2 = reflect(point_1, crease)
line_2 = reflect(line_1, crease)
The fold function is much more complex. It takes a pairwise series of points and/or lines and tries to find a fold that reflects every element onto its pair. The function returns the crease of that fold or a list of creases, or None if no such fold is possible. This concept is best explained with pictures.
Fold P1 onto P2 (axiom 2):
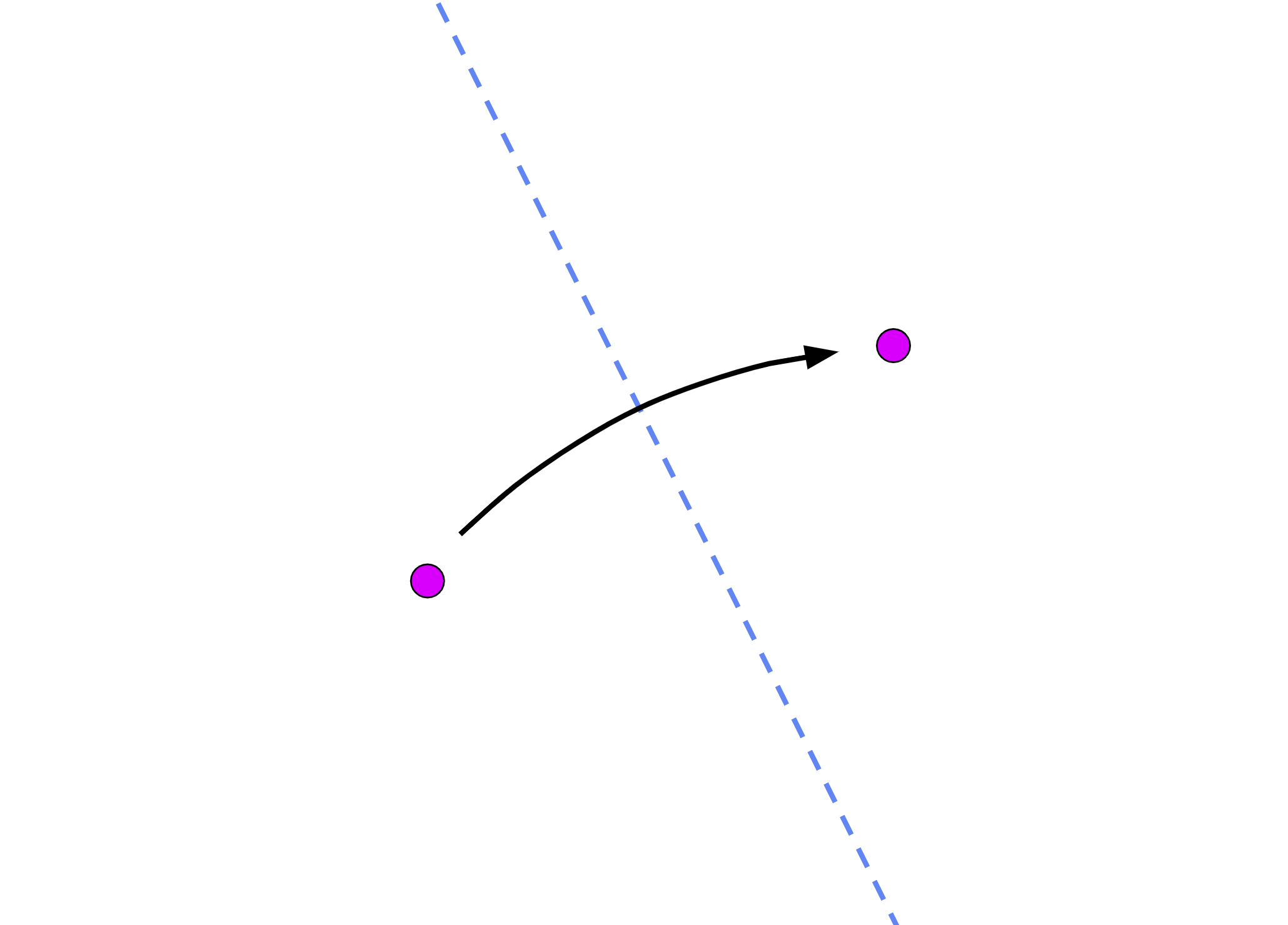
L = fold(P1, P2)
Fold L1 onto L2 (axiom 3):
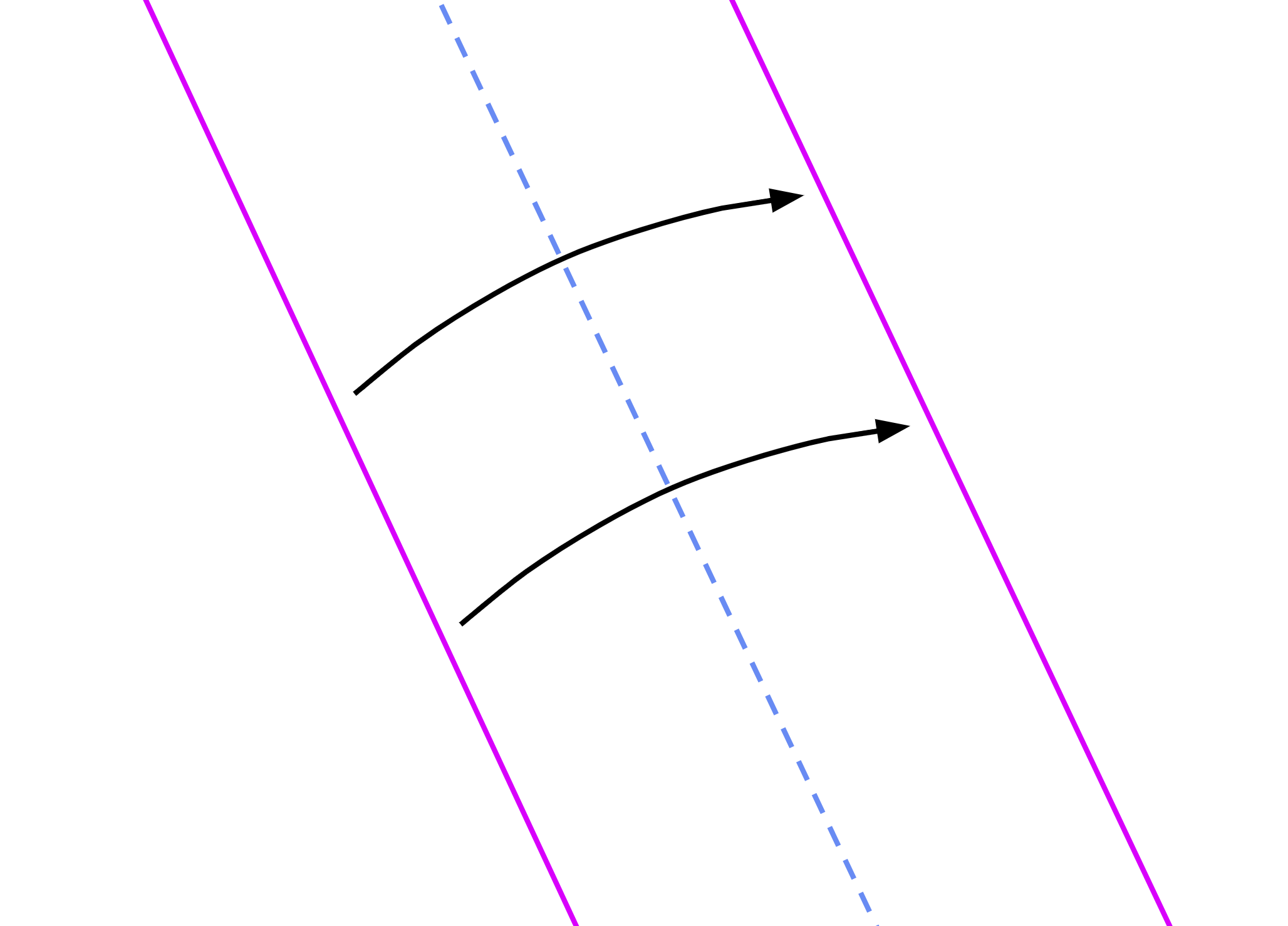
L3 = fold(L1, L2)
If L1 and L2 are not parallel, there are 2 folds that work:
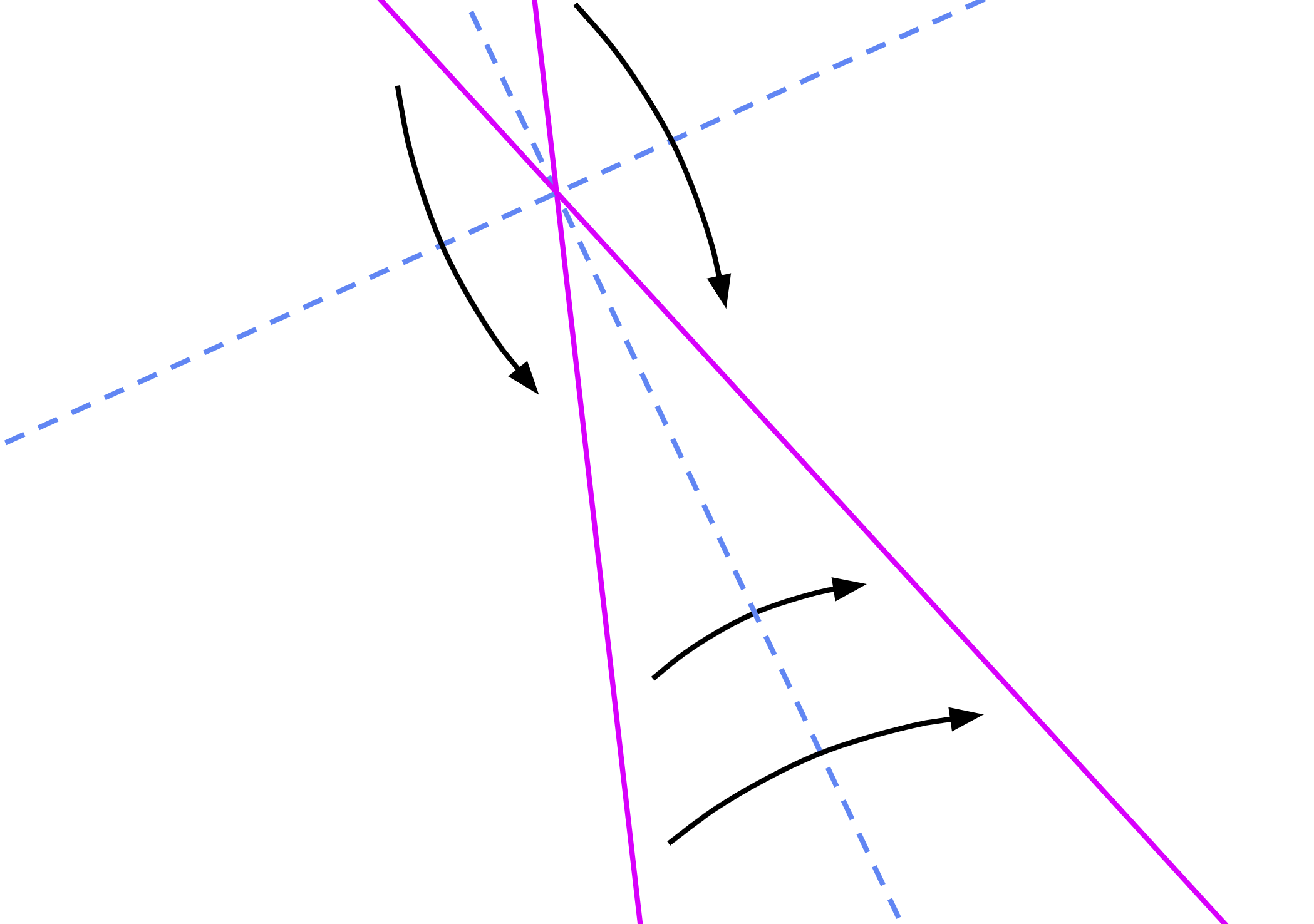
creases = fold(L1, L2)
L3 = creases[0]
L4 = creases[1]
Fold P1 onto L1 AND P2 onto L2 (axiom 6):
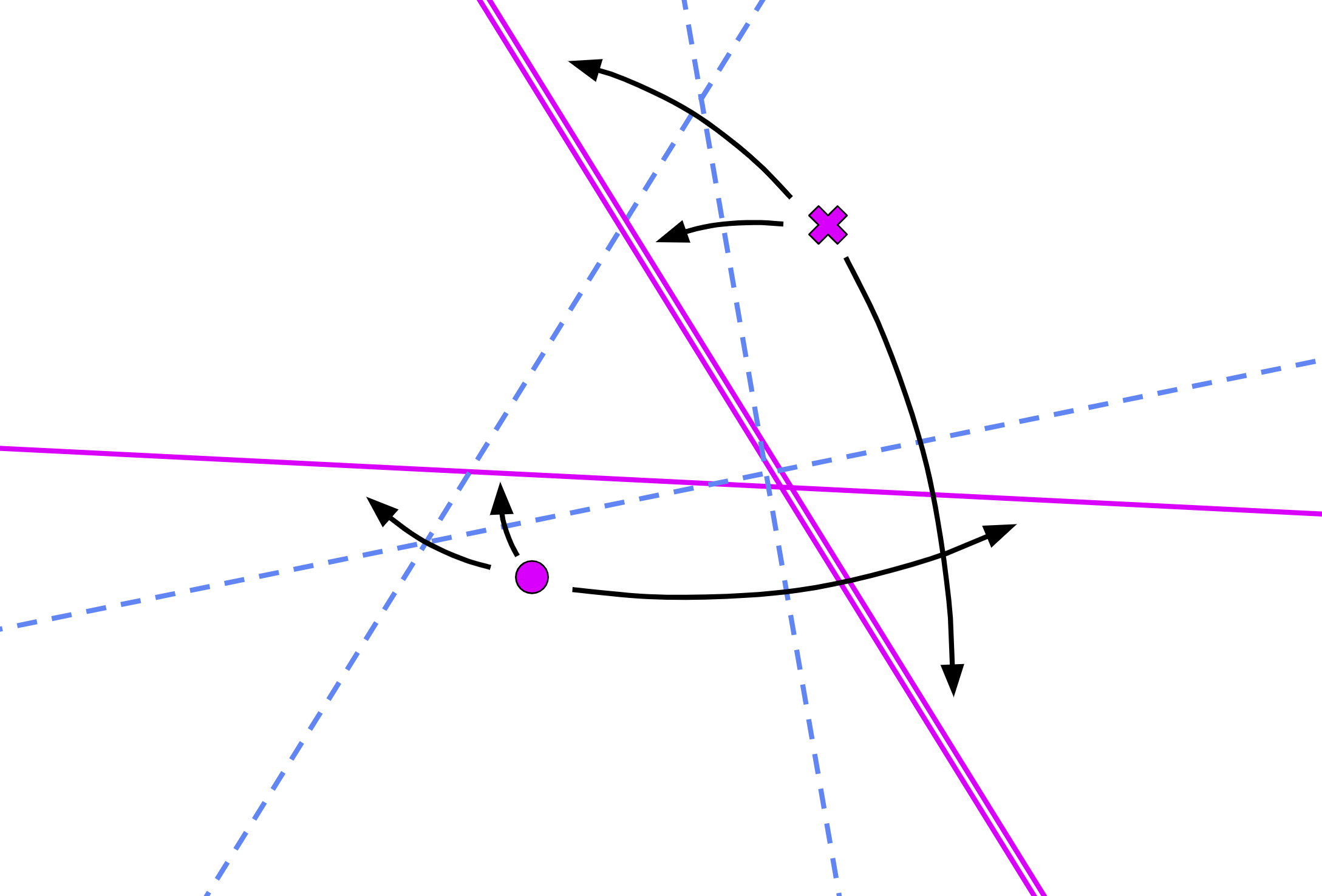
creases = fold(P1, L1, P2, L2)
L3 = creases[0]
L4 = creases[1]
L5 = creases[2]
And here's an example of axiom 6 with no solutions:
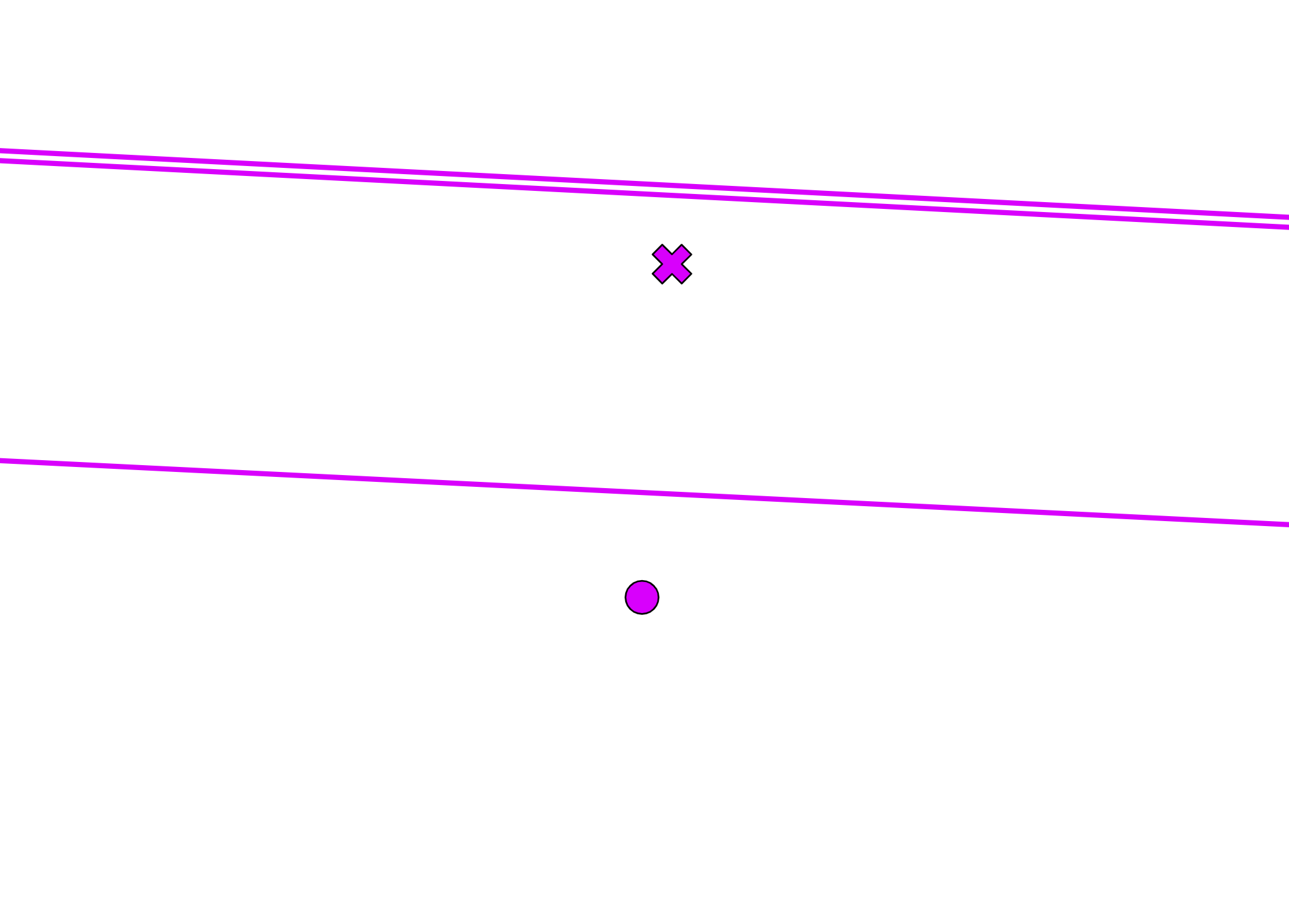
creases = fold(P1, L1, P2, L2)
assert creases == None
Some axioms require that a crease passes through a point. This is equivalent to reflecting that point onto itself.
Thus we can fold through P1 and P2 (axiom 1):
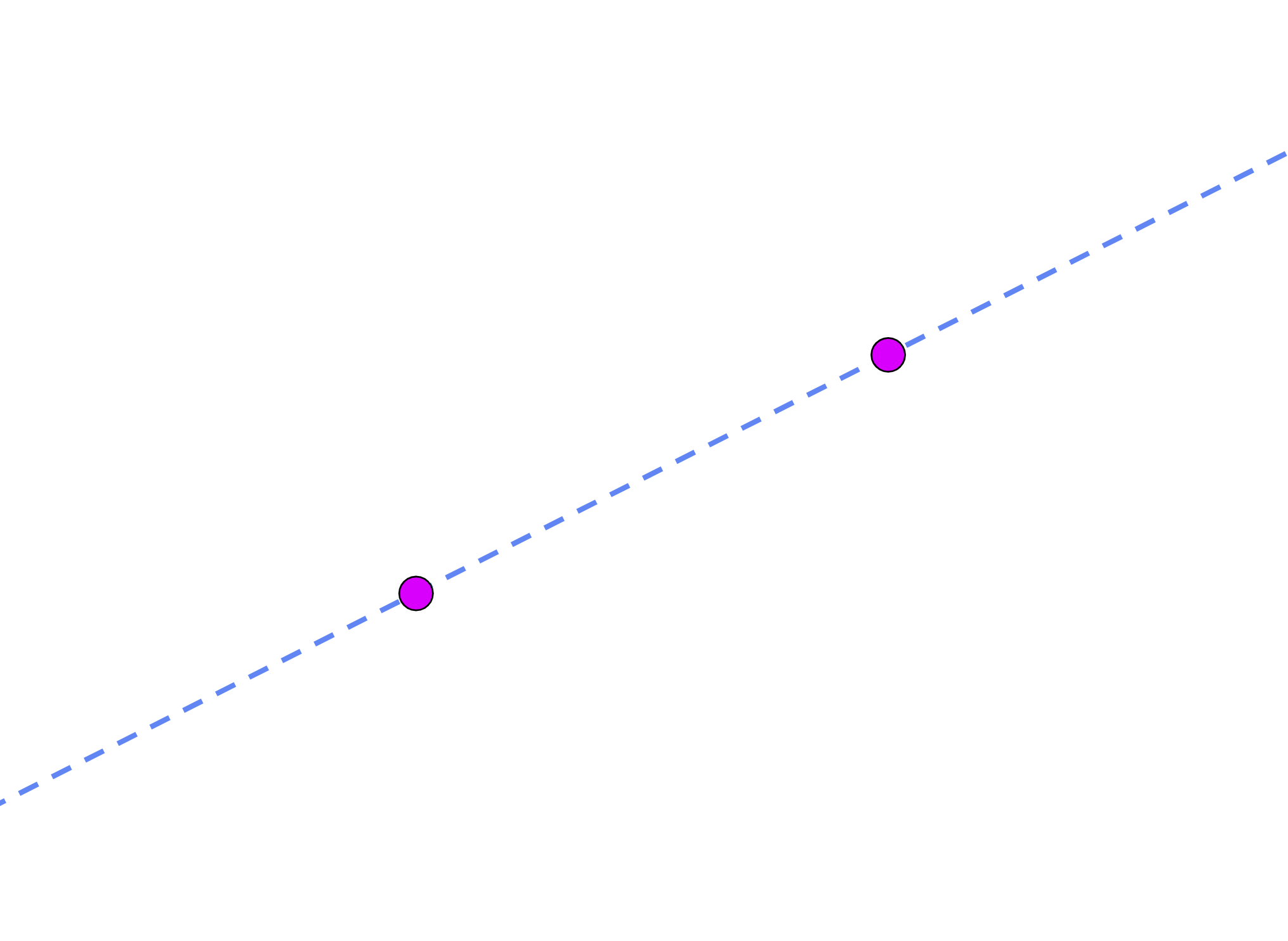
L = fold(P1, P1, P2, P2)
And fold P1 onto L1 through P2 (axiom 5):
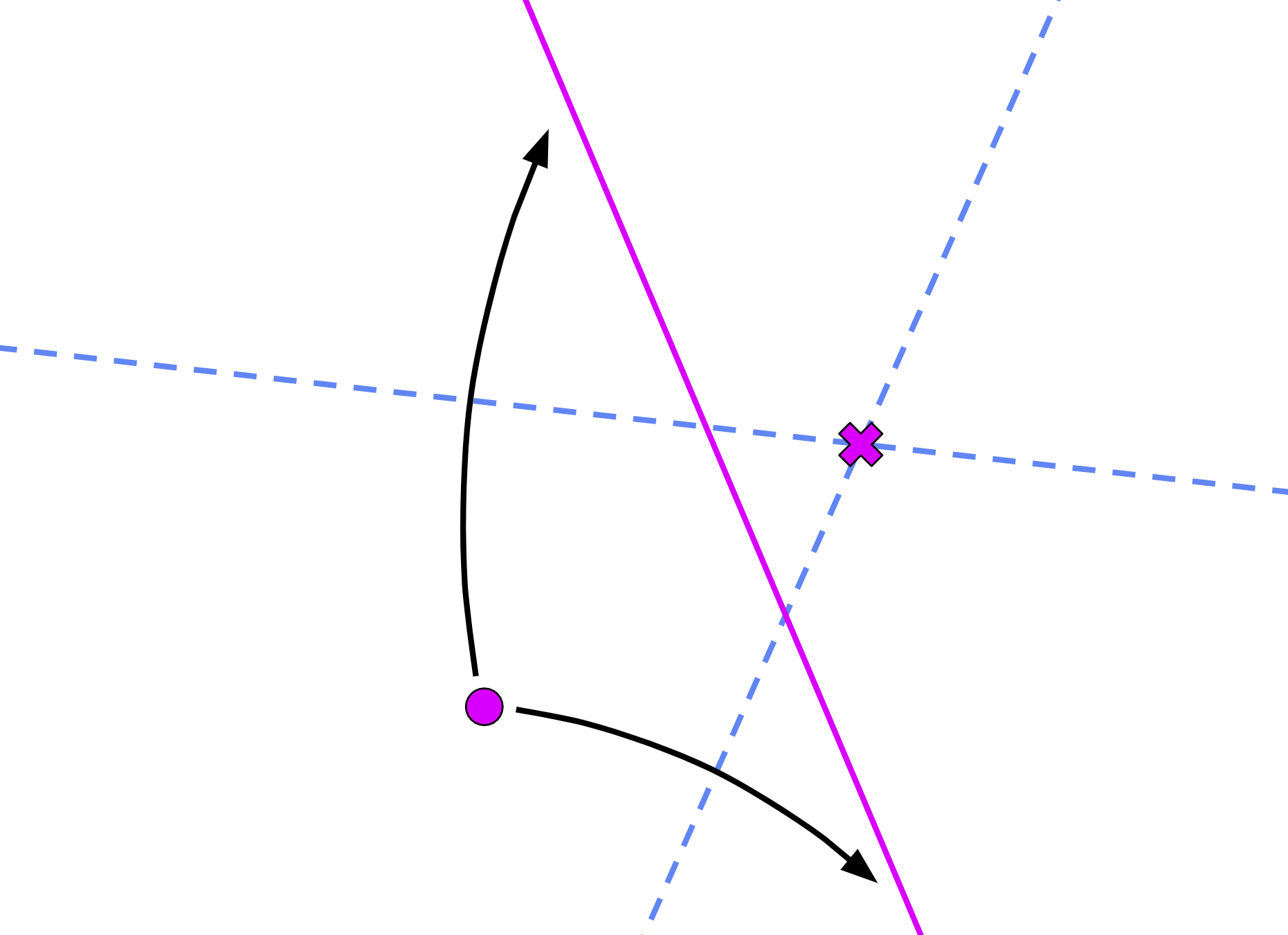
creases = fold(P1, L1, P2, P2)
L2 = creases[0]
L3 = creases[1]
Finally, some axioms require that a crease is perpendicular to a line. This is nearly equivelent to reflecting a line onto itself, with the caveat that a crease going along a line also reflects it onto iself. Since the second case is trivial - the crease is identical to the original line - we choose to always interpret fold(L, L, ...) as being perpendicular to the line L.
Fold through P1 perpendicular to L1 (axiom 4):
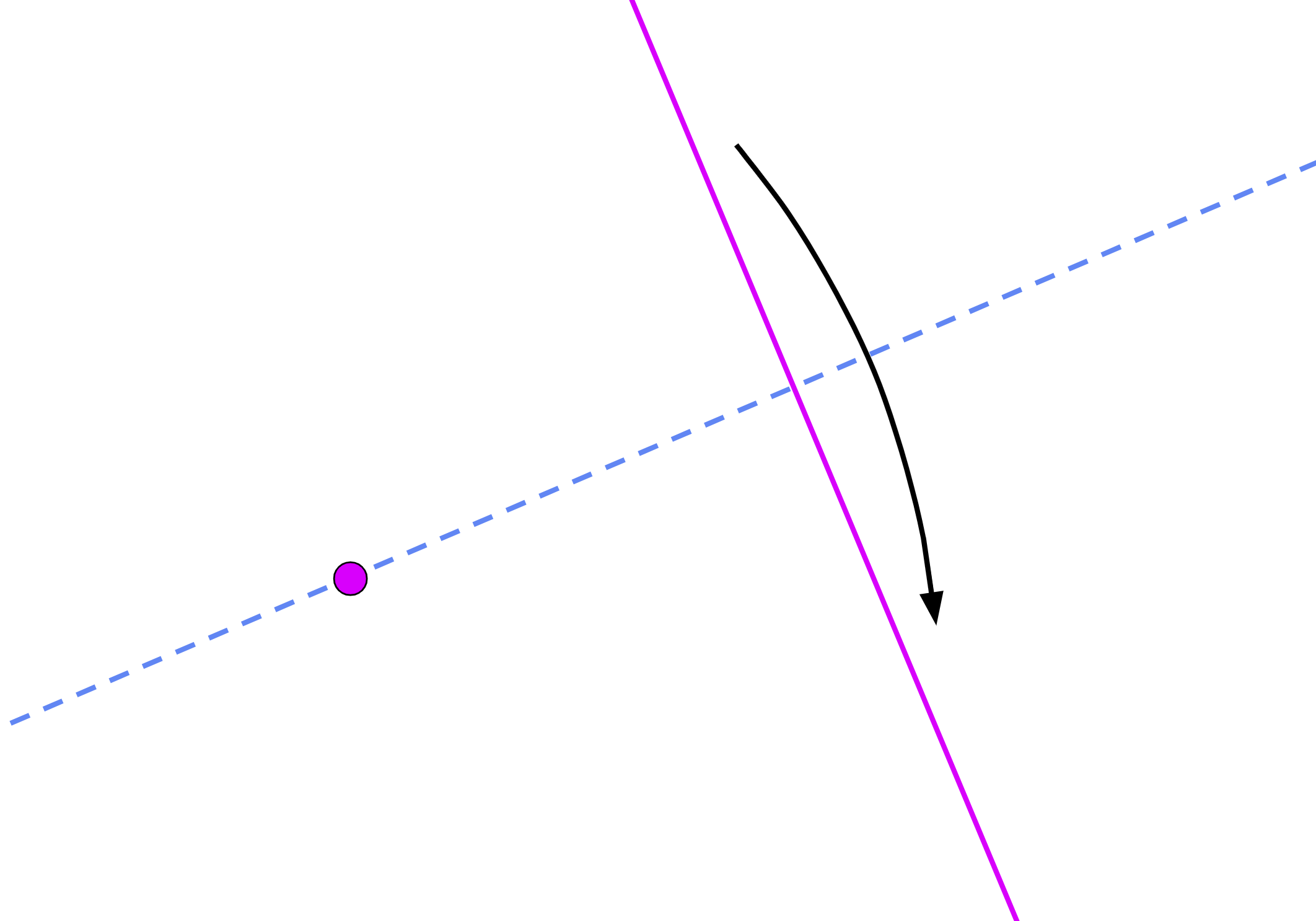
L2 = fold(P1, P1, L1, L1)
Fold P1 onto L1 perpendicular to L2 (axiom 7):
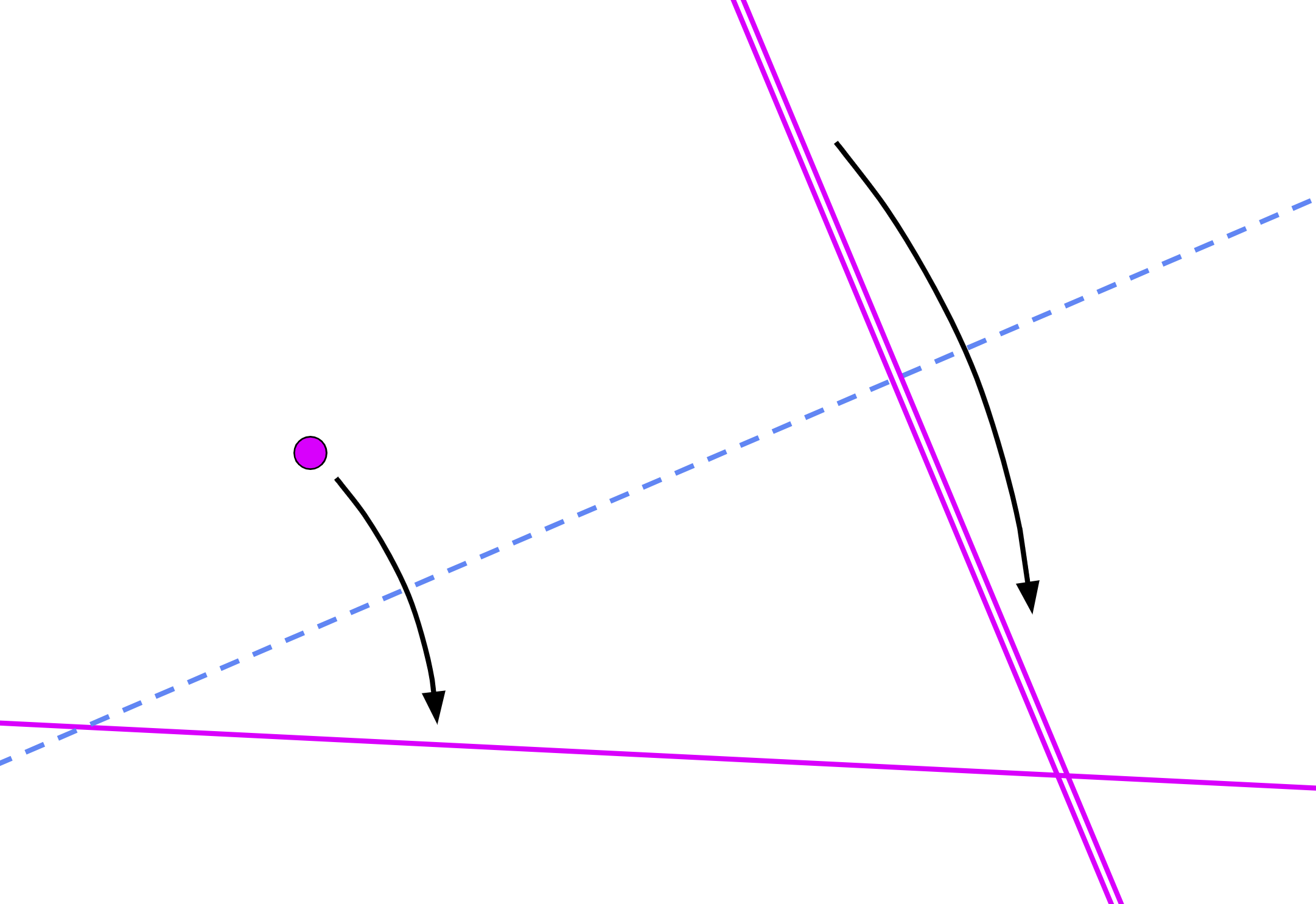
L3 = fold(P1, L1, L2, L2)
An example of axiom 7 with no solutions (L1 and L2 are parallel):

creases = fold(P1, L1, L2, L2)
assert creases == None
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Hashes for origametry-0.0.1-py3-none-any.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | b5e1cd157637c08447b572f91e3901367de2a219fd055084c57528002ba89154 |
|
| MD5 | 19d562b402c5b6dd7af2358048017406 |
|
| BLAKE2b-256 | 00ccde01d78b44a4658256bee9f01309e949981341ea15a391f85af70d9f1668 |











