Python library for organizing objects and dependencies in a graph structure
Project description
Pensieve
Pensieve is a Python library for organizing objects and dependencies in a graph structure.
"One simply siphons the excess thoughts from one's mind, pours them into the basin, and examines them at one's leisure. It becomes easier to spot patterns and links, you understand, when they are in this form."
—Albus Dumbledore (Harry Potter and the Goblet of Fire by J. K. Rowling)

Pensieve for Data
In J. K. Rowling's words: "a witch or wizard can extract their own or another's memories, store them in the Pensieve, and review them later. It also relieves the mind when it becomes cluttered with information. Anyone can examine the memories in the Pensieve, which also allows viewers to fully immerse themselves in the memories".
Dealing with data during data wrangling and model generation in data science is like dealing with memories except that there is a lot more of back and forth and iteration when dealing with data. You constantly update parameters of your models, improve your data wrangling, and make changes to the ways you visualize or store data. As with most processes in data science, each step along the way may take a long time to finish which forces you to avoid rerunning everything from scratch; this approach is very error-prone as some of the processes depend on others. To solve this problem I came up with the idea of a Computation Graph where the nodes represent data objects and the direction of edges indicate the dependency between them.
After using Pensieve for some time myself, I have found it to be beneficial in several ways:
- error reduction, especially for data wrangling and model creation
- data object organization
- easy transfer of data
- coherent data processing and data pipelines
- data and model reproducibility
- parallel processing
- performance and cost analysis in terms of computation time and memory usage
- graphical visualization of data and processes
- most important of all: relieving the mind
Using pensieve is similar to using a dictionary:
from pensieve import Pensieve
from math import pi
# initiate a pensieve
pensieve = Pensieve()
# store a "memory" (with 1 as its content)
pensieve['radius'] = 5
# create a new memory made up of a precursor memory
# it is as easy as passing a defined function or a lambda to pensieve
pensieve['circumference'] = lambda radius: 2 * pi * radius
print(pensieve['circumference'])
outputs:
31.41592653589793
Changing the radius, in this example, will affect the circumference but it is only calculated when needed:
pensieve['radius'] = 6
print(pensieve['circumference'])
outputs
37.69911184307752
Installation
pip install pensieve
Usage
Pensieve stores memories and functions that define the relationship between memories.
Concepts
Memory
A Pensieve is a computation graph where the nodes hold values and edges
show dependency between nodes. Each node is called a Memory.
Every memory has two important attributes:
key: the name of the memory which should be identicalcontent: the object the memory holds
Some memories have two other attributes:
precursors: other memories a memory depends onfunction: a function that defines the relationship between a memory and its precursors
There are two types of memories:
- independent memories (without precursors)
- dependent memories (with precursors)
Storing a Memory
As explained above, you can work with pensieve similar to how you use a
dictionary. Adding a new item, i.e., a memory and its content, to pensieve is
called storing. In fact the Pensieve class has a store method which
can be used for storing new memories. However, we only use it for advanced
functionality. We do not use it as frequently because a new simpler notation
introduced since version 2 makes working pensieve much more coherent.
We will explain the store method and its notation in the Advanced Usage section.
Retrieving a Memory
Retrieving the content of a memory is like getting an item from a dictionary.
print(pensieve['circumference'])
Independent Memories
An independent memory is like a root node in pensieve. It holds an object and it does not depend on any other memory.
from pensieve import Pensieve
pensieve = Pensieve()
pensieve['text'] = 'Hello World!'
pensieve['number'] = 1
pensieve['list_of_numbers'] = [1, 3, 2]
In the above example, text, number, and list are the names of three
independent memories and their contents are
the string 'Hello World',
the integer 1,
and a list consisting of three integers.
Dependent Memories and Precursors
A dependent memory is created from running a function on other dependent or independent memories as the function's arguments. We call those memories, precursors; i.e., if a memory depends on another memory, the former is a dependent memory and the latter is its precursor.
The easiest way to define a dependent memory is by passing a function to pensieve whose arguments match the names of precursors.
def print_and_return_first_word(text):
words = text.split()
print(words[0])
return words[0]
pensieve['first_word'] = print_and_return_first_word
In the above example, the print_and_return_first_word function accepts one argument:
text which is the name of the precursor.
You can also use a lambda, when possible, to define a dependent memory.
pensieve['sorted_list'] = lambda list_of_numbers: sorted(list_of_numbers)
Successors
Memories that depend on a memory are its successors. If a precursor is like a parent, a successor is like a child.
In the above example, sorted_list is a successor of list_of_numbers.
Staleness
If one or more precursors of a memory change, the memory and all its successors becomes stale. A stale memory is only refreshed when needed and if after calculation, it is found out that the content has not changed, the successors go back to being up-to-date, but if the content has in fact changed, the stay stale and will be updated when needed.
Note: if a memory is stale, retrieving its content will update it.
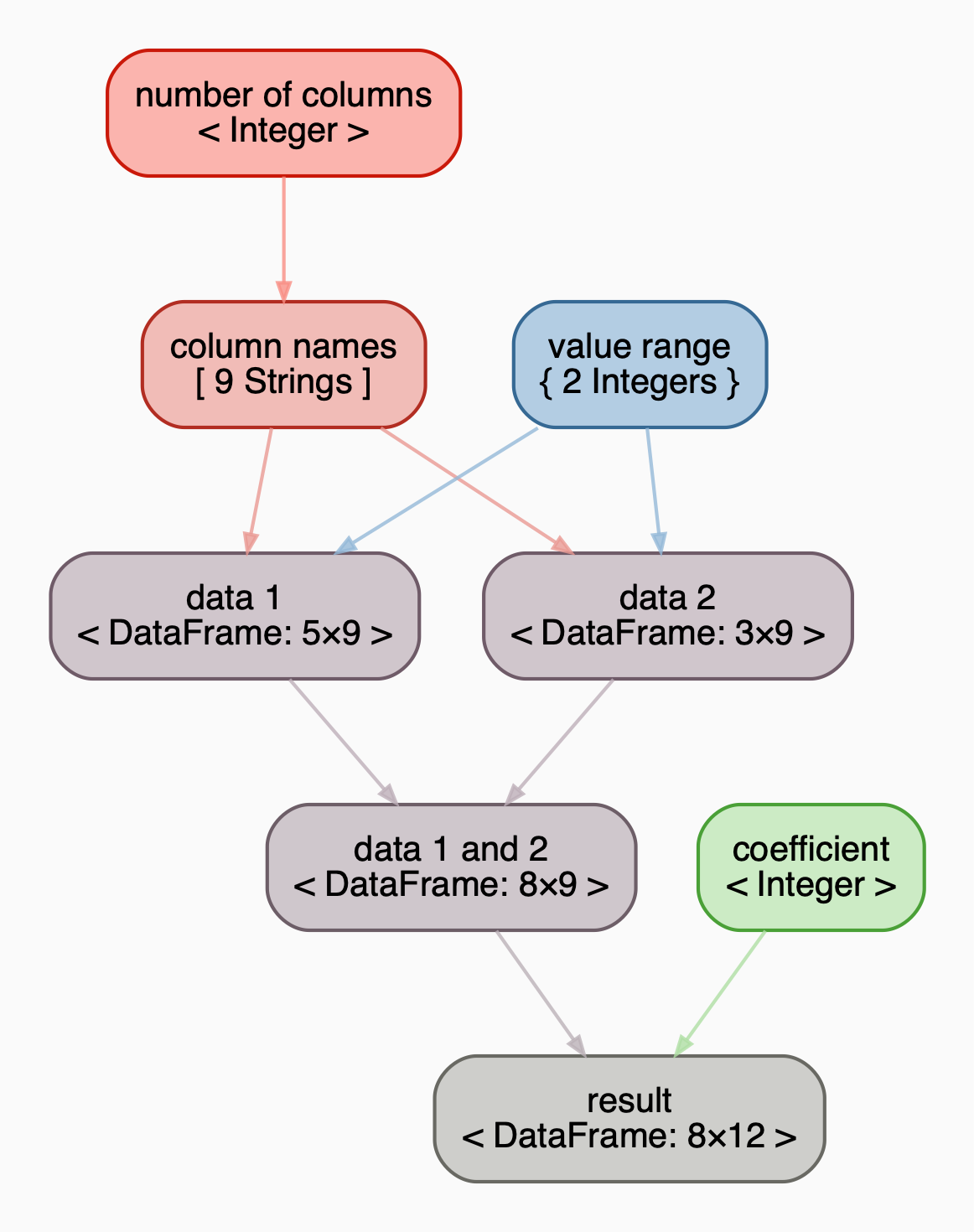
Visualization
from pensieve import Pensieve
from pandas import DataFrame, concat
from numpy.random import randint, seed
# set seed for the randint function
seed(17)
# set up a pensieve with a top-bottom (tb) representation
# the top-bottom graph_direction is purely aesthetic
# you can also use lr for left to right or rl for right to left or bottom-top
pensieve = Pensieve(graph_direction='tb')
# choose the number of columns for two dataframes
pensieve['number_of_columns'] = 9
# create generic names for the columns, in this case x_1, x_2, ...
pensieve['column_names'] = lambda number_of_columns: [
f'x_{i + 1}' for i in range(number_of_columns)
]
# choose the range of random values, and store them as a dictionary
pensieve['value_range'] = {'low': 1, 'high': 5}
# define a function that creates a dataframe with the above parameters
def create_dataframe(column_names, value_range, number_of_rows):
return DataFrame({
column: randint(
low=value_range['low'],
high=value_range['high'],
size=number_of_rows
)
for column in column_names
})
# create the first dataframe
pensieve['data_1'] = lambda column_names, value_range: create_dataframe(
column_names=column_names, value_range=value_range, number_of_rows=5
)
# create the second dataframe
pensieve['data_2'] = lambda column_names, value_range: create_dataframe(
column_names=column_names, value_range=value_range, number_of_rows=3
)
# concatenate the two dataframes
pensieve['data_1_and_2'] = lambda data_1, data_2: concat(
objs=[data_1, data_2],
sort=False
)
# choose a coefficient for a future multiplication
pensieve['coefficient'] = 5
# define a function that sums all the values in each row and
# multiplies the result by the coefficient
def sum_and_multiply(data_1_and_2, coefficient):
data = data_1_and_2.copy()
data['summation'] = data.apply(sum, axis=1)
data['coefficient'] = coefficient
data['y'] = data['summation'] * data['coefficient']
return data
# get the result of the sum_and_multiply function
pensieve['result'] = sum_and_multiply
# display the pensieve
display(pensieve)
# or simply pensieve at the end of a jupyter notebook cell
Advanced Usage
Parallel Processing
from pensieve import Pensieve
from time import sleep
from datetime import datetime
# as in other libraries, num_threads=-1 means
# using as many threads as available
start_time = datetime.now()
pensieve = Pensieve(num_threads=-1, evaluate=False)
pensieve['x'] = 1
pensieve['y'] = 10
pensieve['z'] = 2
pensieve['w'] = 20
def add_with_delay(x, y):
print(f'adding {x} and {y}, slowly, at {datetime.now()}')
sleep(1)
return x + y
pensieve['x_plus_y'] = add_with_delay
pensieve['z_plus_w'] = lambda z, w: add_with_delay(x=z, y=w)
# we had to use a lambda for this one because the arguments
# of the add_with_delay function are different
pensieve['all_the_four'] = lambda x_plus_y, z_plus_w: add_with_delay(x=x_plus_y, y=z_plus_w)
elapsed = datetime.now() - start_time
print('Nothing has been calculated yet. Elapsed time:', elapsed)
print('Getting all_the_four forces the calculation of everything')
start_time = datetime.now()
print('Result of adding the four numbers:', pensieve['all_the_four'])
elapsed = datetime.now() - start_time
print('Elapsed time:', elapsed)
The above code produces the following output:
Nothing has been calculated yet. Elapsed time: 0:00:00.000716
Getting all_the_four forces the calculation of everything
adding 2 and 20, slowly, at 2019-12-15 21:33:55.063888
adding 1 and 10, slowly, at 2019-12-15 21:33:55.064526
adding 11 and 22, slowly, at 2019-12-15 21:33:56.188258
Result of adding the four numbers: 33
Elapsed time: 0:00:02.341677
Two of the calculations were executed in parallel: x + y and z + w.
With an overhead of 0.34 seconds, the three calculations took 2.34 seconds.
Let's see what happens if we do it the ordinary way:
start_time = datetime.now()
x = 1
y = 10
z = 2
w = 20
x_plus_y = add_with_delay(x, y)
z_plus_w = add_with_delay(z, w)
all_the_four = add_with_delay(x_plus_y, z_plus_w)
print('Result of adding the four numbers:', all_the_four)
elapsed = datetime.now() - start_time
print('Elapsed time:', elapsed)
This time the following output is produced:
adding 1 and 10, slowly, at 2019-12-15 21:38:11.618910
adding 2 and 20, slowly, at 2019-12-15 21:38:12.620105
adding 11 and 22, slowly, at 2019-12-15 21:38:13.625195
Result of adding the four numbers: 33
Elapsed time: 0:00:03.011291
With an overhead of 0.01 seconds, the three calculations
ran one after the other and took 3.01 seconds.
The store Method
TBD
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Hashes for pensieve-2021.8.20-py3-none-any.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 72f0e0eeb5698b4a8dc907640961478f05acb222e481b35ab1b6fefee120ab9d |
|
| MD5 | bde7979535d190dbd2ff09c131054270 |
|
| BLAKE2b-256 | 0cc0bc08eaf2934f8f1e4d26a4e9991fbc6d4b4b19166842b0c2a9799f01c5e5 |











