A Pytorch dataset for Acoustic Wave Propagation
Project description

PyAWD: a Python acoustic wave propagation dataset using PyTorch and Devito
A package for generating Pytorch datasets containing simulations of the acoustic wave propagation in custom velocity fields.
Acoustic Wave Equation
The equation of propagation of an acoustic wave is given by $\frac{d^2u}{dt^2} = c \nabla^2 u + f$, where
- $u(x, y, t)$ is the displacement field and can be either a scalar or a vector field
- $c(x, y, t)$ is the wave propagation speed
- $\nabla^2$ is the laplacian operator
- $f(x, y, t)$ is an external force applied on the system, for which the value can vary through time PyAWD uses the Devito Python Library to solve the acoustic wave PDE from various random initial conditions.
Installation
The package (along with the dependencies) is accessible via PyPI:
pip install pyawd
Documentation
The API documentation is available here.
Basic help is provided for each class and function and is accessible via the Python help() function.
We provide a bunch of Notebooks to start using the tool. They are presented in the examples directory. Those are readable online:
ScalarAcousticWavePropagation.ipynb: an introduction to PDE solving and simulation using Devito applied on the scalar acoustic wave propagationVectorAcousticWavePropagation.ipynb: an introduction to PDE solving and simulation using Devito applied on the vector acoustic wave propagationVectorAcousticWaveDataset.ipynb: an introduction to the VectorAcousticWaveDataset possibilitiesMarmousi.ipynb: a visualisation of the Marmousi velocity field used in the simulationsInterrogators.ipynb: an introduction to the PyAWD Interrogators usageGenerateVectorAcousticWaveDataset.ipynb: how to generate dataset usingpyawdSpatioTemporalVaryingWavePropagationSpeedField.ipynb: how to create a spatio-temporal varying propagation field
Getting started
Basic imports:
from pyawd import *
Let us generate a Dataset made of 10 simulations. Each simulation is run in a $250\times 250$ matrix. We store the field state every $2$ seconds and we run the simulation for $10$ seconds:
dataset = VectorAcousticWaveDataset2D(2, nx=128, dt=2, t=10, velocity_model="Marmousi")
dataset.max_velocities[0] = 500
Then we plot the first simulation. The 🟀 character shows the interrogator position:
dataset.plot_item(0)
Which outputs the following figure:

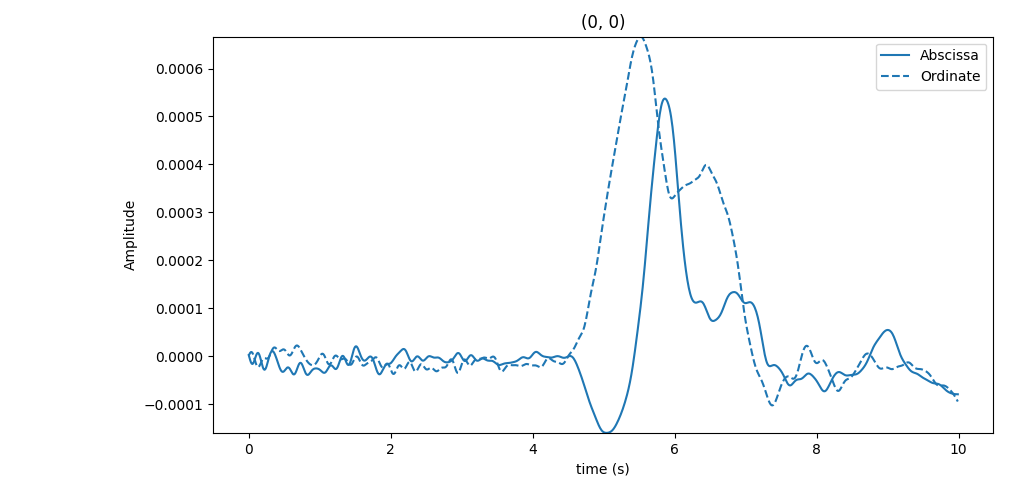
By default, the point (0, 0) contains an interrogator. This means that the continuous measurement on this position (at least with a $\Delta t=ddt$) can be plotted by:
dataset.plot_interrogators_response(0)
More advanced usage
Using the VectorAcousticWaveDataset3D class allows producing simulations in 3D:
dataset_3d = VectorAcousticWaveDataset3D(1, nx=32, t=10, interrogators=[(0, 10, 15), (0, -10, 15)], velocity_model=300.)
For visualisation, the method
dataset_3d.generate_video(0, "VAWD3D", 300)
generates the following video:
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file pyawd-0.3.75.tar.gz.
File metadata
- Download URL: pyawd-0.3.75.tar.gz
- Upload date:
- Size: 226.7 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | be81df329d0c0e79598392e2cef0a0366b7fd2b30d62ab1f4a3bce8f01ba887e |
|
| MD5 | 54bccc75deaa1972cab2146baf118bac |
|
| BLAKE2b-256 | 56bd5782b0f4b98c162832cb0b5d6b4849ae0ef9f1fd7686b256c4e215916922 |
File details
Details for the file pyawd-0.3.75-py3-none-any.whl.
File metadata
- Download URL: pyawd-0.3.75-py3-none-any.whl
- Upload date:
- Size: 266.2 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | b65b6002be7dac5e8b8dfc04f14b64a54aeb09a48df137ad8b87d331e08d968f |
|
| MD5 | 80439519120ab80a63e7eab5ce6f82d5 |
|
| BLAKE2b-256 | c7913625189b8df8aa7ad7e2ae3a335433dd9ee8a00cd45464b593fca5516954 |











