Mass ratio variance-based outlier factor (MOF)
Project description
pymof
Updated by Mr. Supakit Sroynam (6534467323@student.chula.ac.th) and Krung Sinapiromsaran (krung.s@chula.ac.th)
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University
Version 0.2: 23 September 2024
Version 0.3: 9 October 2024
Mass-ratio-variance based outlier factor
Latest news
- Reimplement MOF() to handle datasize about 10,000 data points.
- Implementing MAOF() from the paper "Mass-Ratio-Average-Absolute-Deviation Based Outlier Factor in 2024.
- Documents are editted with more examples.
Introduction
An outlier in a finite dataset is a data point that stands out from the rest. It is often isolaed, unliked normal data points, which tend to cluster together. To identify outliers, the Mass-ratio-variance based Outlier Factor (MOF) was developed and implemented. MOF works by calculating a score of each data point based on the density of itself with respect to other data points. Outliers always have fewer nearby data points so their mass-ratio (a density ratio if the same volumes are used) will be different from normal points. This MOF algorithm does not require any extra settings.
Citation
If you use this package in your research, please consider citing these two papers.
BibTex for the package:
@inproceedings{changsakul2021mass,
title={Mass-ratio-variance based Outlier Factor},
author={Changsakul, Phichapop and Boonsiri, Somjai and Sinapiromsaran, Krung},
booktitle={2021 18th International Joint Conference on Computer Science and Software Engineering (JCSSE)},
pages={1--5},
year={2021},
organization={IEEE}
}
@INPROCEEDINGS{10613697,
author={Fan, Zehong and Luangsodsai, Arthorn and Sinapiromsaran, Krung},
booktitle={2024 21st International Joint Conference on Computer Science and Software Engineering (JCSSE)},
title={Mass-Ratio-Average-Absolute-Deviation Based Outlier Factor for Anomaly Scoring},
year={2024},
volume={},
number={},
pages={488-493},
keywords={Industries;Software algorithms;Process control;Quality control;Nearest neighbor methods;Fraud;Computer security;Anomaly scoring;Statistical dispersion;Mass-ratio distribution;Local outlier factor;Mass-ratio variance outlier factor},
doi={10.1109/JCSSE61278.2024.10613697}}
Installation
To install pymof, type the following command in the terminal
pip install pymof # normal install
pip install --upgrade pymof # or update if needed
Use on jupyter notebook
To make sure that the installed package can be called. A user must include the package path before import as
import sys
sys.path.append('/path/to/lib/python3.xx/site-packages')
Required Dependencies :
- Python 3.9 or higher
- numpy>=1.23
- numba>=0.56.0
- scipy>=1.8.0
- scikit-learn>=1.2.0
- matplotlib>=3.5
Documentation
Mass-ratio-variance based Outlier Factor (MOF)
The outlier score of each data point is calculated using the Mass-ratio-variance based Outlier Factor (MOF). MOF quantifies the global deviation of a data point's density relative to the rest of the dataset. This global perspective is crucial because an outlier's score depends on its overall isolation from all other data points. By analyzing the variance of the mass ratio, MOF can effectively identify data points with significantly lower density compared to their neighbors, indicating their outlier status.
MOF()
Initialize a model object
MOF
Parameters :
Return :
self : object
object of MOF model
MOF.fit(Data, Window = 10000)
Fit data to
MOFmodel
Parameters :
Data : numpy array of shape (n_points, d_dimensions)
The input samples.
Window : integer (int)
window size for calculation.
default window size is 10000.
Return :
self : object
fitted estimator
MOF.visualize()
Visualize data points with
MOF's scores
Note cannot visualize data points having a dimension greather than 3
Parameters :
Return :
decision_scores_ : numpy array of shape (n_samples)
decision score for each point
MOF attributes
| Attributes | Type | Details |
|---|---|---|
| MOF.Data | numpy array of shape (n_points, d_dimensions) | input data for scoring |
| MOF.decision_scores_ | numpy array of shape (n_samples) | decision score for each point |
Sample usage
# This example is from MOF paper.
import numpy as np
import matplotlib.pyplot as plt
data = np.array([[0.0, 1.0], [1.0, 1.0], [2.0, 1.0], [3.0, 1.0],
[0.0, 0.0], [1.0, 0.0], [2.0, 0.0], [3.0, 0.0],
[0.0,-1.0], [1.0,-1.0], [2.0,-1.0], [3.0,-1.0], [8.0, 4.0]
])
model = MOF()
model.fit(data)
scores = model.decision_scores_
print(scores)
model.visualize()
# Create a figure and axes
fig, ax = plt.subplots()
data = model.MassRatio
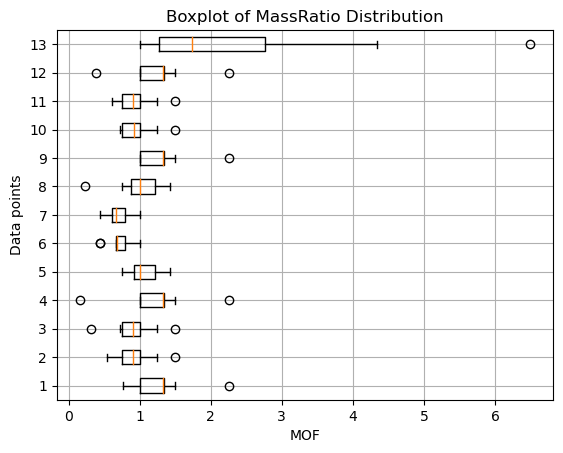
# Iterate over each row and create a boxplot
for i in range(data.shape[0]):
row = data[i, :]
mask = np.isnan(row)
ax.boxplot(row[~mask], positions=[i + 1], vert=False, widths=0.5)
# Set labels and title
ax.set_xlabel("MOF")
ax.set_ylabel("Data points")
ax.set_title("Boxplot of MassRatio distribution")
# Show the plot
plt.grid(True)
plt.show()
Output
[0.12844997, 0.06254347, 0.08142683, 0.20940997, 0.03981233, 0.0212412 , 0.025438 , 0.08894882, 0.11300615, 0.0500218, 0.05805704, 0.17226989, 2.46193377]
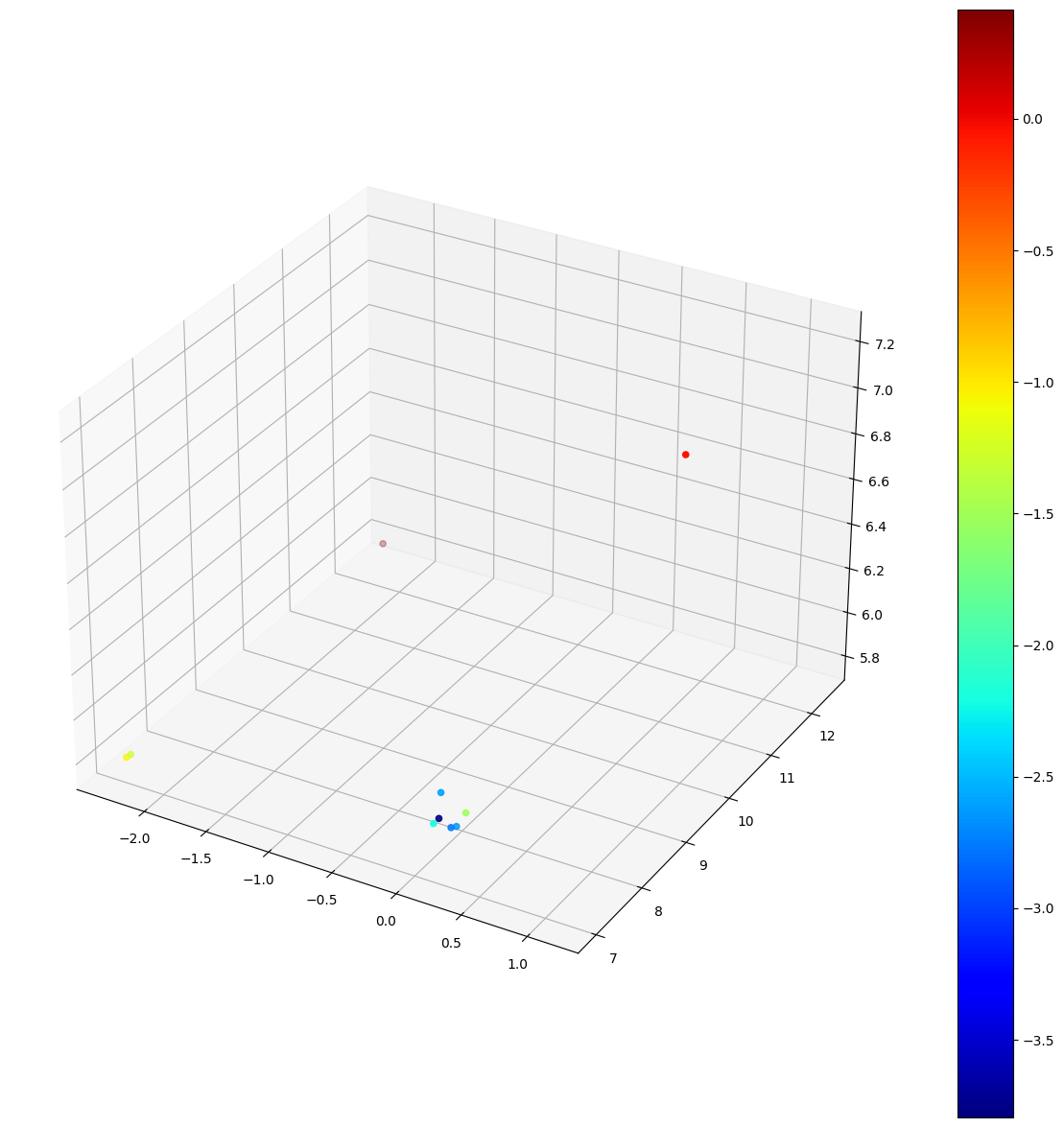
3D sample
# This example demonstrates the usage of MOF
import numpy as np
from pymof import MOF
data = np.array([[-2.30258509, 7.01040212, 5.80242044],
[ 0.09531018, 7.13894636, 5.91106761],
[ 0.09531018, 7.61928251, 5.80242044],
[ 0.09531018, 7.29580291, 6.01640103],
[-2.30258509, 12.43197678, 5.79331844],
[ 1.13140211, 9.53156118, 7.22336862],
[-2.30258509, 7.09431783, 5.79939564],
[ 0.09531018, 7.50444662, 5.82037962],
[ 0.09531018, 7.8184705, 5.82334171],
[ 0.09531018, 7.25212482, 5.91106761]])
model = MOF()
model.fit(data)
scores = model.decision_scores_
print(scores)
model.visualize()
Output
[0.34541068 0.11101711 0.07193073 0.07520904 1.51480377 0.94558894 0.27585581 0.06242823 0.2204504 0.02247725]
Mass-Ratio-Average-Absolute-Deviation Based Outlier Factor (MAOF)
Mass-Ratio-Average-Absolute-Deviation Based Outlier Factor for Anomaly Scoring (MAOF) This research extends the mass-ratio-variance outlier factor algorithm (MOF) by exploring other alternative statistical dispersion beyond the traditional variance such as range, interquartile range, average absolute deviation, and combination of previous two dispersions.
MAOF()
Initialize a model object
MAOF
Parameters :
Return :
self : object
object of MAOF model
MAOF.fit(Data, Window = 10000, Function_name = "AAD", Weight_Lambda = 0.5)
Fit data to
MAOFmodel
Parameters :
Data : numpy array of shape (n_points, d_dimensions)
The input samples.
Window : int
number of points for each calculation.
default window size is 10000.
Function_name : string
A type of statistical dispersion that use for scoring.
Function_name can be 'AAD','IQR', 'Range','Weight'.
default function is 'AAD'
Weight_Lambda : float
0.0 <= Weight_Lambda <= 1.0
A Value of lambda that use in weight-scoring function.
score = λ AAD + (1- λ) IQR
default weight is 0.5
Return :
self : object
fitted estimator
MAOF attributes
| Attributes | Type | Details |
|---|---|---|
| MAOF.Data | numpy array of shape (n_points, d_dimensions) | input data for scoring |
| MAOF.decision_scores_ | numpy array of shape (n_samples) | decision score for each point |
Sample usage
# This example demonstrates the usage of MAOF
from pymof import MAOF
import numpy as np
data = np.array([[-2.30258509, 7.01040212, 5.80242044],
[ 0.09531018, 7.13894636, 5.91106761],
[ 0.09531018, 7.61928251, 5.80242044],
[ 0.09531018, 7.29580291, 6.01640103],
[-2.30258509, 12.43197678, 5.79331844],
[ 1.13140211, 9.53156118, 7.22336862],
[-2.30258509, 7.09431783, 5.79939564],
[ 0.09531018, 7.50444662, 5.82037962],
[ 0.09531018, 7.8184705, 5.82334171],
[ 0.09531018, 7.25212482, 5.91106761]])
model = MAOF()
model.fit(data)
scores = model.decision_scores_
print(scores)
Output
[0.46904762 0.26202234 0.2191358 0.22355477 0.97854203 0.79770723 0.40823045 0.20513423 0.38110915 0.12616108]
Windowing mass-ratio-variance based outlier factor (SMOF)
This algorithm is an extension of the mass-ratio-variance outlier factor algorithm (MOF). WMOF operates on overlapping windows of fixed size, specified by the user. The use of overlapping windows ensures that anomalies occurring at window boundaries are not missed. For each window, the MOF score is computed for all data points within the window.
SMOF()
Initialize a model object
SMOF
Parameters :
Return :
self : object
object of SMOF model
SMOF.fit(Data, Window = 1000, Overlap_ratio = 0.2)
Fit data to
SMOFmodel
Parameters :
Data : numpy array of shape (n_samples, n_features)
The input samples.
Window : integer (int)
number of points for each calculation
default window size is 1000.
Overlap_ratio : float
0.0 <= Overlap_ratio <= 0.5
A Overlap_ratio between window frame.
default ratio is 0.2
Return :
self : object
fitted estimator
SMOF.detectAnomaly(theshold)
Detect data points that have
SMOFscore greater than theshold value
Parameters :
theshold : float
A theshold value for detect anomaly points
Return :
idx : numpy array of shape (n_samples,)
An index array of anomaly ponts in data
SMOF attributes
| Attributes | Type | Details |
|---|---|---|
| MAOF.Data | numpy array of shape (n_points, d_dimensions) | input data for scoring |
| MAOF.decision_scores_ | numpy array of shape (n_samples) | decision score for each point |
| MAOF.Anomaly | numpy array | index of anomaly points in data |
Sample usage
# This example demonstrates the usage of MAOF
from pymof import SMOF
import numpy as np
data = np.array([[-2.30258509, 7.01040212, 5.80242044],
[ 0.09531018, 7.13894636, 5.91106761],
[ 0.09531018, 7.61928251, 5.80242044],
[ 0.09531018, 7.29580291, 6.01640103],
[-2.30258509, 12.43197678, 5.79331844],
[ 1.13140211, 9.53156118, 7.22336862],
[-2.30258509, 7.09431783, 5.79939564],
[ 0.09531018, 7.50444662, 5.82037962],
[ 0.09531018, 7.8184705, 5.82334171],
[ 0.09531018, 7.25212482, 5.91106761]])
model = SMOF()
model.fit(data)
scores = model.decision_scores_
print(scores)
anomaly = model.detectAnomaly(0.8)
print(anomaly)
Output
[0.34541068 0.11101711 0.07193073 0.07520904 1.51480377 0.94558894 0.27585581 0.06242823 0.2204504 0.02247725]
[4 5]
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file pymof-0.4.0.tar.gz.
File metadata
- Download URL: pymof-0.4.0.tar.gz
- Upload date:
- Size: 11.3 kB
- Tags: Source
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 18baa494943893d14fa13b63b7a08a1e44c402b32724822e12ec973e9827e235 |
|
| MD5 | 8c892368707dc12cd14e7b626288da57 |
|
| BLAKE2b-256 | 20384a5c45c40791e1c78d1c3228290d972df6692e7b32e1b385245bed69088e |
File details
Details for the file pymof-0.4.0-py3-none-any.whl.
File metadata
- Download URL: pymof-0.4.0-py3-none-any.whl
- Upload date:
- Size: 10.6 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | f3358fec8beecd14356e684cd4443e4df6c18a8f61e5b9006ebe3e393aee12c8 |
|
| MD5 | 45b6c607e192cb2e4cdac9317e150d8f |
|
| BLAKE2b-256 | 5b02fb77a95a8dfd9a075492c4d5e36031e3318754037fdcd6212065f9542bae |