QRogue is an educational Quantum Computing puzzle game inspired by the classical game Rogue.
Project description
QRogue v0.8.1

Table of Contents
- About the Game
- Game World
- Quantum Puzzles
- Feedback
- Installation
- Dependencies
- Linux/macOS
- Windows
- Notes
- Playing the Game
- Terminal
- Launch Options
- Controls
- Difficulty Modes
- Main Menu
- Screen check
- Pause Menu
- Mathematical Background
- Quantum Bits
- Quantum Operations
- Applying Operations in series
- Working with multiple Qubits
- Applying Operations in parallel
- References
About the Game: A Journey through a Universe full of Quantum Computing!
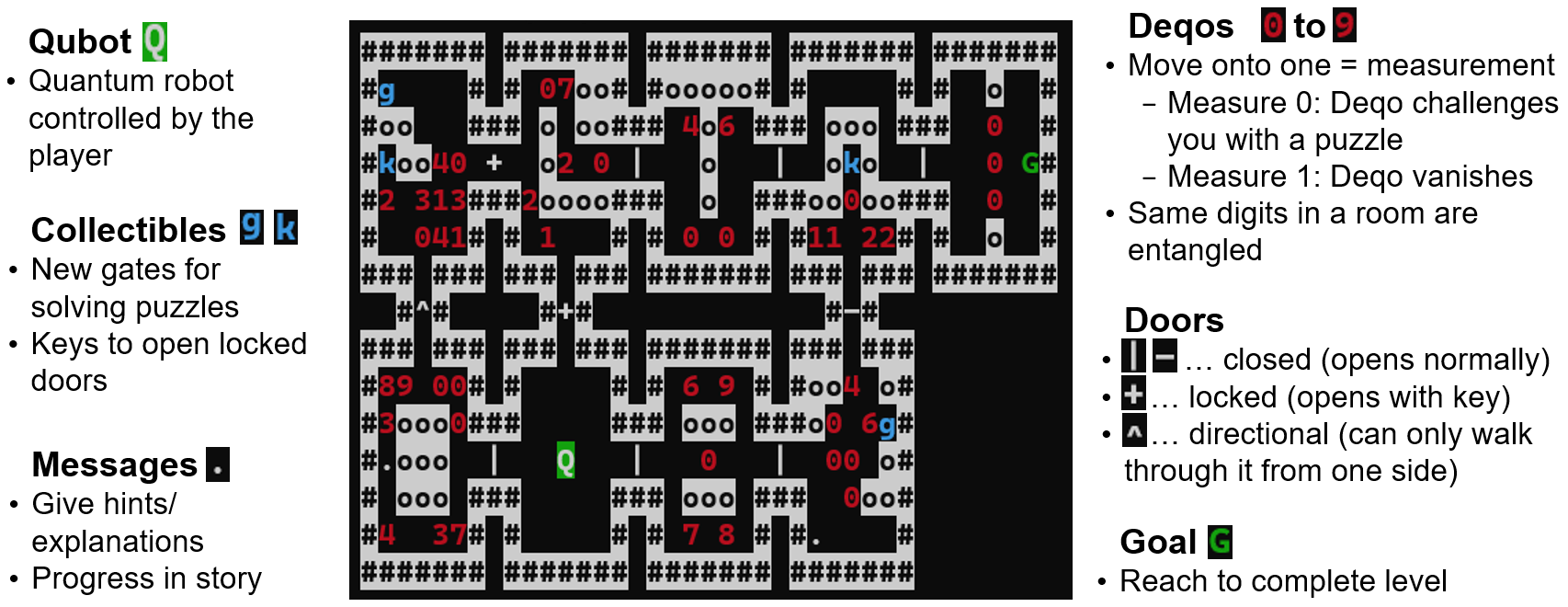
QRogue is an educational game about Quantum Computing, inspired in look and feel by the 1980s released classical game Rogue. You will play as a student who's dreaming about traveling the galaxy. As you hear about "Mission Quniverse", you immediately apply for its training program to be able to join this fascinating Quantum Computing powered universe exploration mission. In the lessons of the training program and later on during expeditions of Mission Quniverse you will come across a variety of quantum gates. Your Qubot - a robot you control to manipulate quantum circuits - will be able to use them to steadily increase its capabilities and even design small scale quantum algorithms at some point.
But beware of ill-disposed Decoherers - or Deqos for short! They got their name from Decoherence, a phenomenon of the quantum realm that describes how interactions with the environment can destroy a quantum state and turn it classical. And these Deqos will do their best to stand in your way. But luckily, they are in Superposition and your Qubot is equipped with a Measurement ability. This means, you can collapse their quantum state to 0 or 1 by moving towards them. Depending on the result, they will either manifest and block your path until you solve their quantum puzzle, or vanish without a trace. Be ready to combine various quantum gates into all kinds of quantum circuits should you be challenged to solve a puzzle. And some Deqos will be entangled, forming a group that collectively collapses to the same classical state upon measurement.
Game World
The game world of QRogue consists of multiple elements described in Fig. 1.
Quantum Puzzles
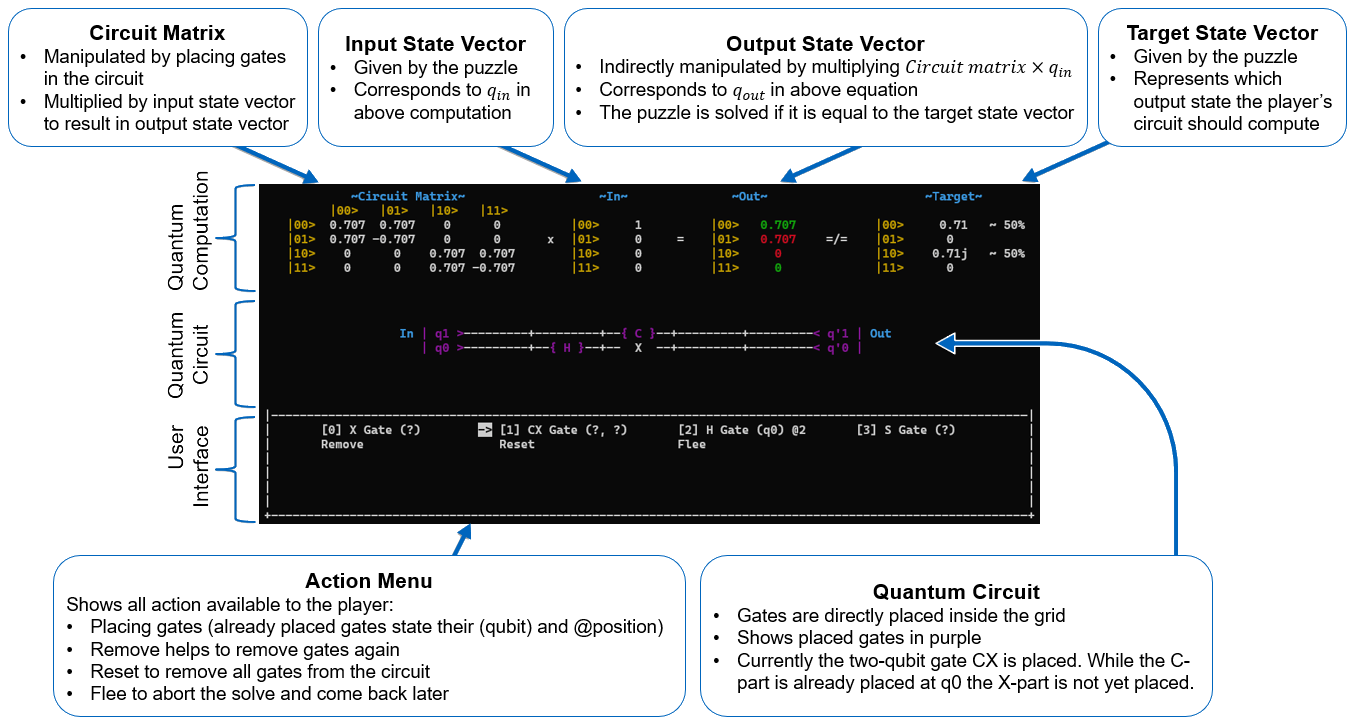
Progress in QRogue is achieved by solving Quantum Puzzles. They consist of a given Input State Vector and Target State Vector. Your goal is to place Quantum Gates in your Quantum Circuit to adjust the corresponding Circuit Matrix until the Output State Vector is equal to the Target State Vector. This is visualized and described in more detail in Fig. 2. Don't worry if it looks confusing at firs, the game will gradually introduce elements and teach you all you need to know. Additionally, there is a description further down in the Section "Mathematical Background".
Feedback
We'd be very happy if you share any feedback with us, regardless whether you liked the game or not. Just send it via email to qrogue.game@gmail.com with the subject "QRogue Feedback". It would also be nice if you could add your user-data folder ("qrogue/QrogueData", for standard installations it can be found in your virtual environment's packages) with the log files. Thanks!
Installation
Dependencies
- py_cui 0.1.4
- qiskit 0.34.2
- numpy 1.20.3
- antlr4-python3-runtime 4.10
However, these dependencies are installed automatically if you install QRogue via pip.
Linux/macOS
Prerequisites
- Python 3.8
- pip
For Linux/macOS, you simply have to run
pip install qrogue
to install QRogue in your current Python environment.
Afterwards you can launch the game simply by executing qrogue in the Python environment you installed QRogue in.
Windows
Alternatively, you can download a Windows-build from here and simply launch qrogue.exe.
Prerequisites
Same as for Linux/macOS
Notes
py_cui.errors.PyCUIOutOfBoundsError
Should you ever encounter this error when starting the game, please try to maximize the console you use for playing. This is because currently there is no automatic font size adaption, so depending on your console settings a minimum width and height is required. Alternatively, or if maximizing doesn't help, you can also lower the font size of the console.
- newer Python versions
Usually also Python 3.9 should perfectly work for playing QRogue, but testing is currently done for Python 3.8, so there is no official support yet for other versions. The same is true if you decide to manually install the dependencies; newer version will likely work, but are not recommended. Python 3.10 is not yet supported due to changes in import locations.
Playing the Game
Terminal
While the game can be played on any terminal, we developed the game while playing on Windows Terminal with the following settings (should be mostly applicable to other terminals as well):
-
Font
Font face and font size are most important and should be available in all terminals. Don't worry if you cannot adjust font weight or line height.- Font Face = Cascadia Mono
Use a monotype font face because otherwise the game will not be displayed in a straight grid. - Font Size = 13
Depends on used font face and screen size (we used 1920x1080, Full HD). In general, this font size allowed us to display 46 rows and 189 characters per row (more details further down or in the game's Screen check-menu). - Font Weight = Bold
Depends on your specific font face and your preferred look. - Line Height = 1.2 (default value)
Again, font face dependent.
- Font Face = Cascadia Mono
-
Colors
QRogue uses colors to highlight certain words in explanations, objects in the game world or elements of the puzzle screen. The following list is what we used, but can freely be adjusted based on your preferences (although they should be distinguishable from each other, so players have an easy time reading texts, the game world or puzzles - more on that further down in Screen Check).- "red": "#C50F1F"
- "brightRed": "#E74856"
- "green": "#13A10E"
- "brightGreen": "#16C60C"
- "blue": "#0037DA"
- "brightBlue": "#3B78FF"
- "purple": "#881798"
- "brightPurple": "#B4009E"
- "yellow": "#C19C00"
- "cyan": "#3A96DD"
- "black": "#0C0C0C"
- "brightBlack": "#767676"
- "white": "#CCCCCC"
- "brightWhite": "#F2F2F2"
- "foreground": "#CCCCCC"
- "background": "#0C0C0C"
- "cursorColor": "#FFFFFF"
Launch Options
-
--user-data/-ud $path:
Path to the folder where you want to store/load user data (options, save data) from. By default, QRogue will create a new folder in its installation directory. -
--game-data/-gd $path:
Path to the folder where you want to store/load game data (levels, default config, clean save) from. Only specify if you know what you're doing!
For debugging purposes only:
-
--debug/-d:
Activates debug-mode and certain options like additional logs, rendering additional information, cheat codes, simulation of runs, ... -
--from-console/-fc:
Skips the closing prompt when you exit the game. Necessary to see errors if you're not starting the game from a console. -
--validate-map/-vm $path:
Check whether a level can be generated successfully from the given.qrdgfile. -
--test-level/-tl $path:
Specifies a level to play. -
--simulation-path/-sp $path:
Specifies the.qrkl(key log) file to use for simulating a run of the game.
Controls
- Navigate in menus: Arrow Keys, wasd
- Move in game world: Arrow Keys, wasd
- Scroll in popup: Arrow Keys, wasd
- Close popup: Space, Enter
- Reopen last popup: H
- Select answer in question popup: horizontal Arrow Keys, ad
- Confirm selection (also in question popup): Space, Enter
- Cancel/back: Shift+A, Shift+Left, Backspace
- Pause: P, Tab
- Situational
- shortcut keys: 0-9
- Debug Keys (not for use in standard play through!)
- Print screen: CTRL+P
- Force re-render: CTRL+R
Difficulty Modes
The first time you launch the game, you will be asked to choose a difficulty:
-
Quantum Newbie:
The training program will use easier puzzles and explain both game mechanics and Quantum Computing in full detail. Pick this difficulty if you are unsure. -
Quantum Experienced:
The training program will use harder puzzles and only explain game mechanics. Explanations about Quantum Computing can still be read via the in-game manual.
The game does not support adjusting the difficulty. Because after completing the training program (45-60min), both modes behave the exact same way.
Main Menu
On a fresh save, the main menu will have the following options:
-
START YOUR JOURNEY
Starts the training program. Changes toCONTINUEafter completing the first lesson of the training program. -
SCREEN CHECK
See section below for more info. -
SAVE
Saves the game. -
EXIT
Exit the game.
As you progress through the training program, you will unlock the following two options:
-
LEVEL SELECT
Replay completed Lessons or start specific Expeditions, with the option to choose which Quantum Gates you want to bring with you -
WORKBENCH
Manage your Quantum Gates to combine them into new, more complex ones.
Screen Check
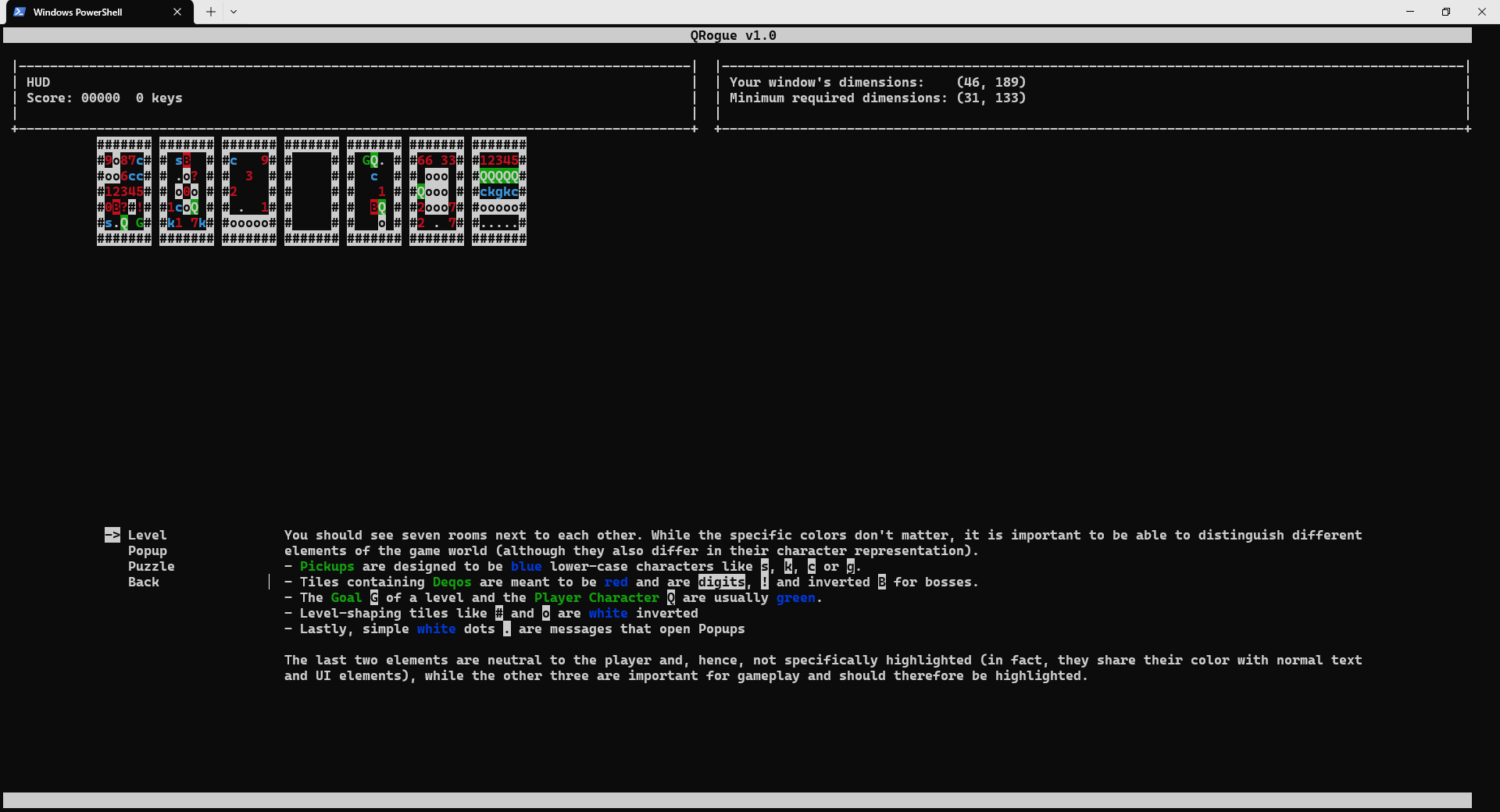
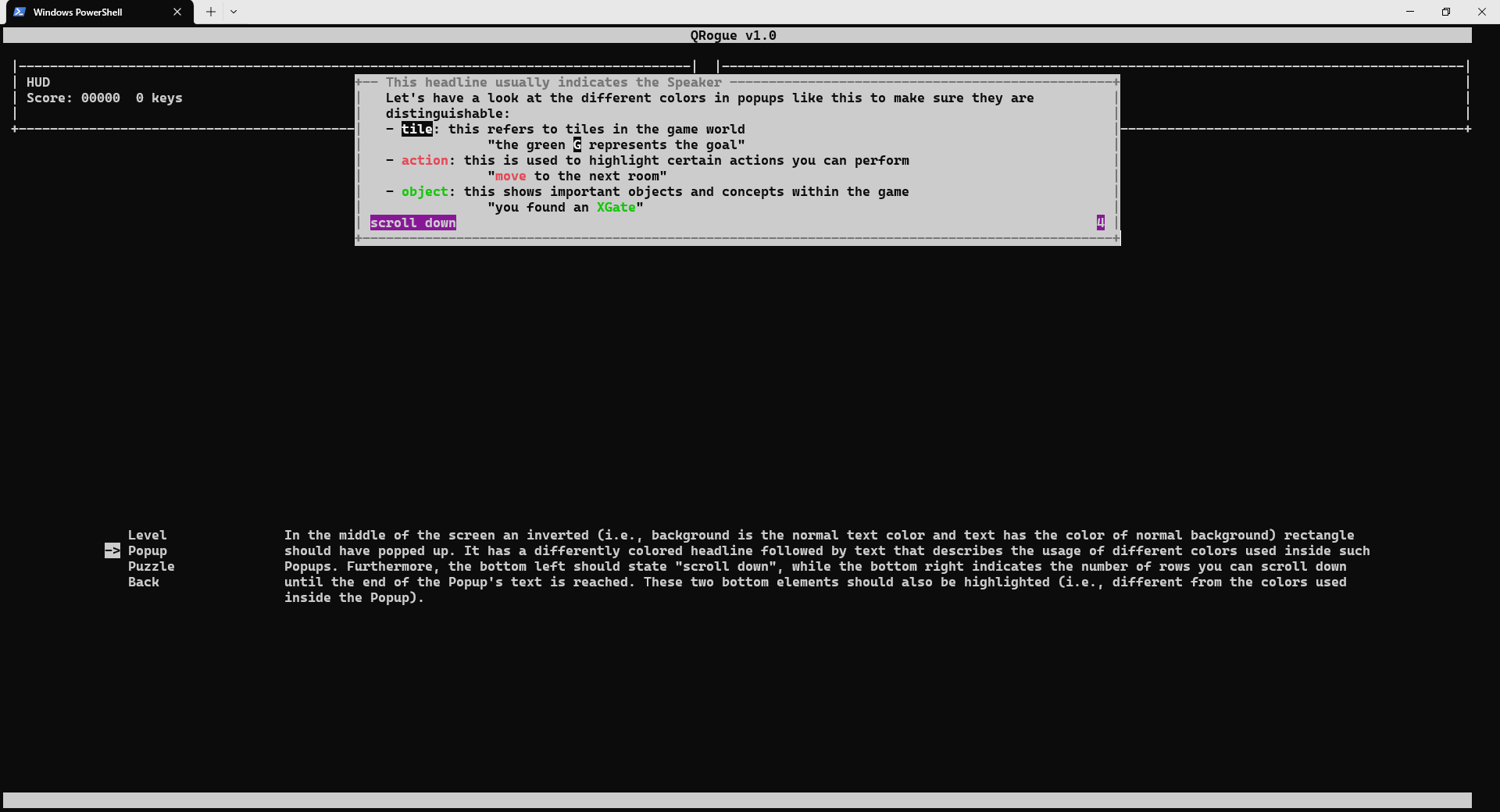
Since QRogue is played in a terminal, it cannot control its exact look. Hence, it is recommended to quickly verify with the screen check-menu if the used colors are distinguishable (see previous Section Terminal→Colors) and, most importantly, your window is big enough. The minimum required window dimensions (referring to the number of rows and the number of characters per row) and the actual window dimensions can be found in the top right.
The texts in the screen check-menu already explain what you should see and be able to distinguish, but here are some screenshots for reference:
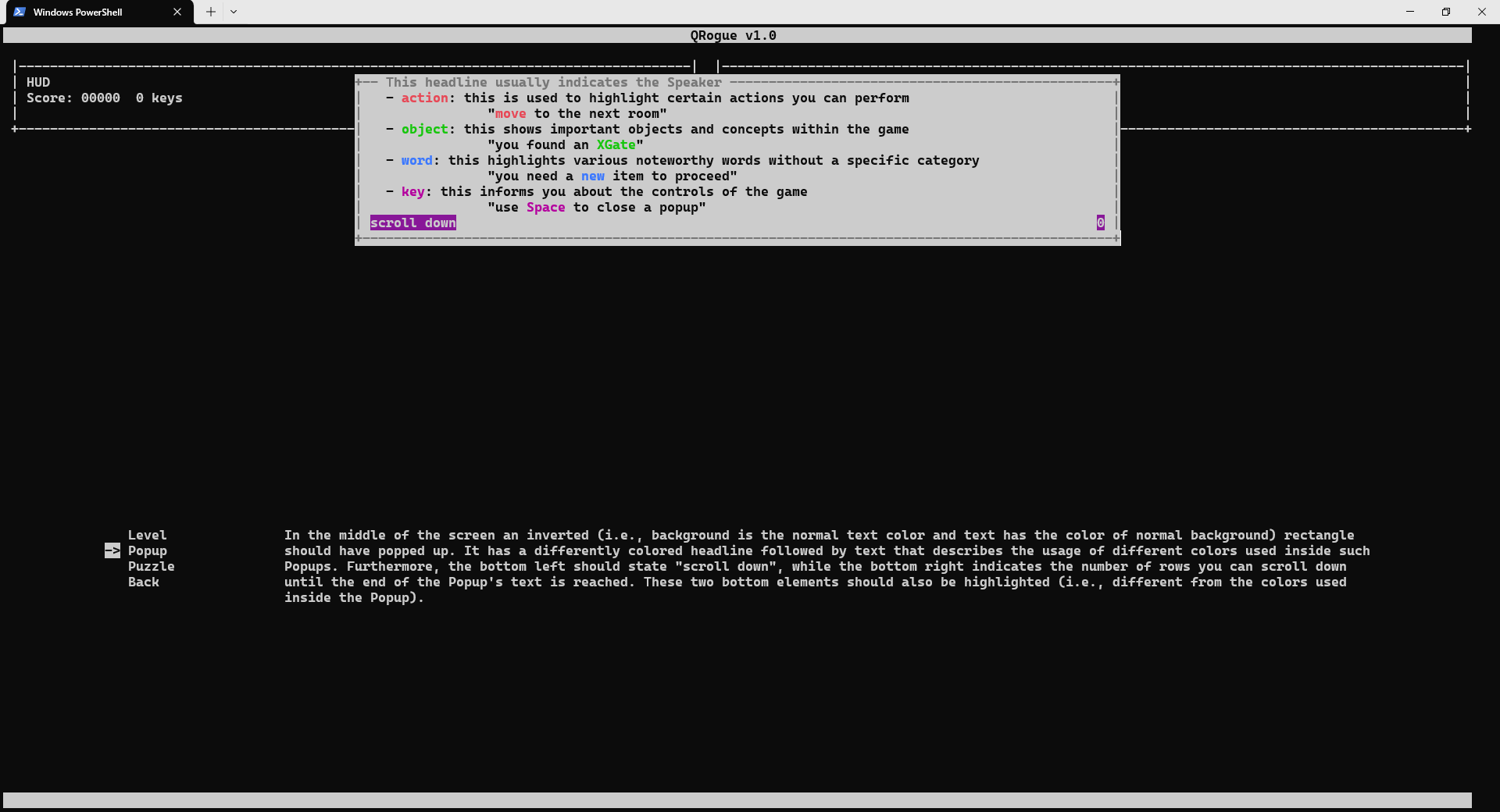
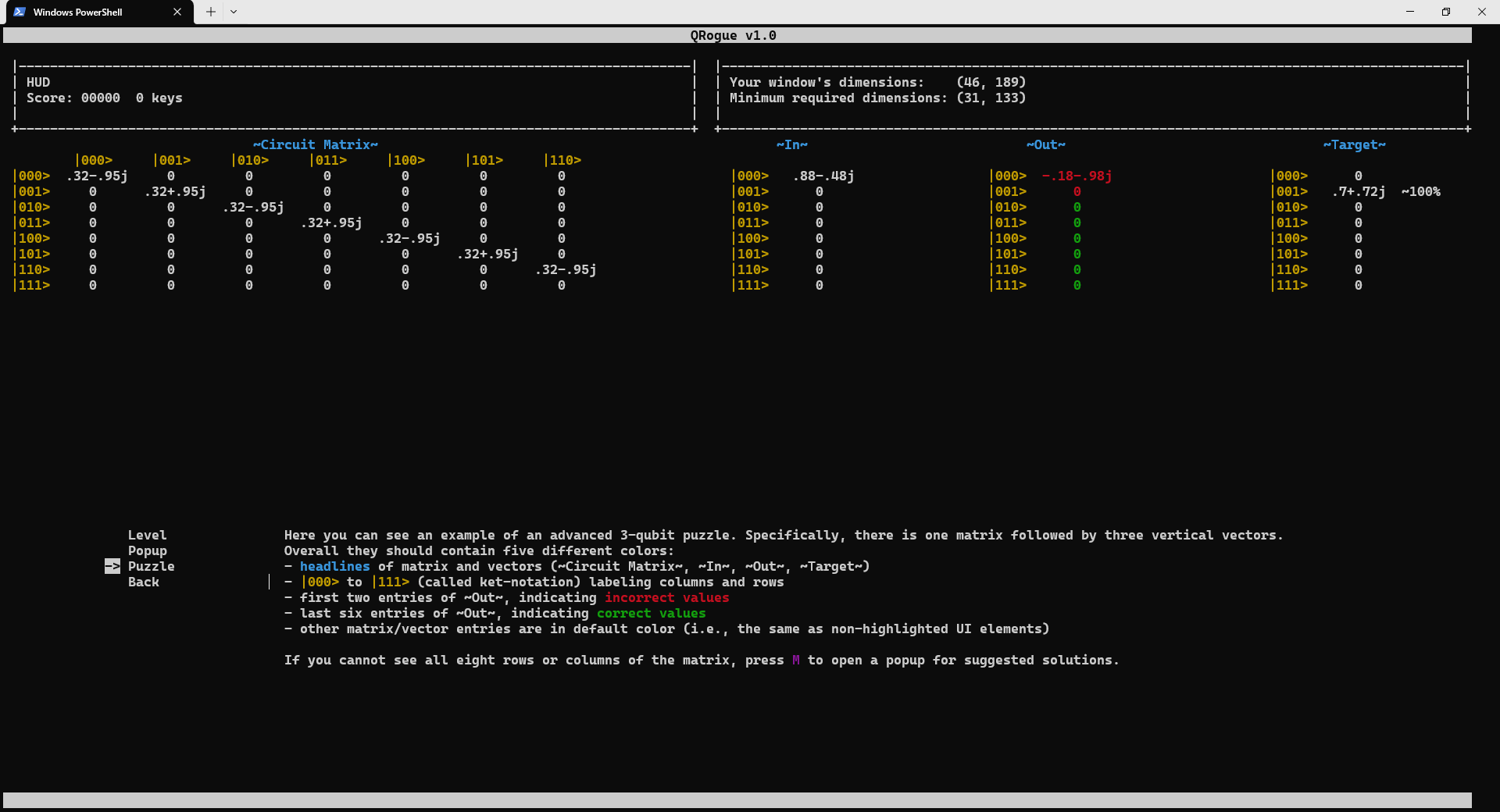
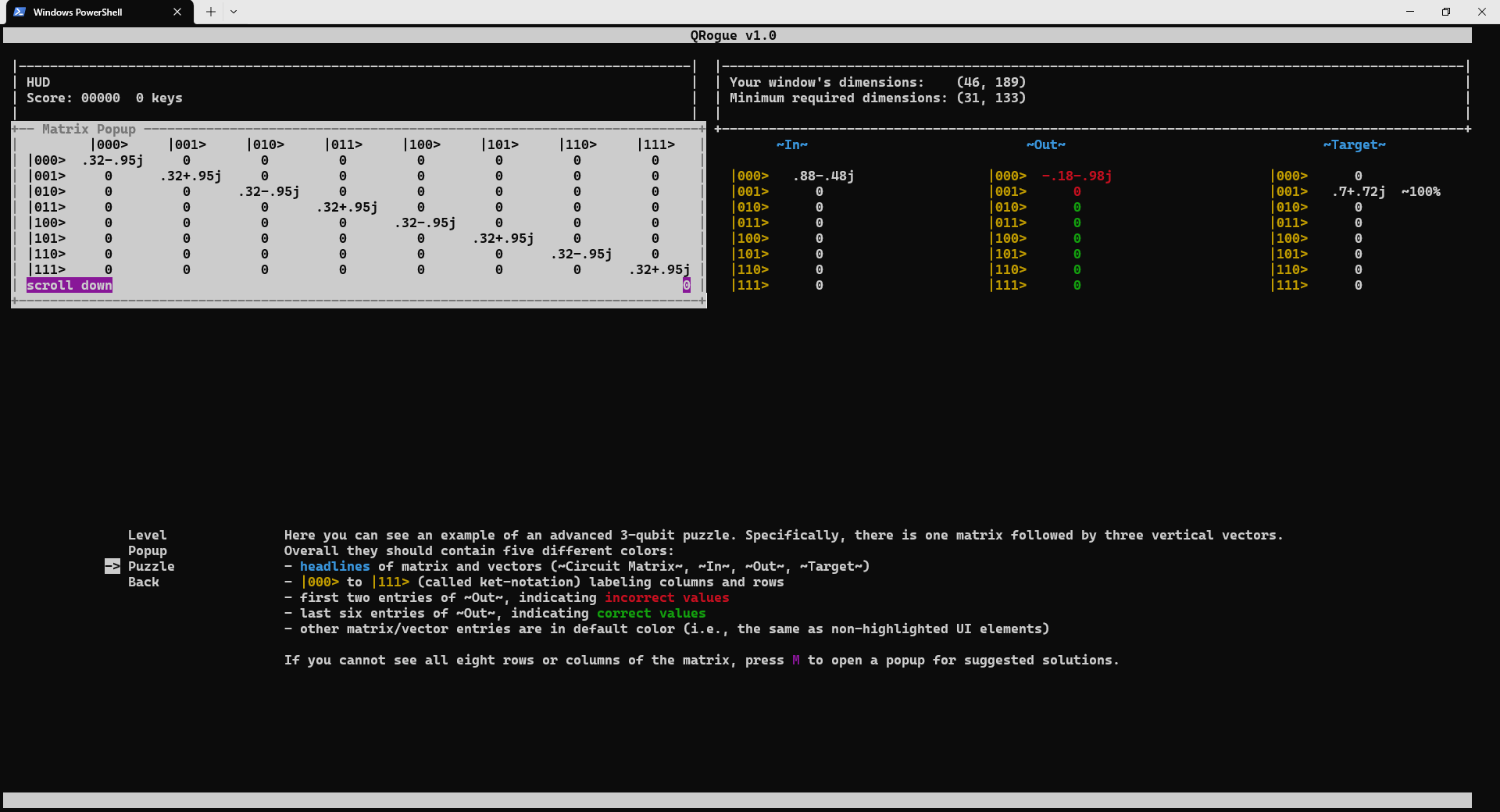
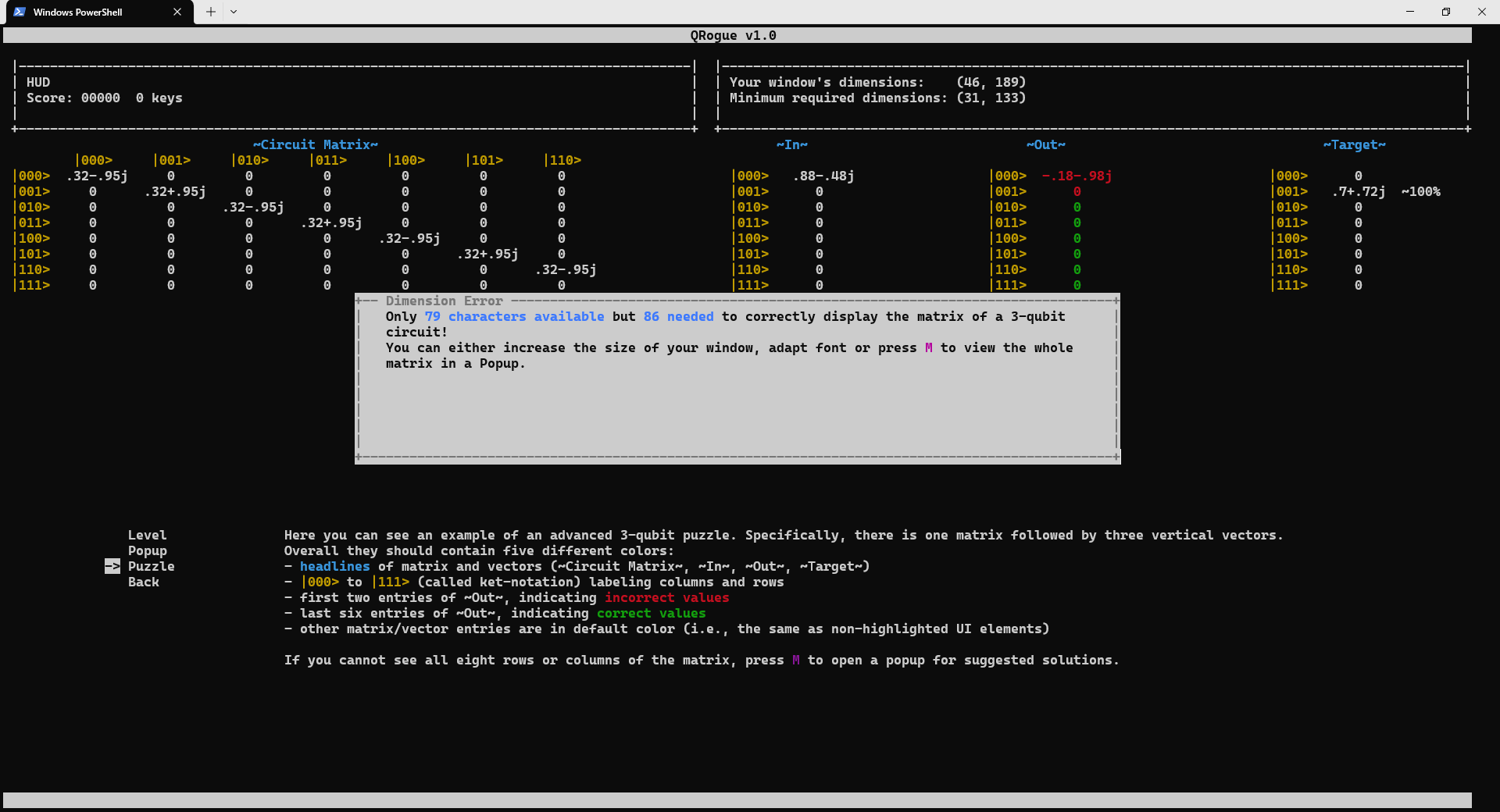
Pause Menu
You can do several things in the Pause Menu:
Continue
Continue from where you opened the Pause Menu.Restart
Re-randomizes puzzles and restarts the current level.Save
Saves the game (only if progress changes since the last save).Manual
An encyclopedia of all things important to play the game.Options
Tweak some options to your liking.Exit
Exit the current level and go back to the Main Menu.
Mathematical background
Quantum computations are the heart of QRogue's puzzles. They boil down to matrix-vector multiplication, whereas states (e.g., input or output state) are described by vectors and operations (i.e., gates) by matrices. To get a glimpse of what this means, we will describe the basics in the following sections.
Quantum Bits
Unlike classical (i.e., electrical) bits, quantum bits can not only be $0$ or $1$ but rather a linear combination of these two classical states. By writing them in ket-notation (${|0>}$ and ${|1>}$, respectively) defined as
{|0>} = \begin{pmatrix} 1\\0\end{pmatrix}
,
{|1>} = \begin{pmatrix} 0\\1\end{pmatrix}
we can introduce so-called amplitudes $\alpha, \beta \in \mathbb{C}$, with ${|\alpha|}^2 + {|\beta|}^2 = 1$ to fully describe the state of any qubit $q_i$ as follows:
q_i = \alpha {|0>} + \beta {|1>} = \begin{pmatrix} \alpha\\0\end{pmatrix} + \begin{pmatrix} 0\\\beta\end{pmatrix} = \begin{pmatrix} \alpha\\\beta\end{pmatrix}.
In case $\alpha \ne 0$ and $\beta \ne 0$ the qubit is in superposition (i.e., a non-classical state where the qubit is both $0$ and $1$ at the same time) whereas $\alpha = 1$ or $\beta = 1$ correspond to the classical states $0$ or $1$, respectively.
Quantum Operations
To conduct computations on qubits QRogue uses quantum gates corresponding to certain quantum operations. All of them can be described by $2^n \times 2^n$ unitary matrices, with $n$ corresponding to the number of qubits the operation is applied to (e.g., single qubit operations have dimensions $2 \times 2$).
Let's take a look at a counterpart to the classical NOT operation (i.e., not $0 = 1$ and not $1 = 0$):
X =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix} .
The effect of applying this operation onto a single qubit $q_0$ can be calculated by matrix-vector multiplication:
{q{'}_{0}} = Gate \times {q_0} = X \times (\alpha{|0>} + \beta{|1>}) =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
\begin{pmatrix} \alpha\\\beta \end{pmatrix}
=
\begin{pmatrix} \beta\\\alpha \end{pmatrix}.
If $q_0$ is in a classical state (e.g., either $\alpha = 1$ or $\beta = 1$) we can easily see that this indeed corresponds to a NOT.
For a second example we consider the Hadamard operation $H$ which is often used to create superposition:
H =
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix} .
Now we assume our qubit $q_0$ is in the classical zero state ${|0>}$ (i.e., $\alpha = 1$ and $\beta = 0$) and we apply the Hadamard operation onto it:
{q{'}_{0}} = H \times {|0>} =
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
\begin{pmatrix} 1\\0\end{pmatrix}
=
\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\1\end{pmatrix}.
As we can see, ${q{'}_{0}}$ is now in superposition and $\alpha = \beta = \frac{1}{\sqrt{2}}$.
In QRogue the last example would correspond to an H Gate being placed on $q_0$ in our quantum circuit like this:
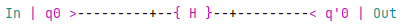
Applying Operations in series
Since we usually want to conduct more than a single operation, we can combine sequentially applied operations by matrix-matrix multiplication:
algorithm_{xh} = H \times X =
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
=
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
-1 & 1
\end{bmatrix}
Again, these two operations can be applied onto the state ${|0>}$:
{q{'}_{0}} = H \times X \times {|0>} = algorithm_{xh} \times {|0>} =
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
-1 & 1
\end{bmatrix}
\begin{pmatrix} 1\\0\end{pmatrix}
=
\frac{1}{\sqrt{2}}\begin{pmatrix} 1\\-1\end{pmatrix}.
This algorithm is equivalent to the following circuit in QRogue:
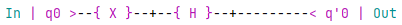
Note that the order of $X$ and $H$ is from left to right in the circuit, while it is from right to left in the multiplication. This is also the reason we denoted it as $algorithm_{xh}$ and not $algorithm_{hx}$.
Working with multiple Qubits
To work with more than a single qubit we first need to extend our state vector. This is done by computing the Kronecker product of two single qubit states:
q_{in} = q_1 \otimes q_0 = \begin{pmatrix} \alpha_1\\\beta_1 \end{pmatrix} \otimes \begin{pmatrix} \alpha_0\\\beta_0 \end{pmatrix} =
\begin{pmatrix} \alpha_1 \times \alpha_0\\ \alpha_1 \times \beta_0 \\ \beta_1 \times \alpha_0 \\ \beta_1 \times \beta_0 \end{pmatrix}.
Alternatively, this can be also written as $q_{in} = (\alpha_1 \times \alpha_0){|00>} + (\alpha_1 \times \beta_0){|01>} + (\beta_1 \times \alpha_0){|10>} + (\beta_1 \times \beta_0){|11>}$.
In case of $q_0 = q_1 = {|0>}$ this results in
q_{in} = q_1 \otimes q_0 = \begin{pmatrix} 1\\ 0\end{pmatrix} \otimes \begin{pmatrix} 1\\ 0\end{pmatrix} =
\begin{pmatrix} 1\\ 0\\ 0\\ 0\end{pmatrix},
corresponding to the classical state ${|00>}$.
To conduct single qubit operations on our two qubit state, we also need to extend the operations via Kronecker products. Luckily, the identity operation $I$ can help us out to apply an operation to a qubit without changing its state. As an example, we apply $H$ onto $q_0$ without influencing $q_1$:
{q_{out}} = {q{'}_{in}} = (I \otimes H) \times (q_1 \otimes q_0) =
(
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\otimes
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
-1 & 1
\end{bmatrix}
) \times q_{in}
= \frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 & 0 & 0 \\
1 & -1 & 0 & 0 \\
0 & 0 & 1 & 1 \\
0 & 0 & 1 & -1
\end{bmatrix}
\times \begin{pmatrix} 1\\ 0\\ 0\\ 0\end{pmatrix} =
\frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 1\\ 0\\ 0\end{pmatrix}
Or alternatively ${q{'}_{in}} = \frac{1}{\sqrt{2}} ({|00>} + {|01>})$ where ${|00>}$ is the combination of states $q_1 = {|0>}, q_0 = {|0>}$ and ${|01>}$ the combination of $q_1 = {|0>}, q_0 = {|1>}$.
This algorithm is equivalent to the following circuit in QRogue:
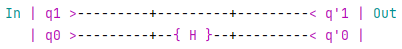
Applying Operations in parallel
Just like we previously extended $H$ with $I$ to be able to apply it to a two qubit state, we can also extend $H$ by another operation. This corresponds to applying these two operations in parallel. When applying $H$ onto $q_0$ and $X$ onto $q_1$, this looks as follows:
algorithm_{hx} = \begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
\otimes
\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1 \\
-1 & 1
\end{bmatrix}
= \frac{1}{\sqrt{2}}
\begin{bmatrix}
0 & 0 & 1 & 1 \\
0 & 0 & 1 & -1 \\
1 & 1 & 0 & 0 \\
1 & -1 & 0 & 0
\end{bmatrix}
Once again, this algorithm corresponds to the following circuit in QRogue:
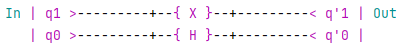
Which is also equivalent to:
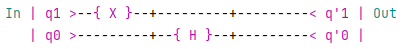
References
-
Short Paper
Presented at FDG2023 conference -
PyPI
Python packages for installation via pip
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file qrogue-0.8.1.3.tar.gz.
File metadata
- Download URL: qrogue-0.8.1.3.tar.gz
- Upload date:
- Size: 292.1 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.8.0
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 684ec7eafe274993750f61cc89e212439015bff7766b6bf3f41b8f45844a8652 |
|
| MD5 | d8fa0e21b29f24b0d6b5318ff103cb16 |
|
| BLAKE2b-256 | 6c8136a40748c2bdd48513ea542284017fa28237f76f8d3d1ac7cf68cd9850c7 |











