Vector Quantile Regression
Project description
vqr: Fast Nonlinear Vector Quantile Regression
This package provides the first scalable implementation of Vector Quantile Regression (VQR), ready for large real-world datasets. In addition, it provides a powerful extension which makes VQR non-linear in the covariates, via a learnable transformation. The package is easy to use via a familiar sklearn-style API.
Refer to our paper[^VQR2022] for further details about nonlinear VQR, and please cite our work if you use this package:
@article{rosenberg2022fast,
title={Fast Nonlinear Vector Quantile Regression},
author={Rosenberg, Aviv A and Vedula, Sanketh and Romano, Yaniv and Bronstein, Alex M},
journal={arXiv preprint arXiv:2205.14977},
year={2022}
}
Brief background and intuition
Quantile regression[^Koenker1978] (QR) is a well-known method which estimates a conditional quantile of a target variable $\text{Y}$, given covariates $\mathbf{X}$. Since a distribution can be exactly specified in terms of its quantile function, estimating all conditional quantiles recovers the full conditional distribution. A major limitation of QR is that it deals with a scalar-valued target variable, while many important applications require estimation of vector-valued responses.
Vector quantiles extend the notion of quantiles to high-dimensional variables [^Carlier2016]. Vector quantile regression (VQR) is the estimation of the conditional vector quantile function $Q_{\mathbf{Y}|\mathbf{X}}$ from samples drawn from $P_{(\mathbf{X},\mathbf{Y})}$, where $\mathbf{Y}$ is a $d$-dimensional target variable and $\mathbf{X}$ are $k$-dimensional covariates ("features").
VQR is a highly general approach, as it allows for assumption-free estimation of the conditional vector quantile function, which is a fundamental quantity that fully represents the distribuion of $\mathbf{Y}|\mathbf{X}$. Thus, VQR is applicable for any statistical inference task, i.e., it can be used to estimate any quantity corresponding to a distribution.
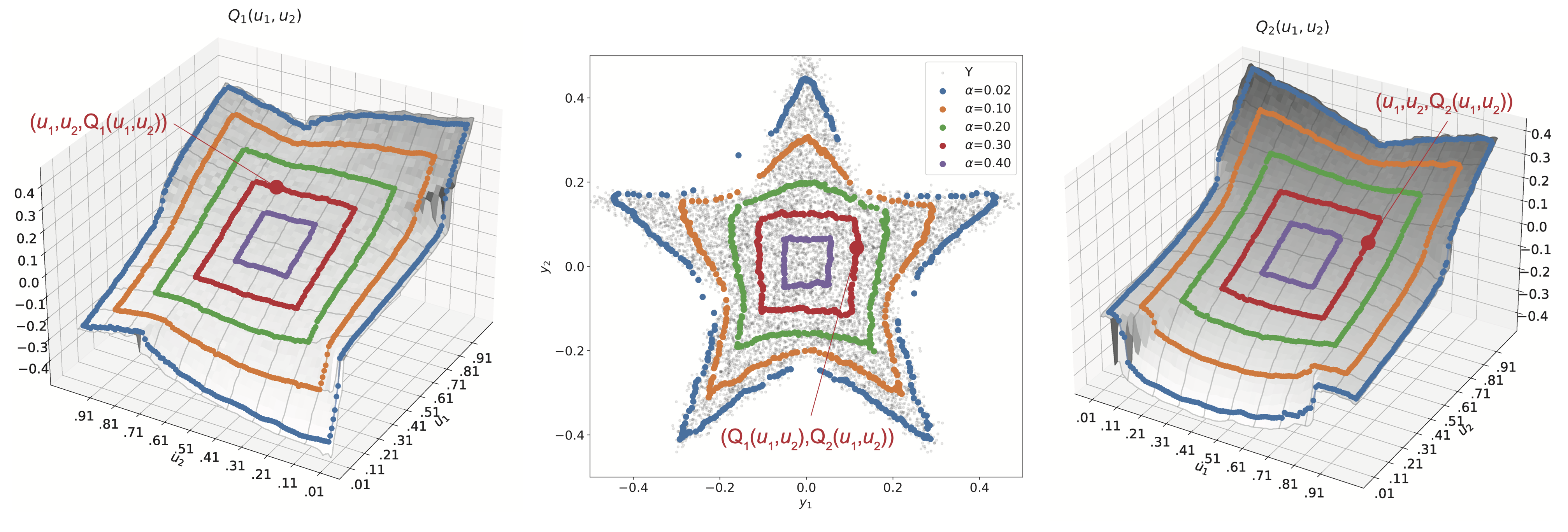
Below is an illustration of vector quantiles of a $d=2$-dimensional star-shaped distribution, where $T=50$ quantile levels were estimated in each dimension.
- Data is sampled uniformly from a 2d star-shaped region (middle, gray dots).
- Vector quantiles are overlaid on their data distribution (middle, colored dots).
- The vector quantile function (VQF) $Q_{\mathbf{Y}}: [0,1]^d \mapsto \mathbb{R}^d$ is a mapping, which satisfies:
- Strong representation: $\mathbf{Y}=Q_{\mathbf{Y}}(\mathbf{U})$ where $\mathbf{U}\sim\mathbb{U}[0,1]^d$.
- Co-monotonicity: $(Q_{\mathbf{Y}}(\boldsymbol{u})-Q_{\mathbf{Y}}(\boldsymbol{u}'))^{\top}(\boldsymbol{u}-\boldsymbol{u}')\geq 0$.
- Different colors correspond to $\alpha$-contours, each containing $100\cdot(1-2\alpha)^d$ percent of the data, a generalization of confidence intervals for vector-valued variables.
- For example, for $\alpha=0.02$, roughly 92% of the data is contained within the contour.
- The shape of the distribution is correctly modelled, without any distributional assuptions.
- For $Q_{\mathbf{Y}}(\boldsymbol{u})=[Q_1(\boldsymbol{u}),Q_2(\boldsymbol{u})]^{\top}$ and $\boldsymbol{u}=(u_1,u_2)$, the components $Q_1, Q_2$ of the VQF are depicted as surfaces (left, right) with the corresponding vector quantiles overlaid.
- On $Q_1$, increasing $u_1$ for a fixed $u_2$ produces a monotonically increasing curve.
- This corresponds to a quantile function for $\text{Y}_1$ given that $\text{Y}_2$ is at a value corresponding to its $u_2$-th quantile (and vice versa for $Q_2$).
Results and Comparisons
Non-linear VQR
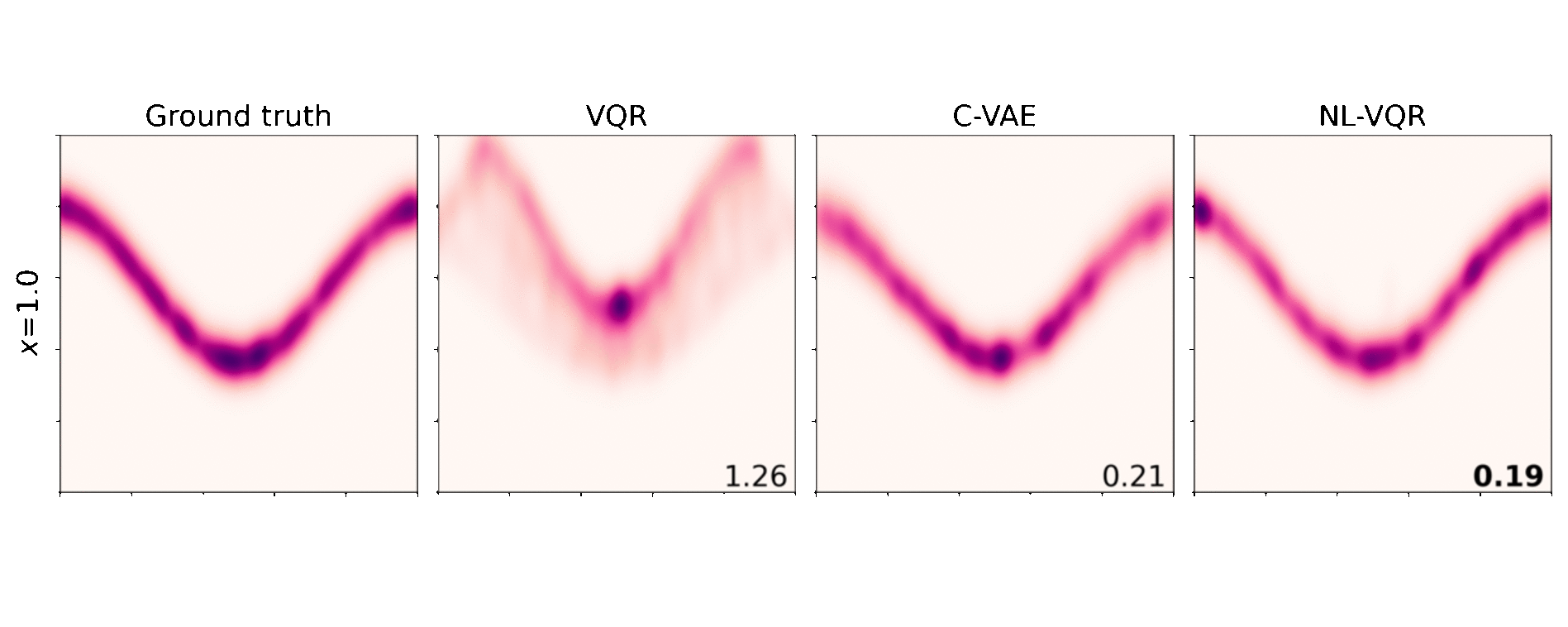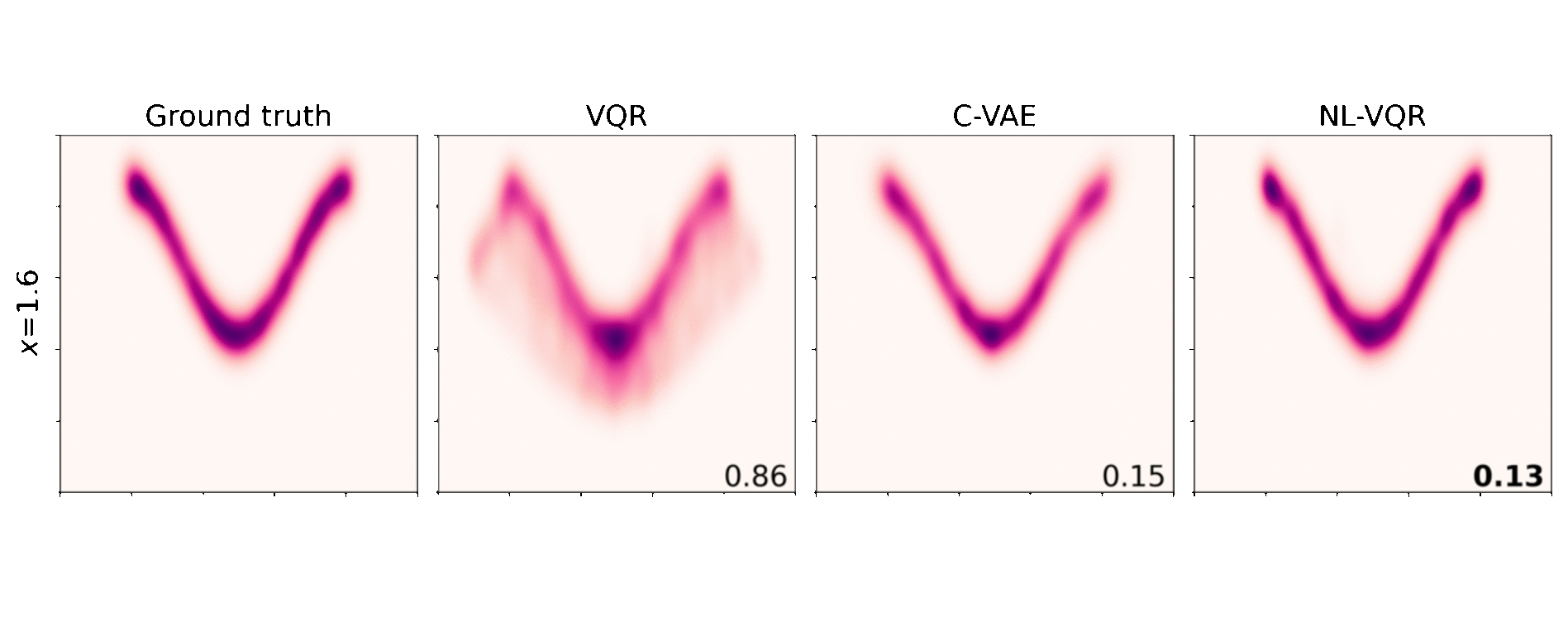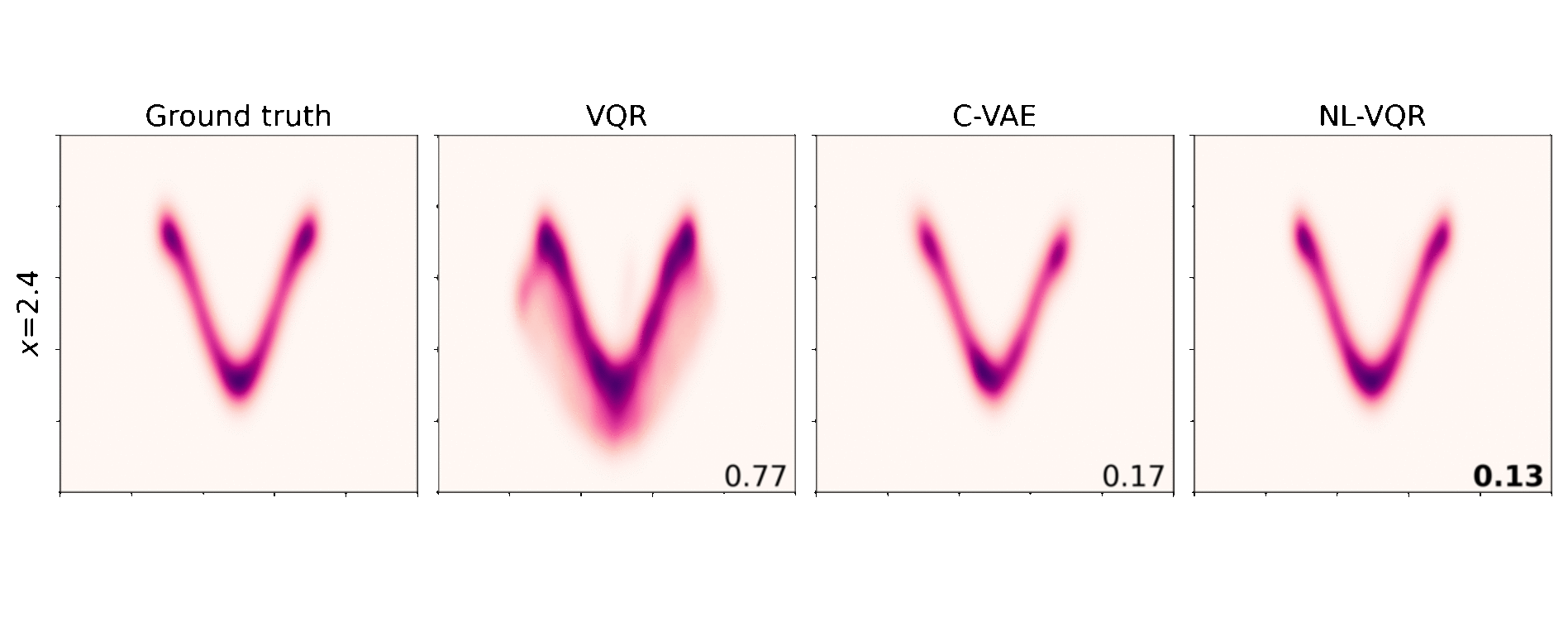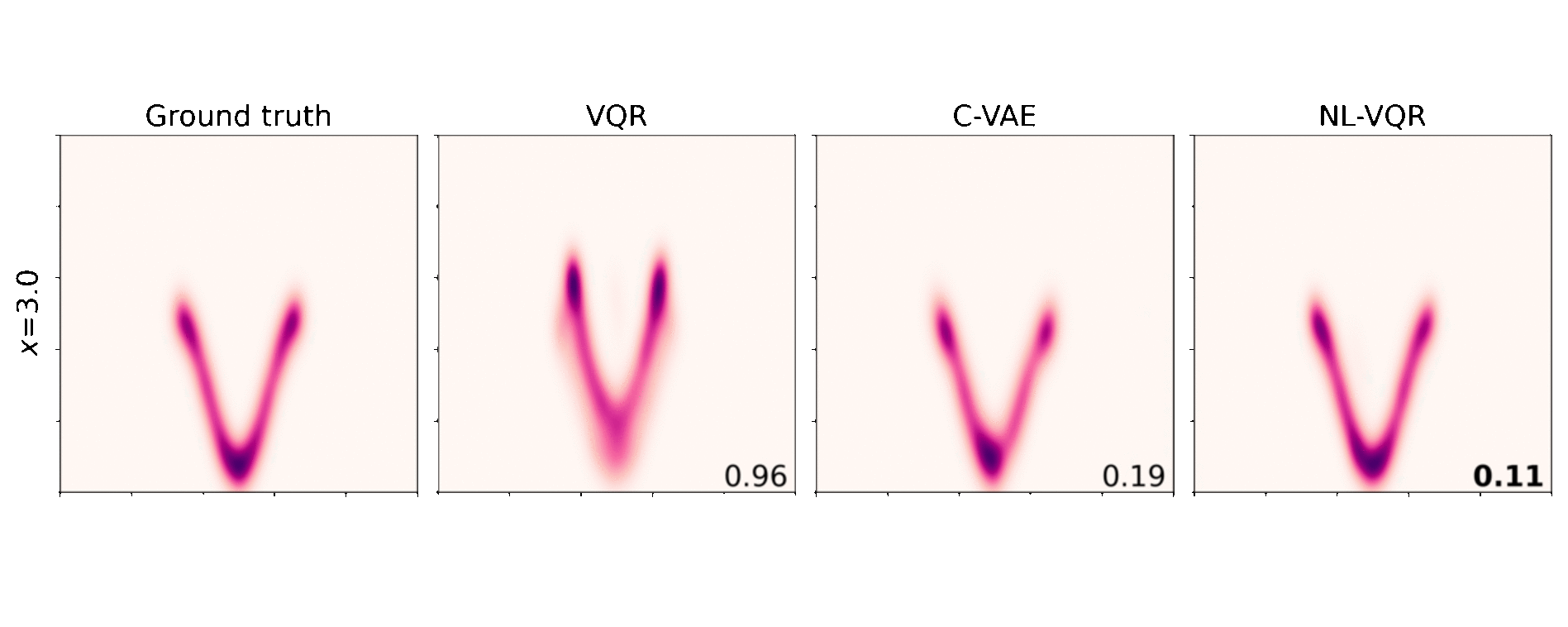
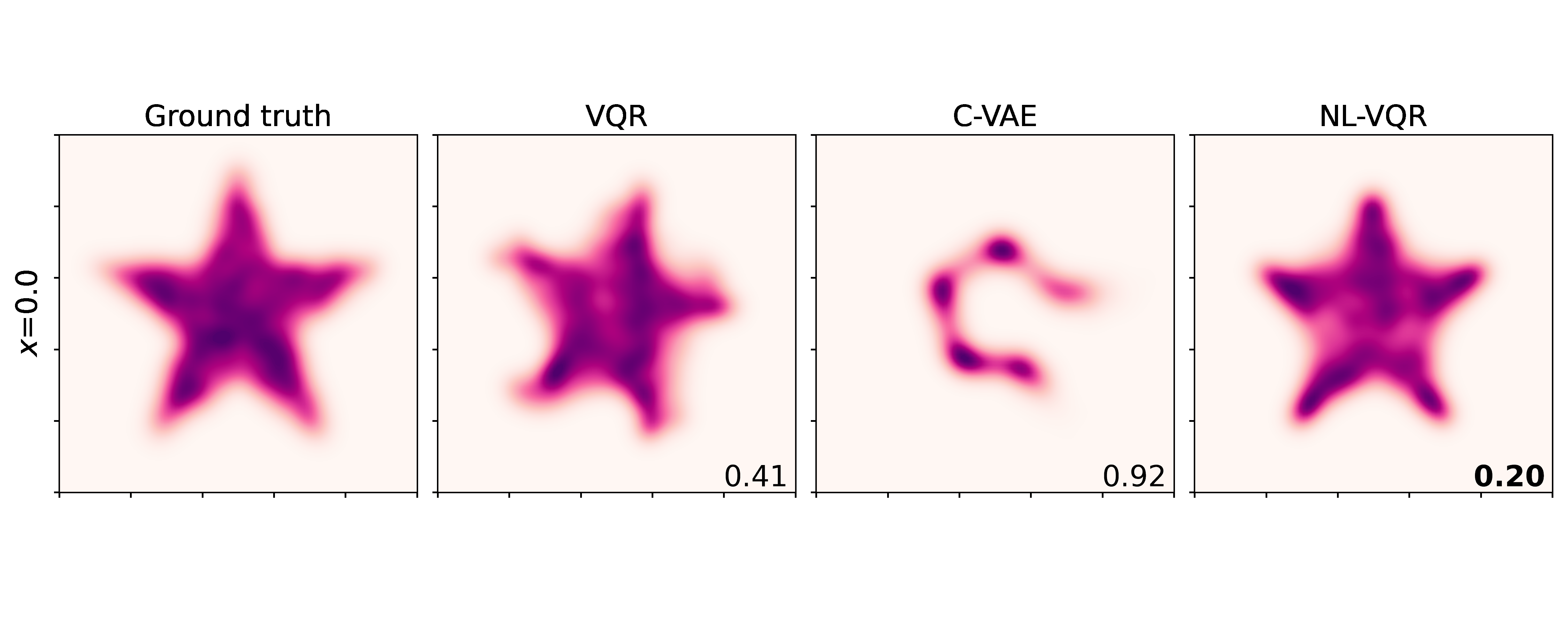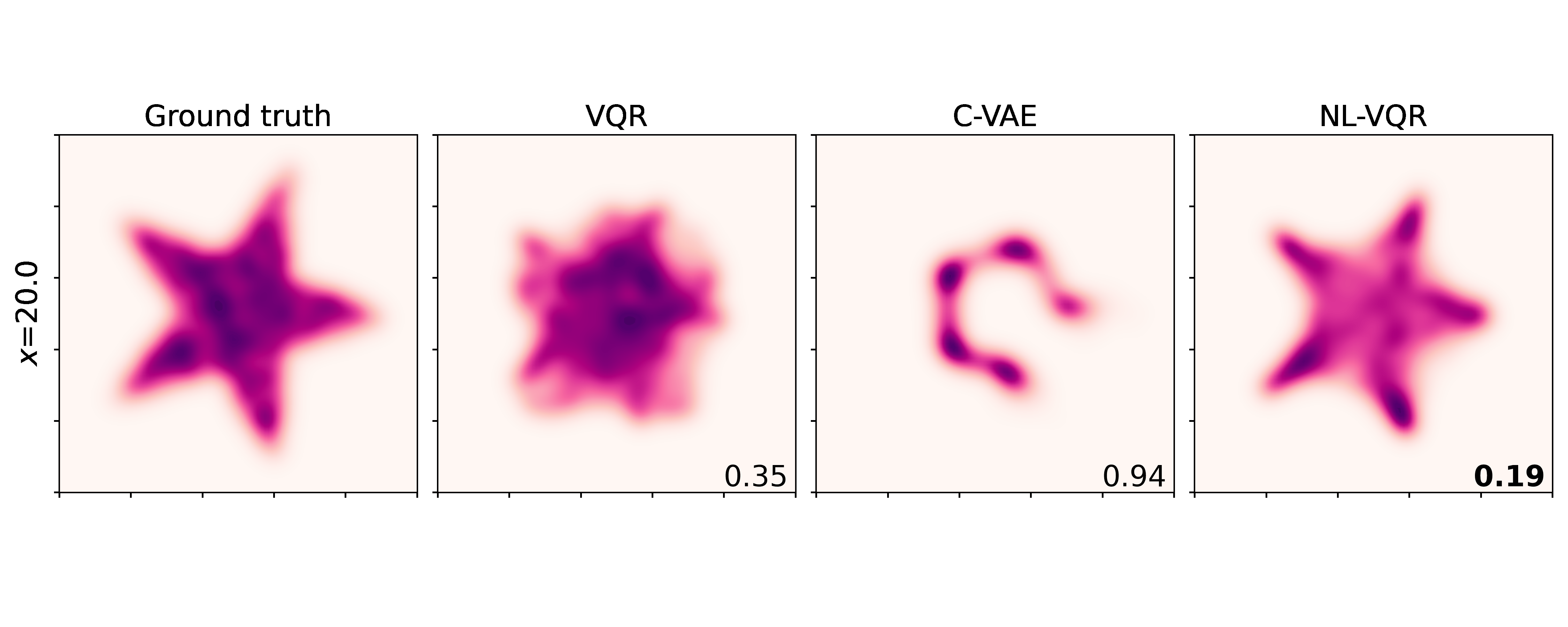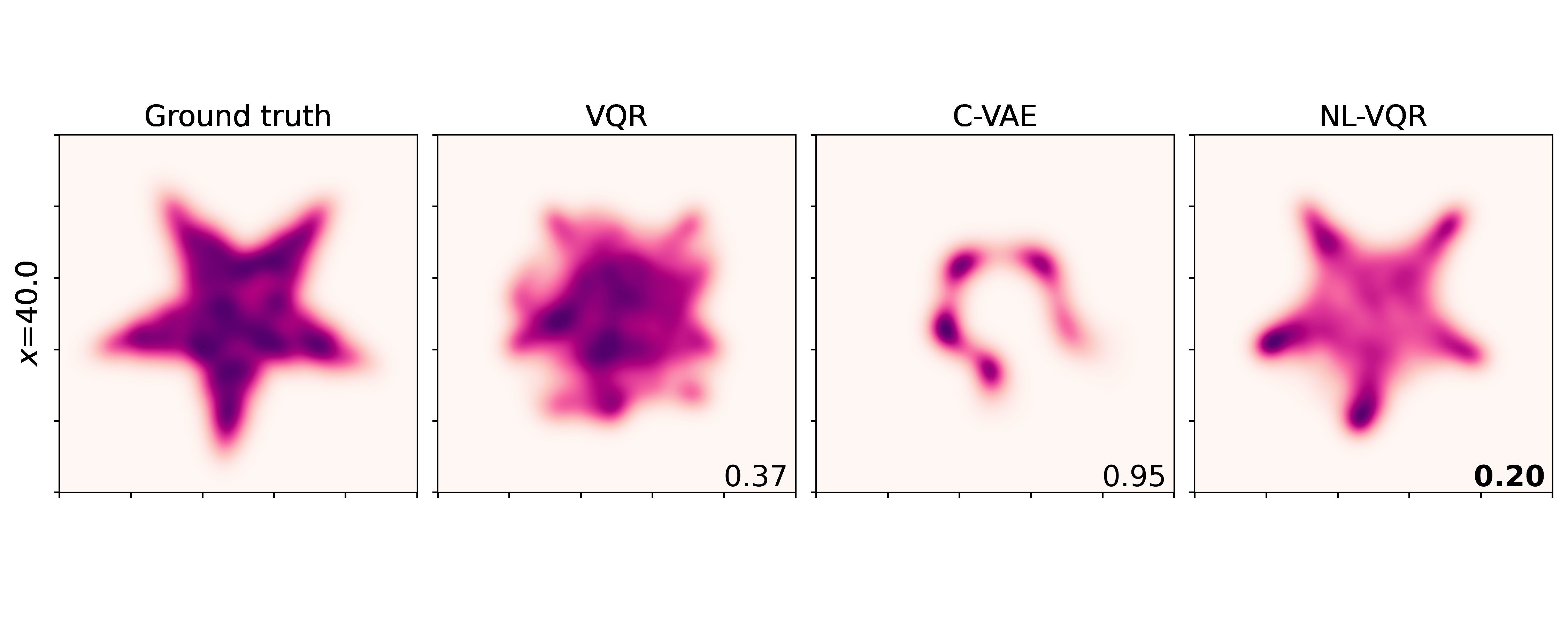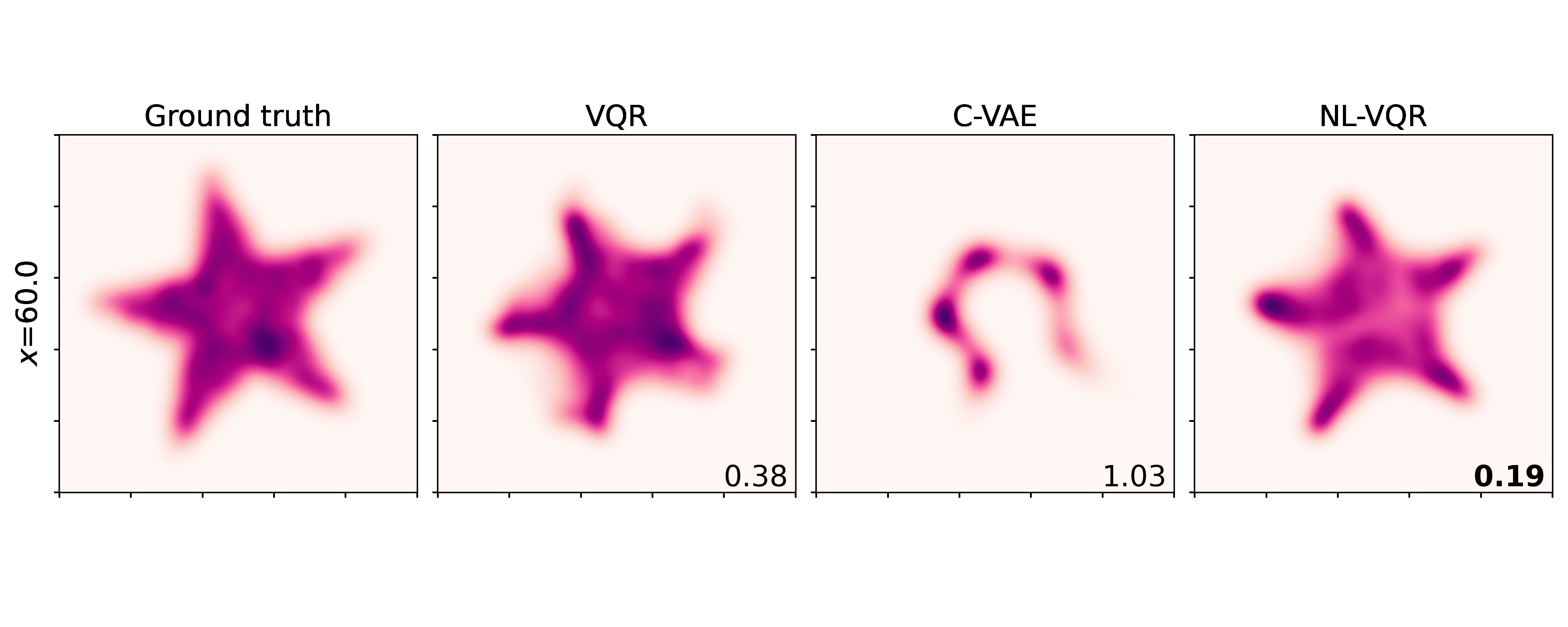
Nonlinear VQR (NL-VQR) outperformes linear VQR and Conditional VAE (C-VAE)[^Feldman2021] on challenging distribution estimation tasks. The metric shown is KDE-L1 distribution distance (lower is better). Comparisons on two synthetic datasets are shown belows.
Conditional banana: In this dataset both the mean of the distribution and its shape change as a nonlinear function of the covariates $\text{X}$.
Rotating stars: Features a nonlinear relationship between the covariates and the quantile function (a rotation matrix), where the conditional mean remains the same for any $\text{X}$, while only the tails (“lowest” and “highest”) quantiles change.
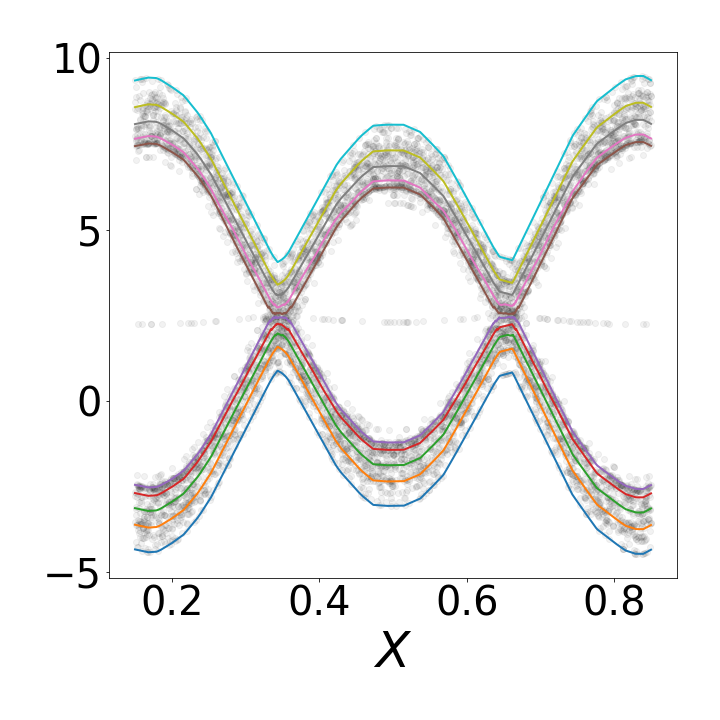
Non-linear Scalar QR
The Nonlinear VQR implementation in this package can be used for performing scalar, i.e. $d=1$, quantile regression. It is very fast since it estimates all $T$ quantile levels simultaneously.
Synthetic glasses: A bi-modal distribution in which the modes' distance depends on $\text{X}$. Note that there are no quantile crossings even when the two modes overlap.
Features
- Vector quantile estimation (VQE): Given samples of a vector-valued random variable $\mathbf{Y}$, estimate its vector quantile function $Q_{\mathbf{Y}}(\boldsymbol{u})$.
- Vector quantile regression (VQR): Given samples from a joint distribution of $(\mathbf{X},\mathbf{Y})$ where $\mathbf{X}$ contains covariates ("feature vector") and $\mathbf{Y}$ is the target variable, estimate the conditional vector quantile function $Q_{\mathbf{Y}|\mathbf{X}}(\boldsymbol{u};\boldsymbol{x})$ (CVQF).
- Vector monotone rearrangement (VMR): an optional refinement procedure for estimated CVQFs which guarantees that the output is a valid quantile function, with no co-monotonicity violations.
- Support for arbitrary learnable non-linear functions of the covariates $g_{\boldsymbol{\theta}}(\boldsymbol{x})$, where the parameters $\boldsymbol{\theta}$ are fitted jointly with the VQR model. Can provide any
pytorchmodel as the learnable transformation. - Sampling: After fitting VQR, new samples can be generated from the conditional distribution. Thus VQR can be used as a generative model which can be fitted on samples, without making any distributional assumptions.
- Calculating quantile $\alpha$-contours: the equivalent of $\alpha$-confidence regions for high-dimensional data.
- Works for any $d\geq 1$. Specifically, for $d=1$, provides an incredibly fast method for performing nonlinear scalar quantile regression which estimates multiple quantiles of the target variable simultaneously.
- Multiple solvers supported as backends. The VQE/VQR API can work with different solver implementations which can provide different benefits and tradeoffs. Easy to integrate new solvers.
- GPU support.
- Coverage and area calculation: measures whether samples are within some $\alpha$-contour of the fitted quantile function, and also the area of these contours.
- Plotting: Basic capabilities for plotting 2d and 3d quantile functions.
Installation
Simply install the vqr package via pip:
pip install vqr
To run the example notebooks, please clone this repo and install the supplied conda environment.
conda env update -f environment.yml -n vqr
conda activate vqr
Usage examples
Below is a minimal usage example for VQR, demonstrating fitting linear VQR, sampling from the conditional distribution, and calculating coverage at a specified $\alpha$.
import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from vqr import VectorQuantileRegressor
from vqr.solvers.dual.regularized_lse import RegularizedDualVQRSolver
N, d, k, T = 5000, 2, 1, 20
N_test = N // 10
seed = 42
alpha = 0.05
# Generate some data (or load from elsewhere).
X, Y = make_regression(
n_samples=N, n_features=k, n_targets=d, noise=0.1, random_state=seed
)
X_train, X_test, Y_train, Y_test = train_test_split(
X, Y, test_size=N_test, shuffle=True, random_state=seed
)
# Create the VQR solver and regressor.
vqr_solver = RegularizedDualVQRSolver(
verbose=True, epsilon=1e-2, num_epochs=1000, lr=0.9
)
vqr = VectorQuantileRegressor(n_levels=T, solver=vqr_solver)
# Fit the model on the data.
vqr.fit(X_train, Y_train)
# Marginal coverage calculation: for each test point, calculate the
# conditional quantiles given x, and check whether the corresponding y is covered
# in the alpha-contour.
cov_test = np.mean(
[vqr.coverage(Y_test[[i]], X_test[[i]], alpha=alpha) for i in range(N_test)]
)
print(f"{cov_test=}")
# Sample from the fitted conditional distribution, given a specific x.
Y_sampled = vqr.sample(n=100, x=X_test[0])
# Calculate conditional coverage given a sample x.
cov_sampled = vqr.coverage(Y_sampled, x=X_test[0], alpha=alpha)
print(f"{cov_sampled=}")
For further examples, please fefer to the example notebooks in the notebooks/ folder of this repo.
References
[^Koenker1978]: Koenker, R. and Bassett Jr, G., 1978. Regression quantiles. Econometrica: journal of the Econometric Society, pp.33-50. [^Carlier2016]: Carlier, G., Chernozhukov, V. and Galichon, A., 2016. Vector quantile regression: an optimal transport approach. The Annals of Statistics, 44(3), pp.1165-1192. [^VQR2022]: Rosenberg, A.A., Vedula, S., Romano, Y. and Bronstein, A.M., 2022. Fast Nonlinear Vector Quantile Regression. arXiv preprint arXiv:2205.14977. [^Feldman2021]: Feldman, S., Bates, S. and Romano, Y., 2021. Calibrated multiple-output quantile regression with representation learning. arXiv preprint arXiv:2110.00816.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file vqr-0.2.0.tar.gz.
File metadata
- Download URL: vqr-0.2.0.tar.gz
- Upload date:
- Size: 96.5 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.9.13
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 1f3a72d74831cf538daf94d1b287e8685c16ccffc32903e8eb116dfb54fb8709 |
|
| MD5 | 884d4216b5dc37e2117e13e023476611 |
|
| BLAKE2b-256 | 4328ce9dfb1f29f0eb82e8da827ec7ec89d81b6d5c2ad8ec273f025fdb9e7e9b |
File details
Details for the file vqr-0.2.0-py2.py3-none-any.whl.
File metadata
- Download URL: vqr-0.2.0-py2.py3-none-any.whl
- Upload date:
- Size: 33.9 kB
- Tags: Python 2, Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.9.13
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 862105f27d8b06bfb64b926a6461b59e84c4dd04ddf98067d3d523fc05d0dd4e |
|
| MD5 | e7570e96626610c499088adae1d07344 |
|
| BLAKE2b-256 | 37f95c3362f9ee676c579ab098a42d49c2c2834921d7cd924bac3cdf2509dfde |