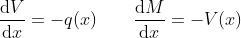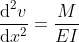A pedagogical package for bending diagrams
Project description
A pedagogical package for beam bending.
SymBeam is a pedagogical software package, written in Python, targeted at Mechanical, Civil and Industrial Engineering students learning the fundamentals of bending of beams, namely, bending diagrams and deflections.
The modular object-oriented-based design of SymBeam combined with the excellent symbolic engine SymPy, on which SymBeam relies heavily, provides a unique computational learning environment for students grasping these concepts for the first time. SymBeam can be exploited to quickly assess the solutions of exercises for a wide variety of bending loadings and supports while allowing to easily modify the parameters of the problem, fostering physical intuition and improving the students' understanding of the phenomena.
Conversely, SymBeam can also be used by teachers to create and validate new problems for classes and exams, facilitating this sometimes cumbersome task.
The following paragraphs provide a detailed description of how to use SymBeam for solving a beam equilibrium problem, together with the extent of its capabilities and also limitations. Check the comprehensive list of SymBeam application examples for a more visual overview.
Try it out
You do not need to be a Python Pro or even know Python at all to use SymBeam in your study. Explore this interactive notebook and enjoy from SymBeam features in your study!
As of February 2021, SymBeam is now part of Centric Engineers online platform. Here you can find a very friendly Graphical User Interface for multiple open-source projects on structural engineering. Check their bending diagrams utility powered by SymBeam!
Installation
Installing from source
Clone this repository into your system
git clone git@github.com:amcc1996/symbeam.git
and install the Python package with pip3, running the following command inside SymBeam root directory, where the setup.py is located
pip3 install .
Alternatively, you can install it directly from PyPI with
pip3 install symbeam
At this point, SymBeam can be imported into your Python scripts and modules the usual Python-way
import symbeam
Theory
SymBeam is based on classical Solid Mechanics and Strength of Materials results to solve the beam equilibirum problem. A simple outline follows in the present section, without entering in any mathematical derivations.
- Reaction computation - SymBeam does not allow for axial loads, currently. Therefore, depending on the support type, one shall need to compute a either a transverse reaction force or a reaction moment. These are computed by solving the algebraic system of linear equations arising from the equilibirum of forces and moments of the structure, accounting simultaneously for point loads and moments and distributed forces.
- Bending diagrams - the shear force and bending moment diagrams are computed by integrating the differential equations of equilibirum of the beam and imposing the boundary conditions in a sequential manner, starting from the initial point at
x0. The expressions obtained at the previous segment are used to set the boundary conditions for the next one.
- Deflection - the slope and deflection of the beam are obtained by integration the elastic curve equation in each segment one and two times, respectively. The geometrical boundary conditions are used to build a system of algebraic equations for the integration constants (twice the number of segments).
Usage
All useful features of SymBeam can be accessed through the beam class. beam objects, this is, concrete instances of the beam class, are initially defined by the starting x-coordinate and the beam length (tacitly assumed to be in the positive x-direction). The beam's supports, material and section properties and loadings are set by calling a specific set of methods on the beam object.
In the following sections, a thorough description of an exemplar application of SymBeam is given. It should be noted beforehand that most (if not all) values characterising the problem can be set either using numerical input (e.g. 100) or a literal expression ('100 * x + 100'). In any case, this input is sympified using SymPy facilities, allowing to handle input of distinct types out-of-the-box. The example to be analysed is illustrated in the following figure (distributed loads on the top side of the beam denote downward forces).

:warning: The
xsymbol is used by SymBeam as the independent variable for the position along the beam. This variable must be used to specify any variation along the length of the beam and for nothing else.
Creating a beam
The fundamental tool for a bending analysis with SymBeam is a beam object, as emphasised above. To create a new beam, import the beam class from the SymBeam package. Then, simply call the beam constructor by passing the length of the beam and, if needed, a starting point (0 by default). For instance, a beam with a length equal to 1 and starting at 0 can be created by
from symbeam import beam
new_beam = beam(1, x0=0)
As claimed before, one can create a beam with both numeric and symbolic input. A list of the distinct alternatives for instantiating a beam follows (the optional initial position x0 is omitted here, for simplicity). Note that these alternatives also apply to any input data that can be given to beam methods, for instance, for specifying supports, loads and properties.
- Numeric input
from symbeam import beam
new_beam = beam(1)
- Numeric input from string
from symbeam import beam
new_beam = beam("1")
- Symbolic input from string
from symbeam import beam
new_beam = beam("L")
- Symbolic input from a symbolic variable created with SymPy
from symbeam import beam
import sympy
L = sympy.symbols("L")
new_beam = beam(L)
- Symbolic input from a symbolic variable provided by SymPy
from symbeam import beam
from sympy.abc import L
new_beam = beam(L)
Setting beam properties: Young modulus and second moment of area
A beam must be associated with some distribution of material properties and section geometry along its length, namely, the Young modulus of the material and the second moment of area of the section. While these are not required for finding the bending diagrams, as these results simply from equilibrium considerations, they are mandatory for computing the deflections of the beam.
In SymBeam, these properties can be set in individual segments along the beam, such that the set of segments for each property must encompass all the beam span and not be overlapping at any region. For example, consider a beam of length L, the Young modulus and second moment of area are set by passing the starting and ending coordinate and the value to the methods set_young() and set_inertia() as follows
from symbeam import beam
from sympy.abc import L, E, I
new_beam = beam(L)
# new_beam.set_young(x_start, x_end, value)
new_beam.set_young(0, L/2, E)
new_beam.set_young(L/2, L, E/10)
# new_beam.set_inertia(x_start, x_end, value)
new_beam.set_inertia(0, L/2, I)
new_beam.set_inertia(L/2, L, I/2)
By default, if the properties are not explicitly set by the user, SymBeam considers constant values E and I along the span of the beam, this is, the property setting methods do not need to be evoked. If any segment is explicitly set, the user must then consistently specify all segments.
:warning: Our beloved symbols E and I: Be careful when specifying symbolic Young modulus and second moment of area via strings, for instance, with "E" and "I". SymPy parses the string in the expression and will interpret "E" as the Euler's number and "I" as the imaginary unit. Prioritise using the variables directly imported from
sympy.abcor create the variables directly withsympy.symbols().
Adding supports
The beam must be connected to the exterior via a given number of supports, which materialise the geometric boundary conditions of the problem. Currently, SymBeam can only solve statically determinate beams, therefore, redundant supports cannot be handled. Supports can be added to the beam by specifying the coordinate and the type of support. Exemplarily, this is accomplished by calling the method add_support()
# new_beam.add_support(x_coord, type)
new_beam.add_support(0, 'fixed')
new_beam.add_support(L, 'roller')
new_beam.add_support(3*L/4, 'hinge')
The types of support available in SymBeam are
roller: a roller, fixed in the transverse direction and allows rotations in the bending planepin: a pinned support, fixed in the axial and transverse directions and allows rotations in the bending planefixed: a fixed/clamped support, all degrees of freedom are constrained (no displacements and no rotation)hinge: allows distinct rotations on the left and right of the point, but does not fix the beam in any direction
Adding loads
The applied external loads are the missing item for completely defining the beam bending problem. These can be point-type, namely, transverse point loads/forces and moments, and segment-type loads, this is, transverse forces distributed along the span of the beam.
Point loads and moments are incorporated by calling the add_point_load() and add_point_moment() methods, which receive the coordinate of the point and the value of the load. Distributed loads are applied by calling the add_distributed_load() method, which takes the starting and ending point of the distributed load and the associated expression.
# new_beam.add_point_load(x_coord, magnitude)
# new_beam.add_point_moment(x_coord, magnitude)
# new_beam.add_distributed_load(x_start, x_end, expression)
new_beam.add_point_load(3*L/4, -P)
new_beam.add_point_moment(L, M)
new_beam.add_distributed_load(0, L/2, -q * x)
Solving the problem
After specifying the beam properties, supports and loads, the problem can be solved by calling the method solve(). The program will proceed as follows
- check if the input data is consistent
- define the individual beam segments, such that each one is associated with a continuous function of the Young modulus, second moment of area and distributed load: in sum, this subdivision must guarantee that the shear force and bending moment diagrams are continuous in each segment and piecewise continuous along the span of the beam
- solve for the reaction forces and moments of the supports (equilibrium equations)
- solve for the internal loads (integrate the differential equations for beam equilibrium)
- solve for the deflections (integrate the elastic curve equation)
- output the results (can be suppressed if the optional argument
output=False): identified segments, exterior reactions, shear force, bending moment, slope and deflection for each beam segment. For the current example, the output shall be as follows.
Beam points
===================================================================================
Coordinate Type Load Moment
-----------------------------------------------------------------------------------
0 Fixed 0 0
L/2 Continuity point 0 0
3*L/4 Hinge -P 0
L Roller 0 M
===================================================================================
Beam segments
===================================================================================
Span Young modulus Inertia Distributed load
-----------------------------------------------------------------------------------
[ 0 - L/2 ] E I -q*x
[ L/2 - 3*L/4 ] E/10 I/2 0
[ 3*L/4 - L ] E/10 I/2 0
===================================================================================
Exterior Reactions
===================================================================================
Point Type Value
-----------------------------------------------------------------------------------
0 Force L**2*q/8 + P + 4*M/L
0 Moment L**3*q/24 + 3*L*P/4 + 3*M
L Force -4*M/L
===================================================================================
Internal Loads
===================================================================================
Span Diagram Expression
-----------------------------------------------------------------------------------
[ 0 - L/2 ] V(x) -L**2*q/8 - P + q*x**2/2 - 4*M/L
[ 0 - L/2 ] M(x) -L**3*q/24 - 3*L*P/4 - 3*M - q*x**3/6 + x*(L**3*q + 8*L*P + 32*M)/(8*L)
-----------------------------------------------------------------------------------
[ L/2 - 3*L/4 ] V(x) -P - 4*M/L
[ L/2 - 3*L/4 ] M(x) -3*L*P/4 - 3*M + x*(P + 4*M/L)
-----------------------------------------------------------------------------------
[ 3*L/4 - L ] V(x) -4*M/L
[ 3*L/4 - L ] M(x) -3*M + 4*M*x/L
===================================================================================
Rotation and deflection
===================================================================================
Span Variable Expression
-----------------------------------------------------------------------------------
[ 0 - L/2 ] v(x) -q*x**5/(120*E*I) + x**2*(-L**3*q - 18*L*P - 72*M)/(48*E*I) + x**3*(L**3*q + 8*L*P + 32*M)/(48*E*I*L)
[ 0 - L/2 ] dv/dx(x) -q*x**4/(24*E*I) + x*(-L**3*q - 18*L*P - 72*M)/(24*E*I) + x**2*(L**3*q + 8*L*P + 32*M)/(16*E*I*L)
-----------------------------------------------------------------------------------
[ L/2 - 3*L/4 ] v(x) L**2*(L**3*q - 950*L*P - 3800*M)/(960*E*I) + L*x*(-L**3*q + 608*L*P + 2432*M)/(128*E*I) + x**2*(-15*L*P - 60*M)/(2*E*I) + x**3*(10*L*P + 40*M)/(3*E*I*L)
[ L/2 - 3*L/4 ] dv/dx(x) L*(-L**3*q + 608*L*P + 2432*M)/(128*E*I) + x*(-15*L*P - 60*M)/(E*I) + x**2*(10*L*P + 40*M)/(E*I*L)
-----------------------------------------------------------------------------------
[ 3*L/4 - L ] v(x) -L**2*(37*L**3*q + 1840*L*P + 16960*M)/(1920*E*I) + L*x*(37*L**3*q + 1840*L*P + 48960*M)/(1920*E*I) - 30*M*x**2/(E*I) + 40*M*x**3/(3*E*I*L)
[ 3*L/4 - L ] dv/dx(x) L*(37*L**3*q + 1840*L*P + 48960*M)/(1920*E*I) - 60*M*x/(E*I) + 40*M*x**2/(E*I*L)
===================================================================================
:warning: Don't be scared by the output: The chosen example encompasses several features of SymBeam, therefore, the analytical expressions tend to grow in size very rapidly, especially the deflection.
Plotting the results
The results can be plotted with matplotlib by calling the method plot on the beam object. The produced figure contains
- a schematic representation of the problem
- the shear force diagram
- the bending moment diagram
- the deformed shape of the beam.
At this stage, to be able to plot the expressions, all the parameters of the problem must be substituted by numerical values, with the natural exception of the x variable, since this is the independent variable. This is can be accomplished by passing the optional argument subs to the plot method. This must be a dictionary whose keys are the string representations of the variables and the values are the effective numerical values.
Adopting the substitutions L=2, P=1000, q=5000 and M=1000, SymBeam outputs the figure below.

:warning: Do not forget to save the figures with
savefig()method frommatplotlib.pyplot.figure. In fact, you can also simply print the figure to the screen withshow()frommatplotlib.pyplot, but be aware that this might unformat the layout slightly, depending on the characteristics of your system.
Final script
Here you can find the complete script discussed on the previous sections.
from symbeam import beam
from sympy.abc import L, E, I, P, M, q, x
import matplotlib.pyplot as plt
new_beam = beam(L)
# new_beam.set_young(x_start, x_end, value)
new_beam.set_young(0, L/2, E)
new_beam.set_young(L/2, L, E/10)
# new_beam.set_inertia(x_start, x_end, value)
new_beam.set_inertia(0, L/2, I)
new_beam.set_inertia(L/2, L, I/2)
# new_beam.add_support(x_coord, type)
new_beam.add_support(0, 'fixed')
new_beam.add_support(L, 'roller')
new_beam.add_support(3*L/4, 'hinge')
# new_beam.add_point_load(x_coord, magnitude)
# new_beam.add_point_moment(x_coord, magnitude)
# new_beam.add_distributed_load(x_start, x_end, expression)
new_beam.add_point_load(3*L/4, -P)
new_beam.add_point_moment(L, M)
new_beam.add_distributed_load(0, L/2, -q * x)
new_beam.solve()
new_beam.plot(subs={'P':1000, 'q':5000, 'L':2, 'M':1000})
plt.savefig("beam.pdf")
Adding springs
As of version 2.1.0, SymBeam can include linear and rotational springs in the analysis. Including springs modifies significantly the way calculations are carried out. Without springs, the problem can be solver sequentially since there is no bi-directional coupling between each phase:
- Solve for reactions;
- Solve for internal loads (which depends on the reactions);
- Solve for deflecetions (which depends on the internal loads). With springs, however, reactions are coupled with the deflection calculation, thus the problem needs to be solved in a monolithic way for all unknowns all at once.
To add springs to your beam, you just have to add one of these lines to your script.
new_beam.add_transverse_spring(x_coord, k_v) # k_v in N/m
new_beam.add_rotational_spring(x_coord, k_theta) # k_theta in Nm/rad
Notice that transverse_springrefers to linear springs transverse to the beam and rotational_spring refers to angular/rotation springs. Currently, only a linear spring model has been implemented, where the force is proportional to the deflection and rotation at point x_coord and the coefficients are the sitffness values k_v and k_theta.
Here follows an example with different combinations of springs. For more examples, new problems were added to the examples folder, particularly examples 18 to 21.
import matplotlib.pyplot as plt
from sympy.abc import x
from symbeam import beam
L = 1 # Length of the beam in m
E = 210e3 # Young's modulus in Pa
I = 1e-6 # Moment of inertia in m^4
P = 1000 # Point load in N
M = 200 # Point moment in Nm
q = 2000 # Distributed load in N/m
kv = 1e3 # Transverse spring stiffness in N/m
ktheta = 1e3 # Rotational spring stiffness in Nm/rad
new_beam = beam(L)
# new_beam.set_young(x_start, x_end, value)
new_beam.set_young(0, L, E)
# new_beam.set_inertia(x_start, x_end, value)
new_beam.set_inertia(0, L, I)
# new_beam.add_support(x_coord, type)
new_beam.add_support(0, "pin")
new_beam.add_support(L, "roller")
# new_beam.add_point_load(x_coord, magnitude)
# new_beam.add_point_moment(x_coord, magnitude)
# new_beam.add_distributed_load(x_start, x_end, expression)
new_beam.add_point_load(L / 3, -P)
new_beam.add_point_moment(2 * L / 3, M)
new_beam.add_distributed_load(0, L, -q * x / L)
# new_beam.add_transverse_spring(x_coord, k_v)
# new_beam.add_rotational_spring(x_coord, k_theta)
new_beam.add_rotational_spring(0, ktheta)
new_beam.add_transverse_spring(L / 2, kv)
new_beam.add_rotational_spring(L / 4, ktheta)
new_beam.add_transverse_spring(3 * L / 4, kv)
new_beam.add_rotational_spring(3 * L / 4, ktheta)
new_beam.add_rotational_spring(L, ktheta)
new_beam.solve()
new_beam.plot()
plt.savefig("beam_with_springs.pdf")
Running this script should produce the figure below.

You can place prings anywhere along the beam, with the following exceptions:
- Rotational springs on hinges and fixed supports are not accepted.
- Transverse springs on rollers, pins and fixed supports are not accepted.
Notice, however, that you can add rotational springs to pins and rollers to enforce full constraints on the transverse displacement, but still allow for some rotational flexibility.
In the limit of infinite spring stiffness, the springs mimic rigid supports.
Considering for example a cantilever beam fixed at x=0 and subjected to a for P at x=L, which is setup ins SymBeam as
new_beam = beam(L)
new_beam.set_young(0, L, E)
new_beam.set_inertia(0, L, I)
new_beam.add_point_load(L, P)
new_beam.add_support(0, 'fixed')
The fixed support can be replaced by two springs, whose stiffness is parameterised by a, as
new_beam = beam(L)
new_beam.set_young(0, L, E)
new_beam.set_inertia(0, L, I)
new_beam.add_point_load(L, P)
new_beam.add_transverse_spring(0, a * E * I / L**3)
new_beam.add_rotational_spring(0, a * E * I / L)
If we compute the analytical solution with and without the springs for different values of a we get the figure below (check this script). The delfection with the spring converges to the the rigid support solution as the stiffness grows to infinity.

:warning: Adding springs to your beam can render the symbolic solution to your problem extremely complicated. SymBeam supports symbolic springs, as shown in example 17. However, you should prepare your self for true symbolic monstruosities if your beam is complex and has springs.
Running the tests
SymBeam tests can by run with pytest and the image comparison plugin pytest-mpl, so start by installing the framework
pip3 install pytest pytest-mpl
pip3 install pytest-cov # optional, to generate coverage reports
and launch the testing utility from SymBeam root directory
make tests
SymBeam uses pytest-mpl for comparing the bending plots between versions. By evoking make tests, pytest will be called with the appropriate command-line tool and directory settings. The reference images are stored in tests/baseline. If there image comparison fails, the baseline image is written to tests/results, together with the (failing) image produced my the current version and the respective difference.
The coverage reports can be generated with
make coverage
which will run the test and create the coverage information in htmlcov.
License
Copyright 2020, António Carneiro
SymBeam is free and open-source software and is published under MIT License.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file symbeam-2.1.1.tar.gz.
File metadata
- Download URL: symbeam-2.1.1.tar.gz
- Upload date:
- Size: 181.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: uv/0.9.18 {"installer":{"name":"uv","version":"0.9.18","subcommand":["publish"]},"python":null,"implementation":{"name":null,"version":null},"distro":{"name":"Debian GNU/Linux","version":"13","id":"trixie","libc":null},"system":{"name":null,"release":null},"cpu":null,"openssl_version":null,"setuptools_version":null,"rustc_version":null,"ci":null}
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
e13a52d29067552a91e16109696c21e787e8ef2b6aa327502a47da1d76ae0956
|
|
| MD5 |
2cd70111bf75e937c0025d312964d420
|
|
| BLAKE2b-256 |
43b929fd7c2d0d59c9e4cb49a90439406431932c62f02cefe5c39cb42c14a048
|
File details
Details for the file symbeam-2.1.1-py3-none-any.whl.
File metadata
- Download URL: symbeam-2.1.1-py3-none-any.whl
- Upload date:
- Size: 33.0 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: uv/0.9.18 {"installer":{"name":"uv","version":"0.9.18","subcommand":["publish"]},"python":null,"implementation":{"name":null,"version":null},"distro":{"name":"Debian GNU/Linux","version":"13","id":"trixie","libc":null},"system":{"name":null,"release":null},"cpu":null,"openssl_version":null,"setuptools_version":null,"rustc_version":null,"ci":null}
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
c7b869e5ff7052a9420edc6d8f6ef56e54caaaeecf9536e9b05259f9be701e26
|
|
| MD5 |
217343eca2d00a628eb06d0e3792f118
|
|
| BLAKE2b-256 |
7f7e05c5bd32777ba6ea3741c3eaf307e642d85d98d9d7216b0af3f71ba25e19
|