Compute discrete Ricci curvatures and Ricci flow on NetworkX graphs.
Project description
GraphRicciCurvature
A Python library to compute Discrete Ricci curvature, Ricci flow, and Ricci community on NetworkX graph.
This work computes the Ollivier-Ricci Curvature[Ni], Ollivier-Ricci Flow[Ni2,Ni3], Forman-Ricci Curvature(or Forman curvature)[Sreejith, Samal], and Ricci community[Ni3] detected by Ollivier-Ricci flow metric.
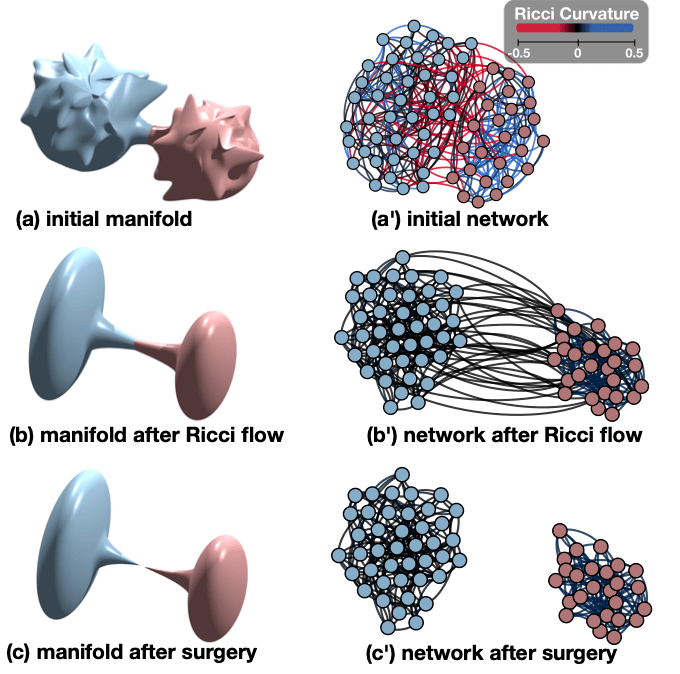
Curvature is a geometric property to describe the local shape of an object. If we draw two parallel paths on a surface with positive curvature like a sphere, these two paths move closer to each other while for a negatively curved surface like a saddle, these two paths tend to be apart. Currently there are multiple ways to discretize curvature on graph, in this library, we include two of the most frequently used discrete Ricci curvature: Ollivier-Ricci curvature which is based on optimal transportation theory and Forman-Ricci curvature which is base on CW complexes.
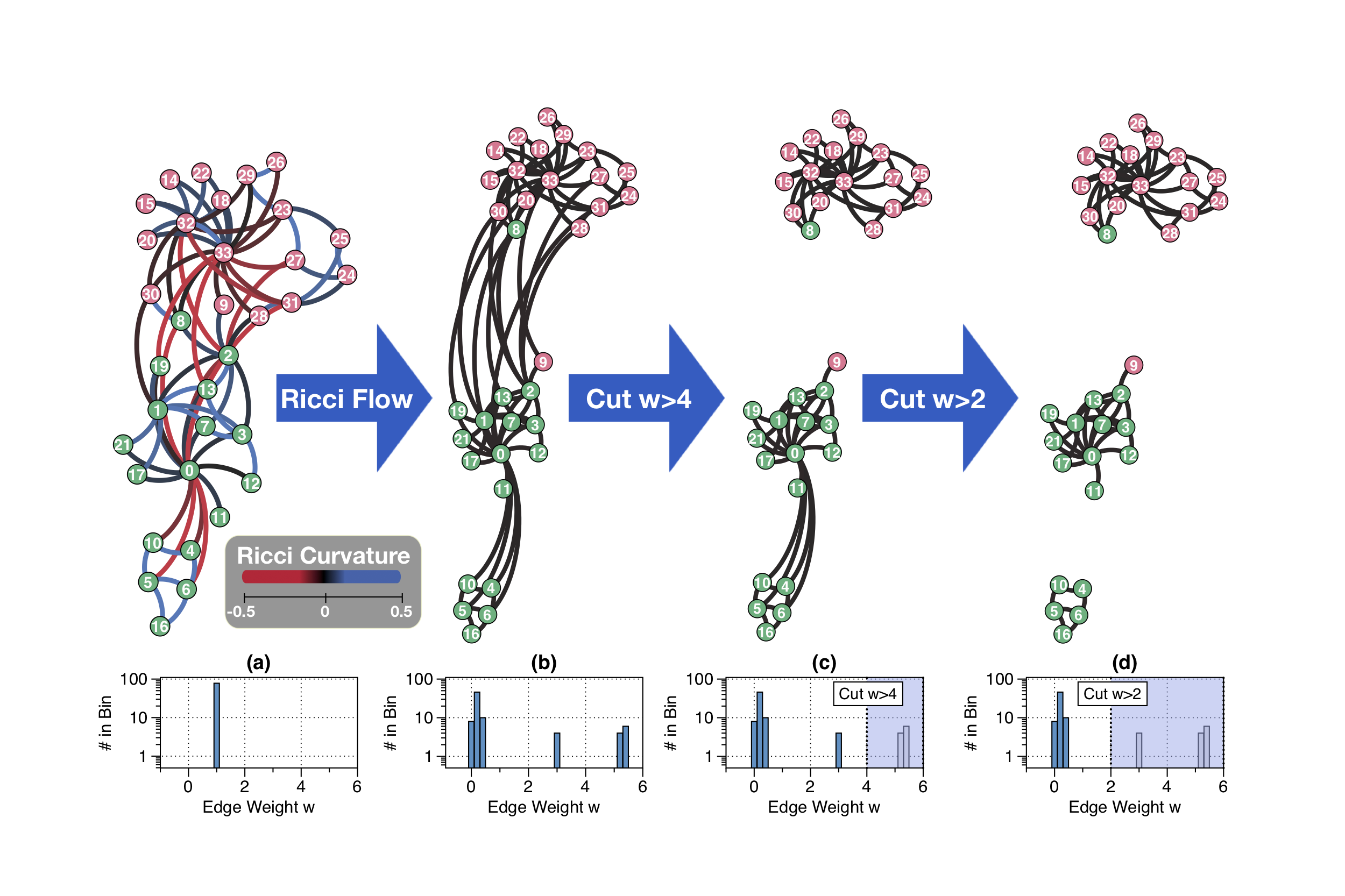
In [Ni], edge Ricci curvature is observed to play an important role in the graph structure. An edge with positive curvature represents an edge within a cluster, while a negatively curved edge tent to be a bridge within clusters. Also, negatively curved edges are highly related to graph connectivity, with negatively curved edges removed from a connected graph, the graph soon become disconnected.
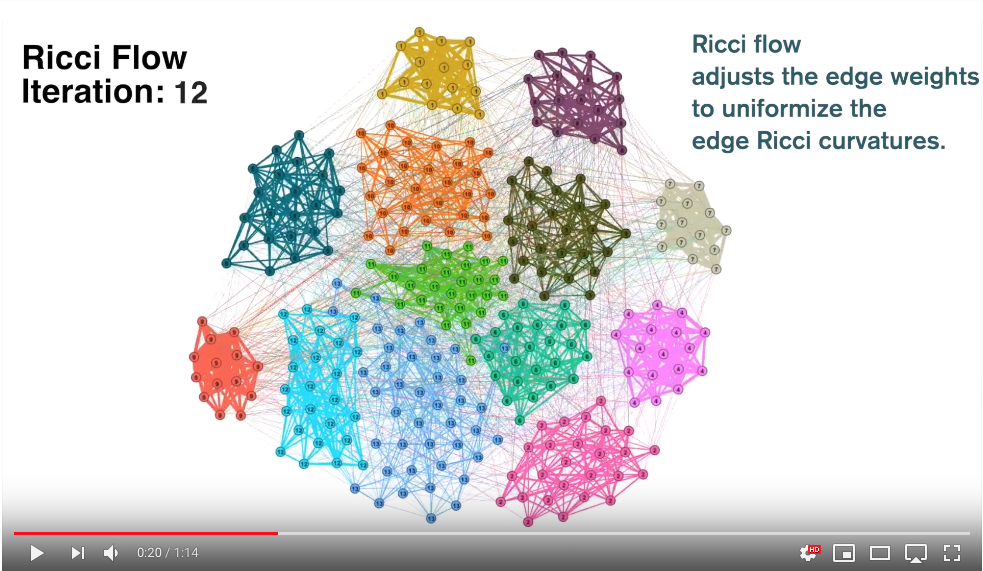
Ricci flow is a process to uniformized the edge Ricci curvature of the graph. For a given graph, the Ricci flow gives a "Ricci flow metric" on each edge as edge weights, such that under these edge weights, the Ricci curvature of the graph is mostly equal everywhere. In [Ni3], this "Ricci flow metric" is shown to be able to detect communities.
Both Ricci curvature and Ricci flow metric can act as a graph fingerprint for graph classification. The different graph gives different edge Ricci curvature distributions and different Ricci flow metric.
Video demonstration of Ricci flow for community detection:
Package Requirement
- NetworkX >= 2.0 (Based Graph library)
- NetworKit >= 6.1 (Shortest path algorithm)
- NumPy (POT support)
- POT (For optimal transportation distance)
- python-louvain (For faster modularity computation)
Installation
Installing via pip
pip3 install [--user] GraphRicciCurvature
- From version 0.4.0, NetworKit is required to compute shortest path for density distribution. If the installation of NetworKit failed, please refer to NetworKit' Installation instructions.
Upgrading via pip
To run with the latest code for the best performance, upgrade GraphRicciCurvature to the latest version with pip:
pip3 install [--user] --upgrade GraphRicciCurvature
Getting Started
- Check the jupyter notebook tutorial on nbviewer or github for a walk through for the basic usage of Ricci curvature, Ricci flow, and Ricci flow for community detection.
- Or you can run it in directly on binder (no account required) or Google colab (Faster but Google account required).
- Check the Documentations.
- Try out sample graphs with precomputed Ricci curvature/flow.
Simple Example
import networkx as nx
from GraphRicciCurvature.OllivierRicci import OllivierRicci
from GraphRicciCurvature.FormanRicci import FormanRicci
print("\n- Import an example NetworkX karate club graph")
G = nx.karate_club_graph()
print("\n===== Compute the Ollivier-Ricci curvature of the given graph G =====")
# compute the Ollivier-Ricci curvature of the given graph G
orc = OllivierRicci(G, alpha=0.5, verbose="INFO")
orc.compute_ricci_curvature()
print("Karate Club Graph: The Ollivier-Ricci curvature of edge (0,1) is %f" % orc.G[0][1]["ricciCurvature"])
print("\n===== Compute the Forman-Ricci curvature of the given graph G =====")
frc = FormanRicci(G)
frc.compute_ricci_curvature()
print("Karate Club Graph: The Forman-Ricci curvature of edge (0,1) is %f" % frc.G[0][1]["formanCurvature"])
# -----------------------------------
print("\n===== Compute Ricci flow metric - Optimal Transportation Distance =====")
G = nx.karate_club_graph()
orc_OTD = OllivierRicci(G, alpha=0.5, method="OTD", verbose="INFO")
orc_OTD.compute_ricci_flow(iterations=10)
print("\n===== Compute Ricci community - by Ricci flow =====")
clustering = orc_OTD.ricci_community()
More example in example.py.
Related Works
- Curvature Graph Network (ICLR2020) openreview, code
Reference
[Ni]: Ni, C.-C., Lin, Y.-Y., Gao, J., Gu, X., and Saucan, E. "Ricci curvature of the Internet topology" (Vol. 26, pp. 2758–2766). Presented at the 2015 IEEE Conference on Computer Communications (INFOCOM), IEEE. arXiv
[Ni2]: Ni, C.-C., Lin, Y.-Y., Gao, J., and Gu, X. "Network Alignment by Discrete Ollivier-Ricci Flow", Graph Drawing 2018, arXiv
[Ni3]: Ni, C.-C., Lin, Y.-Y., Luo, F. and Gao, J. "Community Detection on Networks with Ricci Flow", Scientific Reports 9, 9984 (2019), arXiv
[Sreejith]: Sreejith, R. P., Karthikeyan Mohanraj, Jürgen Jost, Emil Saucan, and Areejit Samal. "Forman Curvature for Complex Networks." Journal of Statistical Mechanics: Theory and Experiment 2016 (6). IOP Publishing: 063206. arxiv
[Samal]: Samal, A., Sreejith, R.P., Gu, J. et al. "Comparative analysis of two discretizations of Ricci curvature for complex networks." Scientific Report 8, 8650 (2018). arXiv
Contact
Please contact Chien-Chun Ni.
Cite
If you use this code in your research, please considering cite our paper:
@article{ni2019community,
title={Community detection on networks with ricci flow},
author={Ni, Chien-Chun and Lin, Yu-Yao and Luo, Feng and Gao, Jie},
journal={Scientific reports},
volume={9},
number={1},
pages={1--12},
year={2019},
publisher={Nature Publishing Group}
}
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file GraphRicciCurvature-0.5.3.2.tar.gz.
File metadata
- Download URL: GraphRicciCurvature-0.5.3.2.tar.gz
- Upload date:
- Size: 20.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.1.1 CPython/3.11.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
59822f9faddd4f60958bb63549c36eeadc1733d9e2a670d83b5c21470bc00547
|
|
| MD5 |
c3eb997338e926432f63fc633c1b0515
|
|
| BLAKE2b-256 |
c1751ef5604bd816547ae009b2266bec94a36975951440b5f3c412c25731a5b0
|
File details
Details for the file GraphRicciCurvature-0.5.3.2-py3-none-any.whl.
File metadata
- Download URL: GraphRicciCurvature-0.5.3.2-py3-none-any.whl
- Upload date:
- Size: 23.2 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.1.1 CPython/3.11.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a3488572b326931e8a1a11e9cbb513f3f72e1884178d24430ab51ec5ac6810b4
|
|
| MD5 |
bc158f7de0ddf5faa1c2ef2f6a0b68d9
|
|
| BLAKE2b-256 |
00b0ed20266434eb5f354b08d77031a121bf67a234a26bbf9f5d887089da598d
|