An implementation of KD trees
Project description
KD-tree-implementation
An implementation of kd-search trees with functions to find the nearest neighbor, an operation that would take a long time using linear search on large datasets. That is where kd-search trees come in, since they can exclude a larger part of the dataset at once.
This project was created as a final project for the course CS110/Computation: Solving Problems with algorithms.
Installation guide
Open the Command center and paste the following
pip install Katjas-kd-tree
How to run
After installing the package import it by typing
import kd_tree as kd
You are now able to use the following functions
kd.build_tree(dict)
# this will build a kd-tree from a given dictionary of format key:[values]
kd.distance(lsta,lstb)
# returns the distance between two points a and b with coordinates given by lsta and lstb
kd.find_approx_nearest(tree,value)
# returns the approximate nearest neighbor for a given value
kd.find_exact_nearest(tree,value)
# returns the exact nearest element of the tree to the value
Example use case
To find the closest color in a dataset of named colors in the LAB (or CIELAB) color space. This color space works similar to RBG colors, but is design to let make colors that look similar to huymans be closer to each other in the color space. The first dimesnions is a spectrum from light to dark, the other two describe the green-red and blue-yellow value going from negative to positive value. More on LAB colors: https://en.wikipedia.org/wiki/CIELAB_color_space
We cannot use our usual quick-search methods or binary search-trees, since the data has more than 1 dimension and cannot simply be ordered. Therefore, we can create a tree with 3 dimensions, where every new level is split along a new dimension, iterating through all of them as often as needed. This allows us to very quickly get an approximation of the nearest neighbor and with slightly more effort find the exact nearest neighbor quicker than with a linear search.
# importing a dataset of paint colors and their position in the LAB colorspace
with open ("paintcolors.json") as json_file:
paintcolors=json.load(json_file)
# creating a tree out of the paintcolors
painttree=kd.build_tree(paintcolors)
# finding the approximate and exact nearest color to [0,0,0]
print((kd.distance(kd.find_approx_nearest(painttree,[0,0,0]).value,[0,0,0]),
kd.find_approx_nearest(painttree,[0,0,0]).name,
kd.find_approx_nearest(painttree,[0,0,0]).value))
print(kd.find_exact_nearest(painttree,[0,0,0]))
This will return the approximate and exact nearest color to [0,0,0]
(0.23327147726897515, 'UniversalBlack', [0.233007, 0.010686, -0.0030215])
(0.22615200000001437, 'TwilightZone', [0.226152, 5.54817e-08, 5.84874e-08])
The resulting kd-tree looks like this (nodes not above each other for clarity)
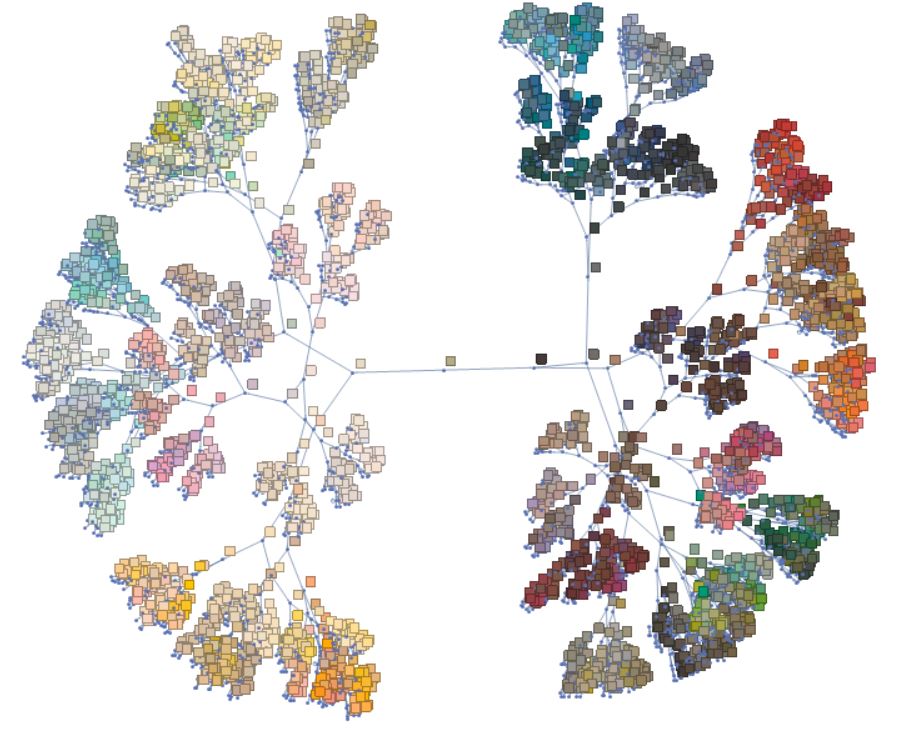
If you would like to run this code for yourself, please download the data from https://github.com/katjadellalibera/KD-tree-implementation/blob/master/paintcolors.json and the code from https://github.com/katjadellalibera/KD-tree-implementation/blob/master/example.py
Background
Time-Complexity:
A linear search runs with O(n) complexity, since it has to check every value. find_approx_nearest runs with $O(\log(n))$ complexity on average, because it just has to go down a binary tree with a depth of $\log_2(n)$. In the worst case we have a oddly shaped tree like one with only two nodes, where the worst-case runtime could be $O(n)$, because every node is visited. The find_exact_nearest function will exclude less of the tree at a time, but still run in $O(\log(n))$, just with a higher constant factor.
Space-Complexity:
Storing the data points as nodes rather than in a dictionary or array will still take $O(n)$ space complexity. There may be a slightly higher constant term k, accounting for the split-dimension d and pointers to the left an right child, but the total complexity is $O(n)$
Dependencies
The implementation depends on a the pre-installed packages random, math and json as well as the numpy package.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file Katjas_kd_tree-0.0.4.tar.gz.
File metadata
- Download URL: Katjas_kd_tree-0.0.4.tar.gz
- Upload date:
- Size: 4.3 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.12.1 pkginfo/1.4.2 requests/2.21.0 setuptools/40.6.3 requests-toolbelt/0.8.0 tqdm/4.28.1 CPython/3.7.1
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
aa2bae4d9836047f9f48091e736436ee1c6a0490f3119cc2d226d9418e85667c
|
|
| MD5 |
ef4cf035862425ce37773b431de3229c
|
|
| BLAKE2b-256 |
a3de86e7366bd9da33d59ff90f1084513aa801e7348b46ce890d5fa21d1701c6
|
File details
Details for the file Katjas_kd_tree-0.0.4-py3-none-any.whl.
File metadata
- Download URL: Katjas_kd_tree-0.0.4-py3-none-any.whl
- Upload date:
- Size: 5.3 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.12.1 pkginfo/1.4.2 requests/2.21.0 setuptools/40.6.3 requests-toolbelt/0.8.0 tqdm/4.28.1 CPython/3.7.1
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
56ddf2415243d9c2b2f5be18fd7a0f7c0c9ca1ffbe91549e555f38ec605c0865
|
|
| MD5 |
a949f926c87ca5219d40e4b0a88a1f48
|
|
| BLAKE2b-256 |
d98aeeae952ded0441402ae953a48f4a4f51695a2b0ee0baa1e7be62115003d3
|










