Solves automatic numerical differentiation problems in one or more variables.
Project description
Numdifftools
Numdifftools is a suite of tools written in _Python to solve automatic numerical differentiation problems in one or more variables. Finite differences are used in an adaptive manner, coupled with a Richardson extrapolation methodology to provide a maximally accurate result. The user can configure many options like; changing the order of the method or the extrapolation, even allowing the user to specify whether complex-step, central, forward or backward differences are used.
The methods provided are:
Derivative: Compute the derivatives of order 1 through 10 on any scalar function.
directionaldiff: Compute directional derivative of a function of n variables
Gradient: Compute the gradient vector of a scalar function of one or more variables.
Jacobian: Compute the Jacobian matrix of a vector valued function of one or more variables.
Hessian: Compute the Hessian matrix of all 2nd partial derivatives of a scalar function of one or more variables.
Hessdiag: Compute only the diagonal elements of the Hessian matrix
All of these methods also produce error estimates on the result.
Numdifftools also provide an easy to use interface to derivatives calculated with in _AlgoPy. Algopy stands for Algorithmic Differentiation in Python. The purpose of AlgoPy is the evaluation of higher-order derivatives in the forward and reverse mode of Algorithmic Differentiation (AD) of functions that are implemented as Python programs.
Getting Started
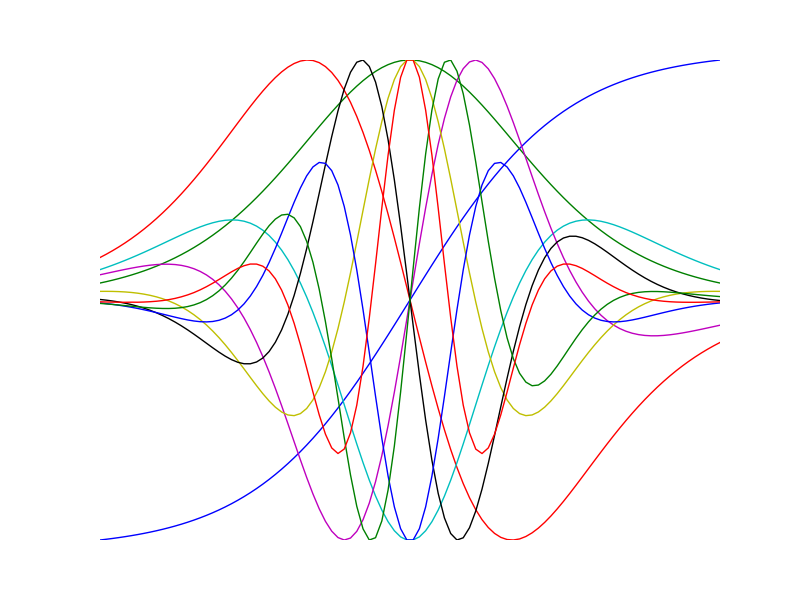
Visualize high order derivatives of the tanh function
>>> import numpy as np >>> import numdifftools as nd >>> import matplotlib.pyplot as plt >>> x = np.linspace(-2, 2, 100) >>> for i in range(10): ... df = nd.Derivative(np.tanh, n=i) ... y = df(x) ... h = plt.plot(x, y/np.abs(y).max())>>> plt.show()
Compute 1’st and 2’nd derivative of exp(x), at x == 1:
>>> fd = nd.Derivative(np.exp) # 1'st derivative >>> fdd = nd.Derivative(np.exp, n=2) # 2'nd derivative >>> np.allclose(fd(1), 2.7182818284590424) True >>> np.allclose(fdd(1), 2.7182818284590424) True
Nonlinear least squares:
>>> xdata = np.reshape(np.arange(0,1,0.1),(-1,1)) >>> ydata = 1+2*np.exp(0.75*xdata) >>> fun = lambda c: (c[0]+c[1]*np.exp(c[2]*xdata) - ydata)**2 >>> Jfun = nd.Jacobian(fun) >>> np.allclose(np.abs(Jfun([1,2,0.75])), 0) # should be numerically zero True
Compute gradient of sum(x**2):
>>> fun = lambda x: np.sum(x**2) >>> dfun = nd.Gradient(fun) >>> dfun([1,2,3]) array([ 2., 4., 6.])
Compute the same with the easy to use interface to AlgoPy:
>>> import numdifftools.nd_algopy as nda >>> import numpy as np >>> fd = nda.Derivative(np.exp) # 1'st derivative >>> fdd = nda.Derivative(np.exp, n=2) # 2'nd derivative >>> np.allclose(fd(1), 2.7182818284590424) True >>> np.allclose(fdd(1), 2.7182818284590424) True
Nonlinear least squares:
>>> xdata = np.reshape(np.arange(0,1,0.1),(-1,1)) >>> ydata = 1+2*np.exp(0.75*xdata) >>> fun = lambda c: (c[0]+c[1]*np.exp(c[2]*xdata) - ydata)**2 >>> Jfun = nda.Jacobian(fun, method='reverse') >>> np.allclose(np.abs(Jfun([1,2,0.75])), 0) # should be numerically zero True
Compute gradient of sum(x**2):
>>> fun = lambda x: np.sum(x**2) >>> dfun = nda.Gradient(fun) >>> dfun([1,2,3]) array([ 2., 4., 6.])
See also
scipy.misc.derivative
Documentation and code
Numdifftools works on Python 2.7+ and Python 3.0+.
Official releases available at: http://pypi.python.org/pypi/numdifftools
Official documentation available at: http://numdifftools.readthedocs.io/en/latest/
Bleeding edge: https://github.com/pbrod/numdifftools.
Installation
If you have pip installed, then simply type:
$ pip install numdifftools
to get the lastest stable version. Using pip also has the advantage that all requirements are automatically installed.
Unit tests
To test if the toolbox is working paste the following in an interactive python session:
import numdifftools as nd nd.test(coverage=True, doctests=True)
Acknowledgement
The numdifftools package for Python was written by Per A. Brodtkorb based on the adaptive numerical differentiation toolbox written in Matlab by John D’Errico [DErrico2006].
Numdifftools has as of version 0.9 been extended with some of the functionality found in the statsmodels.tools.numdiff module written by Josef Perktold [Perktold2014].
References
D’Errico, J. R. (2006), Adaptive Robust Numerical Differentiation http://www.mathworks.com/matlabcentral/fileexchange/13490-adaptive-robust-numerical-differentiation
Perktold, J (2014), numdiff package http://statsmodels.sourceforge.net/0.6.0/_modules/statsmodels/tools/numdiff.html
Gregory Lantoine (2010), A methodology for robust optimization of low-thrust trajectories in multi-body environments, Phd thesis, Georgia Institute of Technology
Gregory Lantoine, R.P. Russell, and T. Dargent (2012) Using multicomplex variables for automatic computation of high-order derivatives, ACM Transactions on Mathematical Software, Vol. 38, No. 3, Article 16, April 2012, 21 pages, http://doi.acm.org/10.1145/2168773.2168774
M.E. Luna-Elizarraras, M. Shapiro, D.C. Struppa1, A. Vajiac (2012), CUBO A Mathematical Journal, Vol. 14, No 2, (61-80). June 2012.
Adriaen Verheyleweghen, (2014) Computation of higher-order derivatives using the multi-complex step method, Project report, NTNU
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file numdifftools-0.9.20.tar.gz.
File metadata
- Download URL: numdifftools-0.9.20.tar.gz
- Upload date:
- Size: 3.0 MB
- Tags: Source
- Uploaded using Trusted Publishing? No
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a6af9a28851cc9a207720d949b34b6ac70f0bccb365d9df3c6ef3ffd91176257
|
|
| MD5 |
c0545b8d1d1b4cdd1d5dacd99ff42666
|
|
| BLAKE2b-256 |
70251af07d513fc5fb60b80c4577971fdd3480f931291f783dde33de178b185f
|
File details
Details for the file numdifftools-0.9.20-py2.py3-none-any.whl.
File metadata
- Download URL: numdifftools-0.9.20-py2.py3-none-any.whl
- Upload date:
- Size: 3.2 MB
- Tags: Python 2, Python 3
- Uploaded using Trusted Publishing? No
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
443b43e43c970b4f37cd2a5a57f842192da89daa2d58105ca5f5f894b7d4fcd0
|
|
| MD5 |
9a4dc965e20d4fa8b0fd983ae970063e
|
|
| BLAKE2b-256 |
3fb2a492a473c3bcdfe8889986beb331e7198a718282de8c0ec8c9fec947878c
|



















