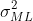A spatial lag operator proposal implemented in Python27: only the k-nearest neighbor (oknn), PyOKNN.
Project description
PyOKNN - A spatial lag operator proposal implemented in Python: only the k-nearest neighbor (oknn).
Why
By opposition to the time-series case, specifying the spatial lag operator involves a lot of arbitrariness. Hence this proposal, which yields a lag operator usable as primarily observed without modifications. (click to expand)
Fingleton (2009) and Corrado and Fingleton (2012) remind the analogies between temporal and spatial processes, at least when considering their lag operators. In the spatial econometric (SE) case, the lag operator is always explicitly involved via the use of a 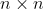

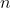
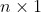
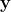
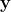
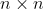
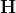
The so-structured data generating process (DGP) thus involves 
By opposition to the time series (TS) case, specifying 







But the choice of 





Hence the proposal that follows, i.e a specification method for the spatial lag operator whose properties are as close as possible to the ones of its time series (TS) counterpart, i.e. usable as primarily observed without modifications. Nonetheless we follow Pinkse and Slade (2010, p.105)’s recommendation of developing tools that are not simply extensions of familiar TS techniques to multiple dimensions. This is done so by proposing a specification-method which is fully grounded on the observation of the empirical characteristics of space, while minimizing as much as possible the set of hypotheses that are required.
Whereas the oknn specification of 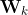
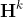
This specification implies the transposition in space of the three-stage modeling approach of Box and Jenkins (1976) which consists of (i) identifying and selecting the model, (ii) estimating the parameters and (iii) checking the model. It follows that the models that are subject to selection in the present work are likely to involve a large number of parameters whose distributions, probably not symmetrical, are cumbersome to derive analytically. This is why in addition to the (normal-approximation-based) observed confidence intervals, (non-adjusted and adjusted) bootstrap percentile intervals are implemented. However, the existence of fixed spatial weight matrices prohibits the use of traditional bootstrapping methods. So as to compute (normal approximation or percentile-based) confidence intervals for all the parameters, we use a special case of bootstrap method, namely Lin et al. (2007)’s hybrid version of residual-based recursive wild bootstrap. This method is particularly appropriate since it (i) "accounts for fixed spatial structure and heteroscedasticity of unknown form in the data" and (ii) "can be used for model identification (pre-test) and diagnostic checking (post-test) of a spatial econometric model". As mentioned above, non-adjusted percentile intervals as well as bias-corrected and accelerated (BCa) percentile intervals (Efron and Tibshirani, 1993) are implemented as well.
How
Python2.7.+ requirements
- matplotlib (==1.4.3 preferably)
- numdifftools (>=0.9.20 preferably)
- numpy (>=1.14.0 preferably)
- pandas (>=0.22.0 preferably)
- scipy (>=1.0.0 preferably)
- pysal (>=1.14.3 preferably)
Installation
We are going to use a package management system to install and manage software packages written in Python, namely pip. Open a session in your OS shell prompt and type
pip install pyoknn
Or using a non-python-builtin approach, namely git,
git clone git://github.com/lfaucheux/PyOKNN.git
cd PyOKNN
python setup.py install
Example usage:
The example that follows is done via the Python Shell. Let's first import the module PyOKNN.
>>> import PyOKNN as ok
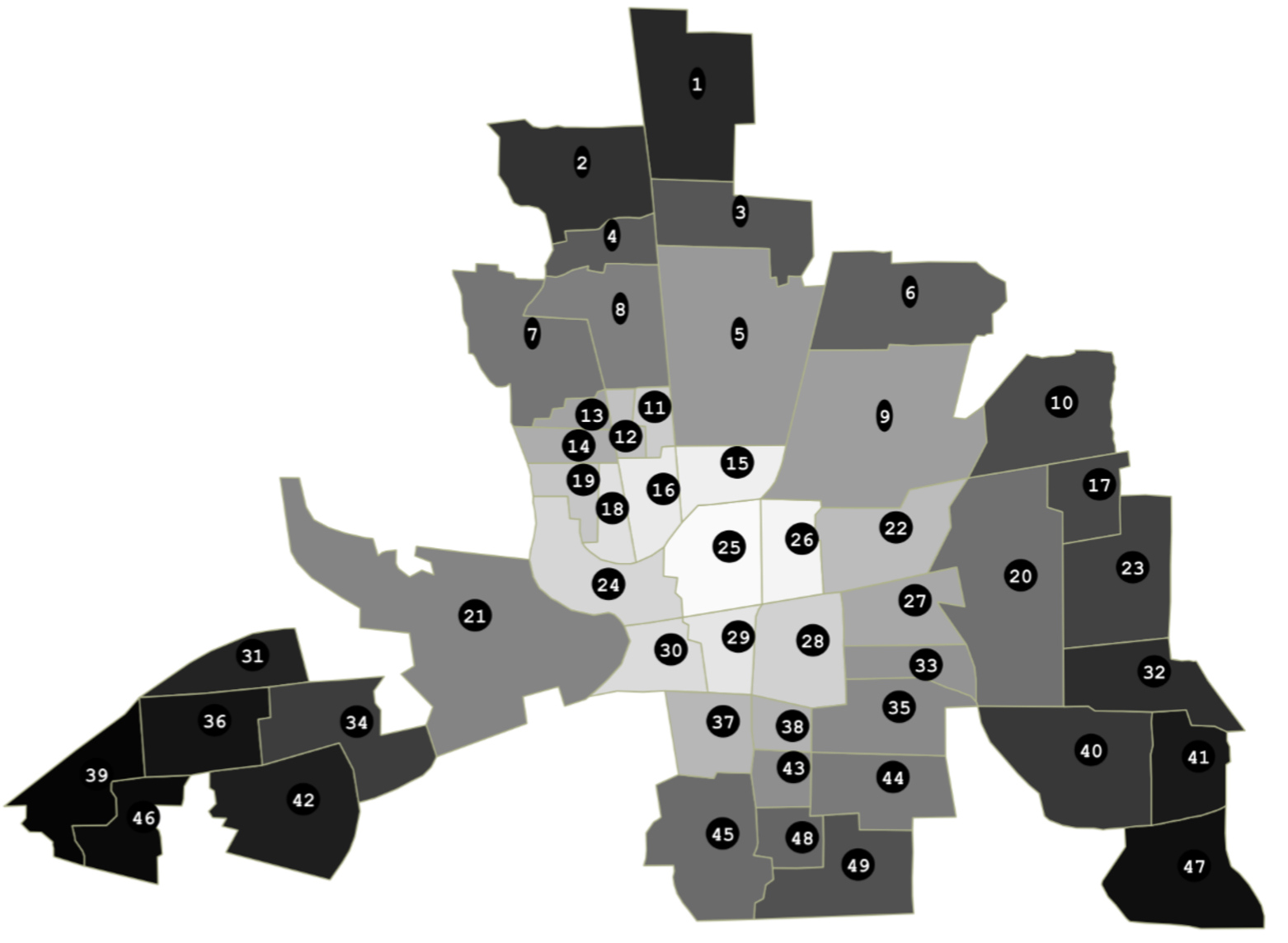
We use Anselin's Columbus OH 49 observation data set. Since the data set is included in PyOKNN, there is no need to mention the path directory.
>>> o = ok.Presenter(
... data_name = 'columbus',
... y_name = 'CRIME',
... x_names = ['INC', 'HOVAL'],
... id_name = 'POLYID',
... verbose = True,
... opverbose = True,
... )
Let's directly illustrate the main raison d'être of this package, i.e. modelling spatial correlation structures. To do so, simply type
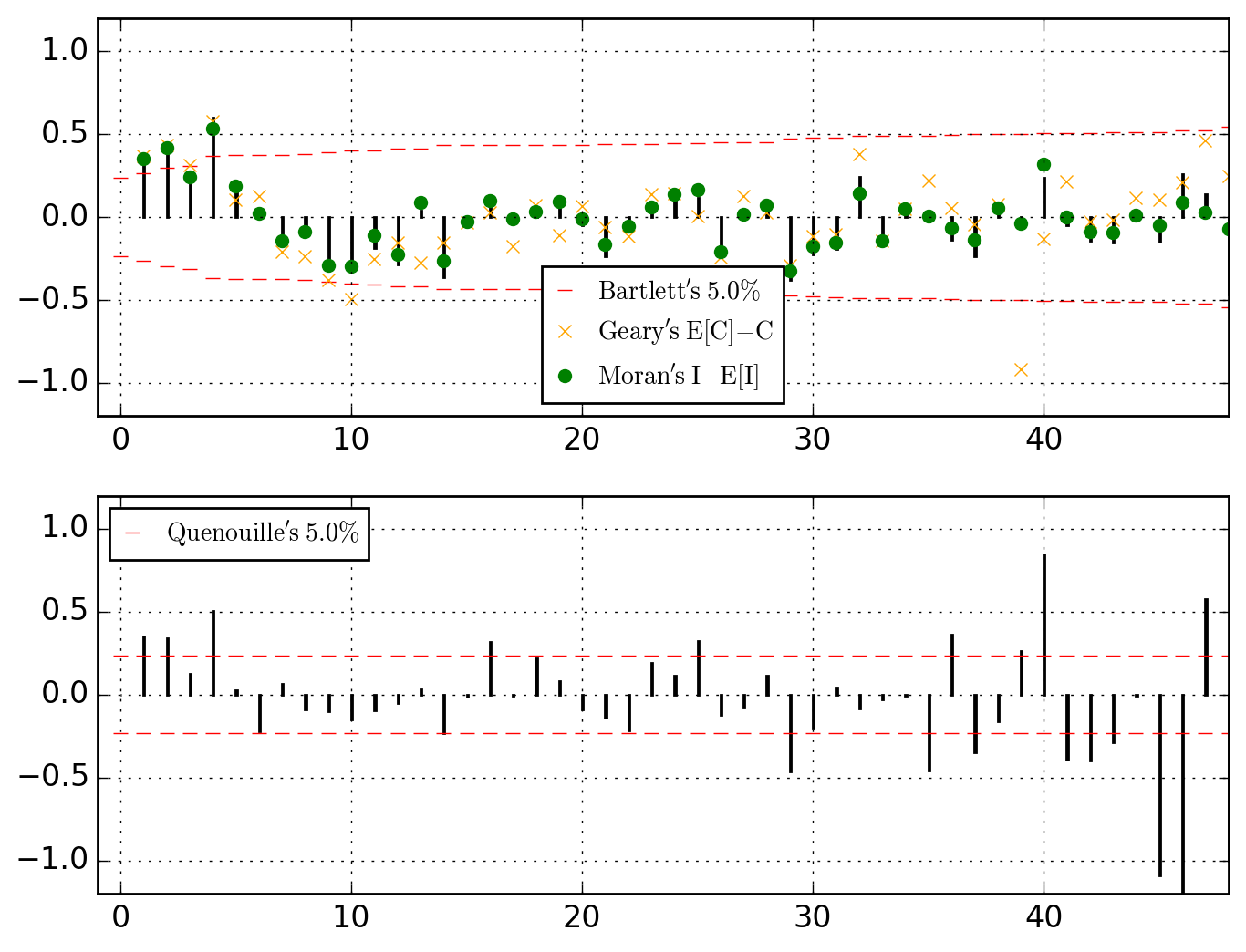
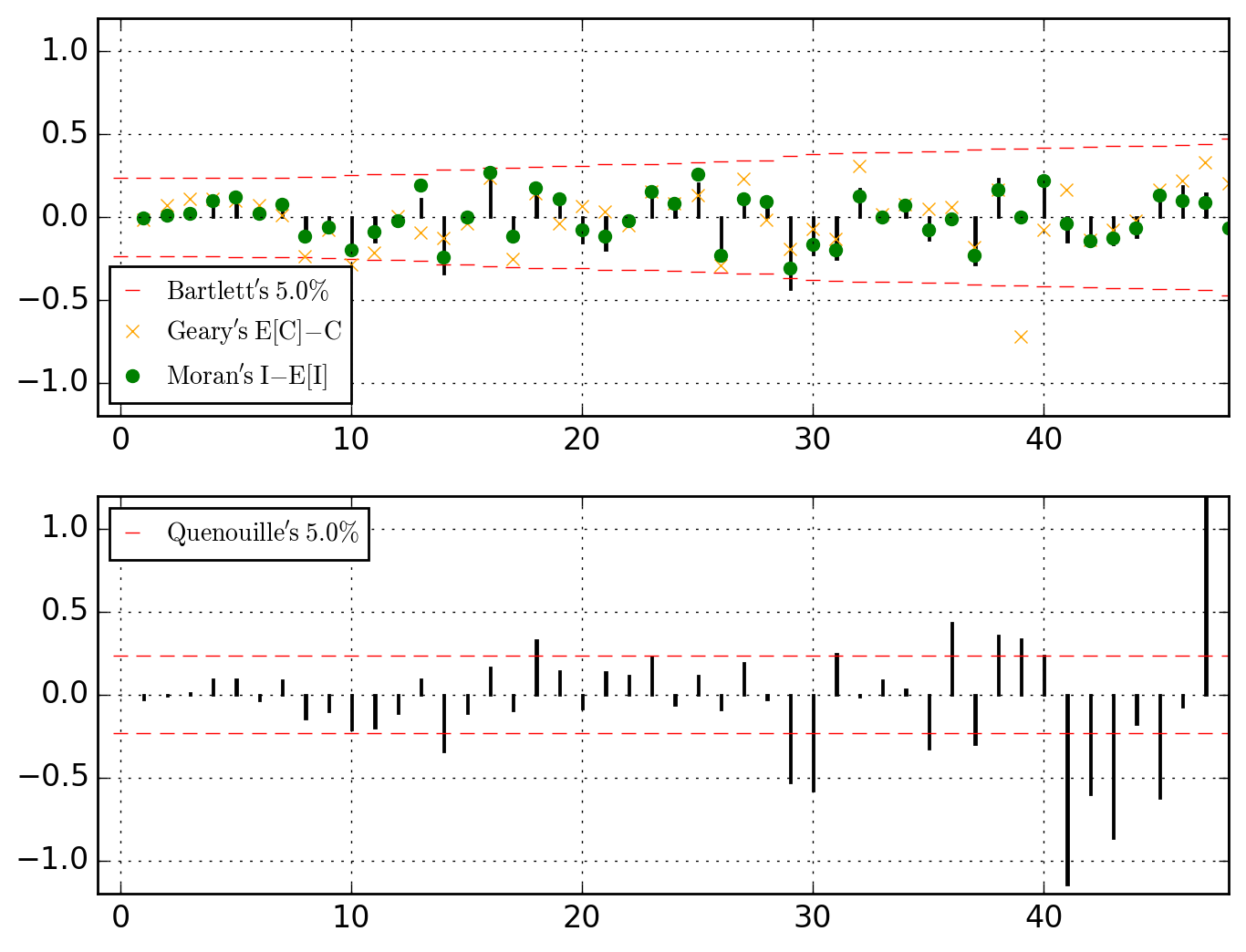
>>> o.u_XACF_chart
saved in C:\data\Columbus.out\ER{0}AR{0}MA{0}[RESID][(P)ACF].png
and
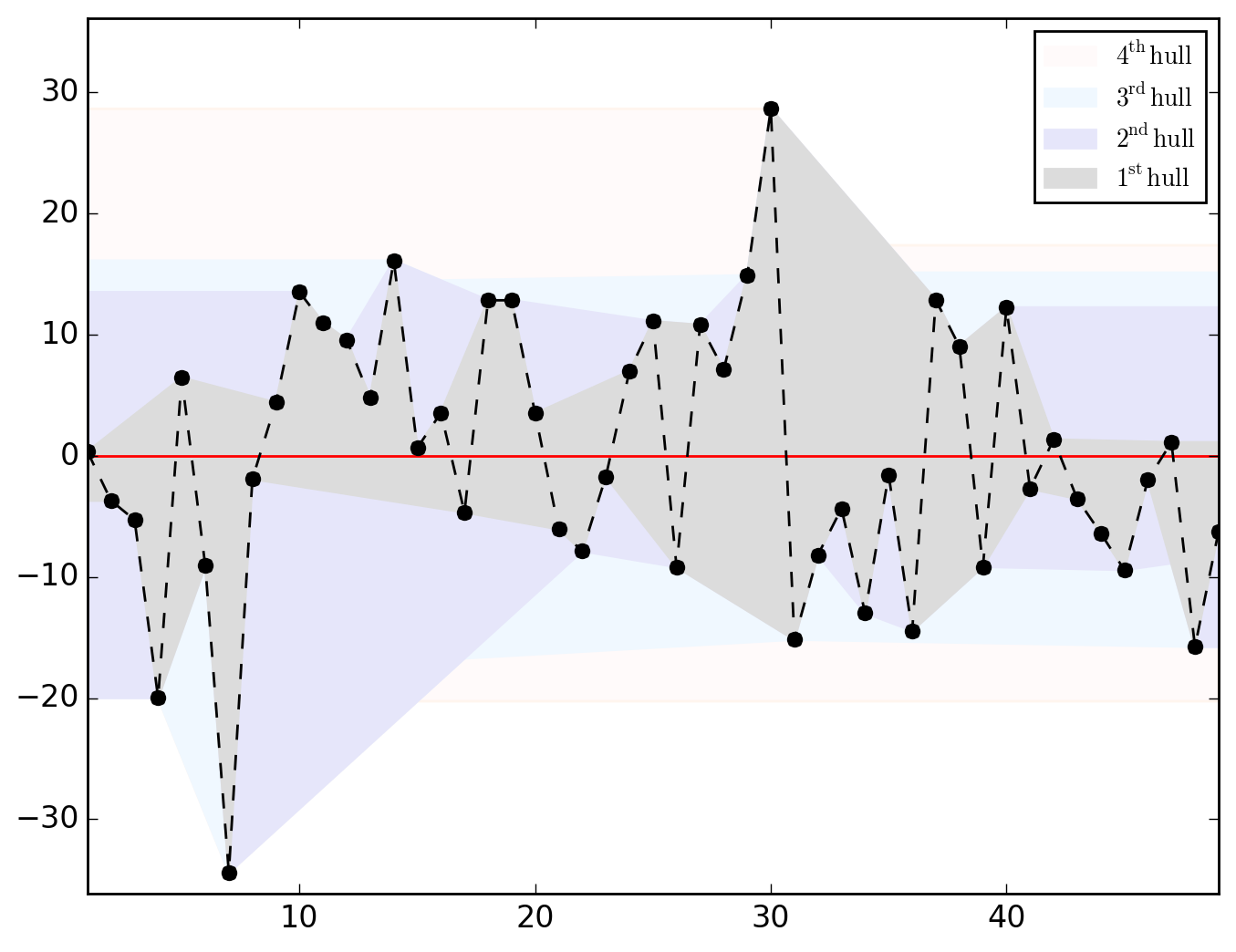
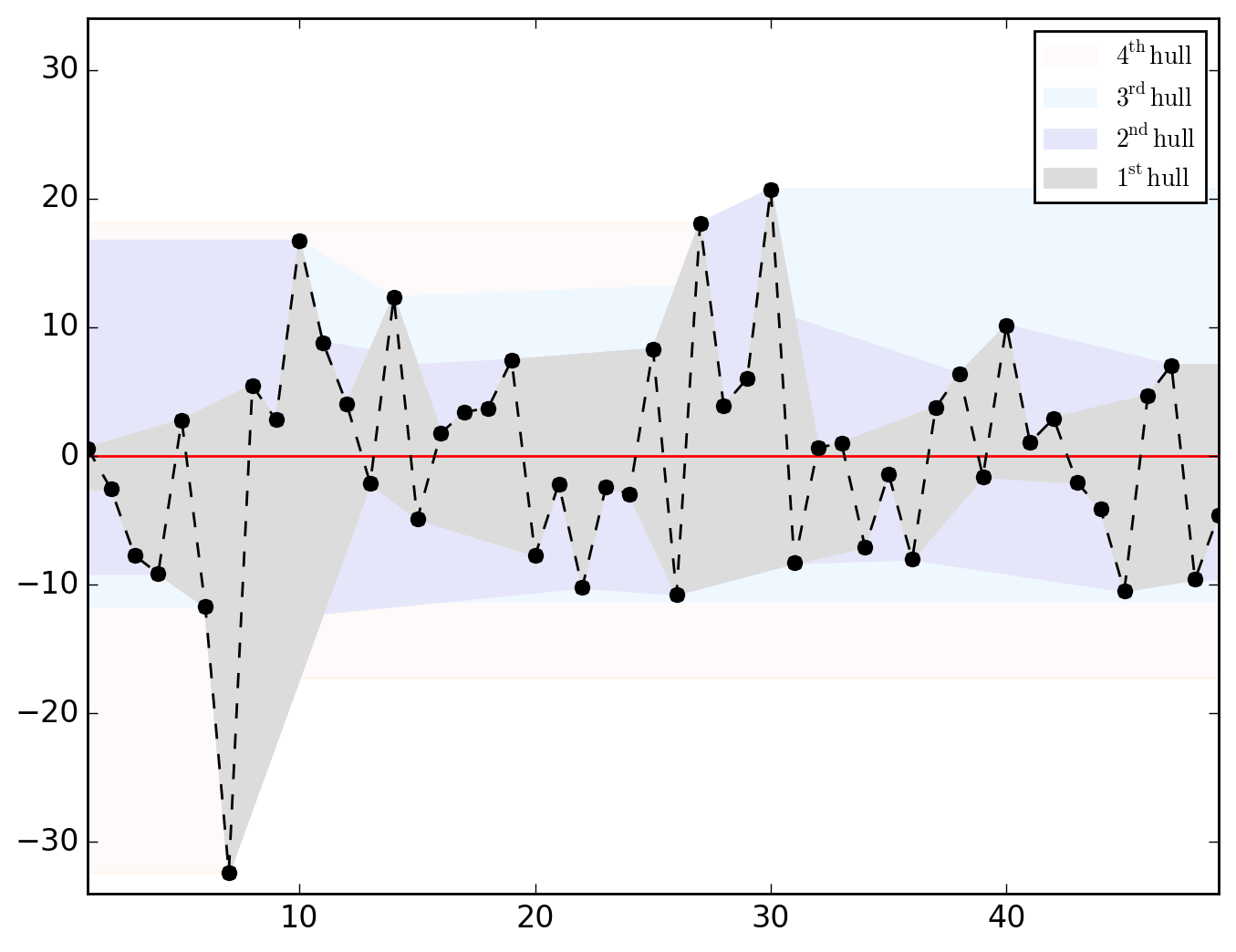
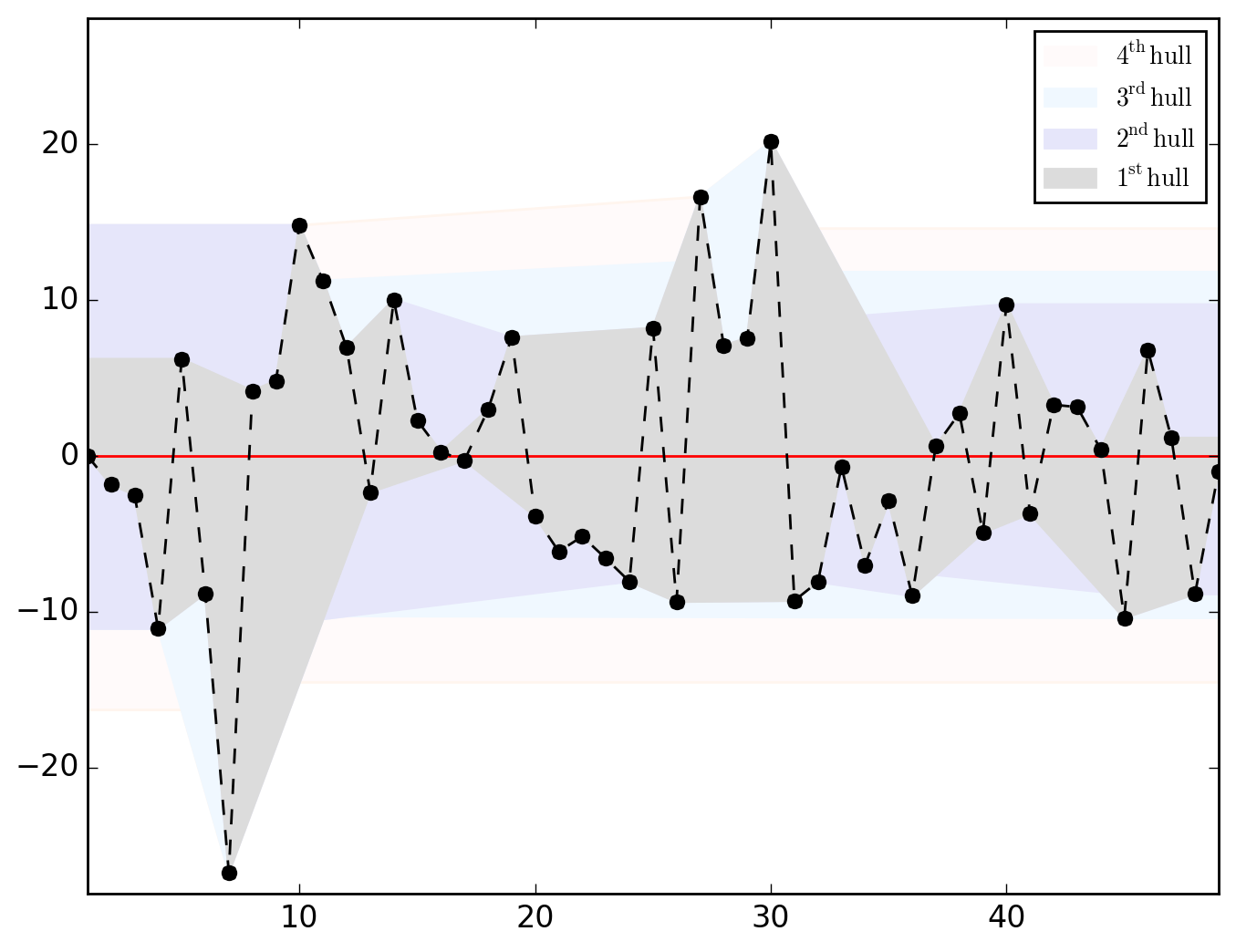
>>> o.u_hull_chart
saved in C:\data\Columbus.out\ER{0}AR{0}MA{0}[RESID][HULLS].png
ER{0}AR{0}MA{0}[RESID][(P)ACF].png and ER{0}AR{0}MA{0}[RESID][HULLS].png look like this
N.B.. (click to expand)
Hull charts should be treated with great caution since before talking about "long-distance trend" and/or "space-dependent variance", we should make sure that residuals are somehow sorted geographically. However, as shown in the map below, saying that it is totally uninformative appears abusive.
Be it in the ACF (upper dial) or in the PACF, we clearly have significant dependences at work through the lags 1, 2 and 4. Let's first think of it as global (thus considering the PACF) and go for an AR{1,2,4}.
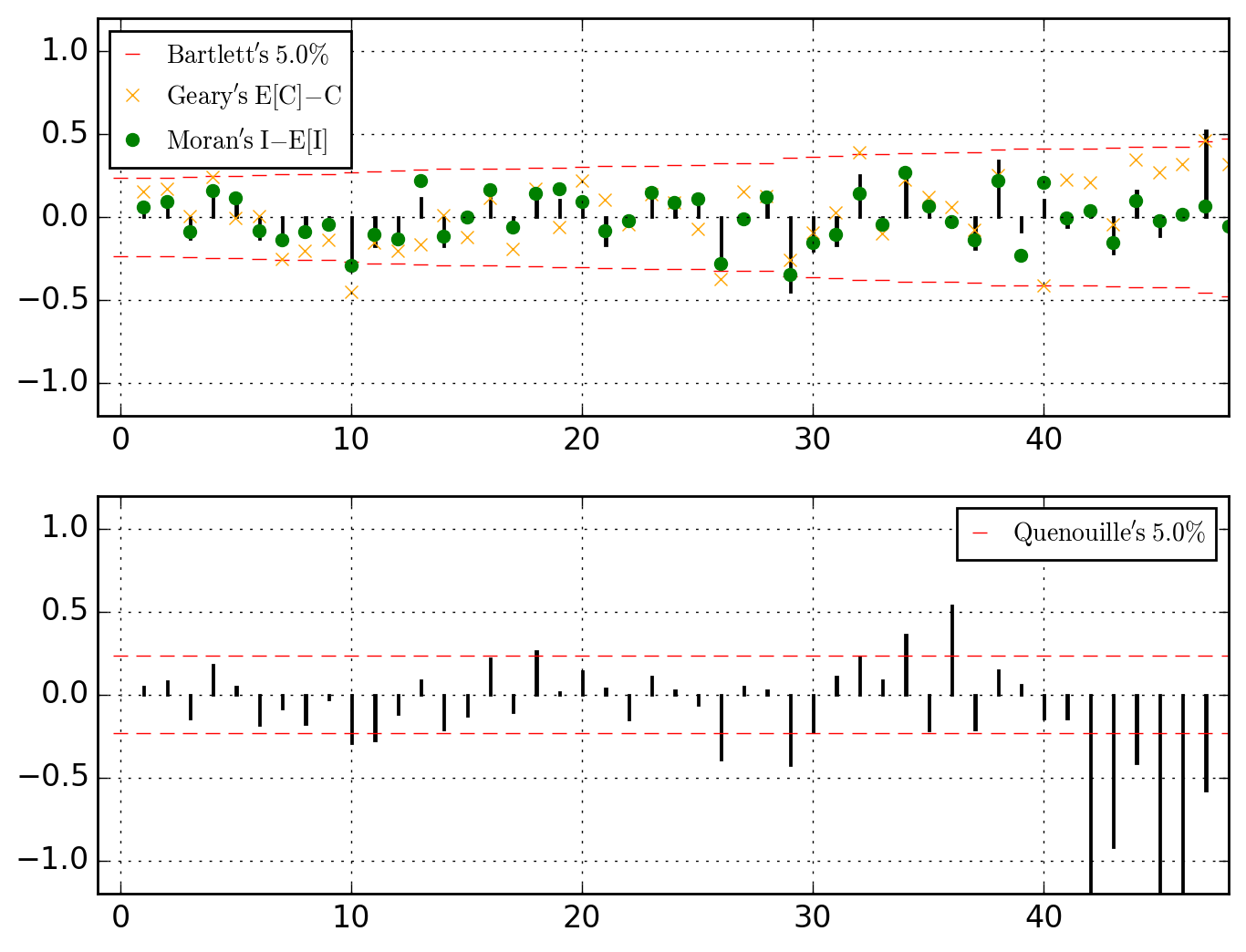
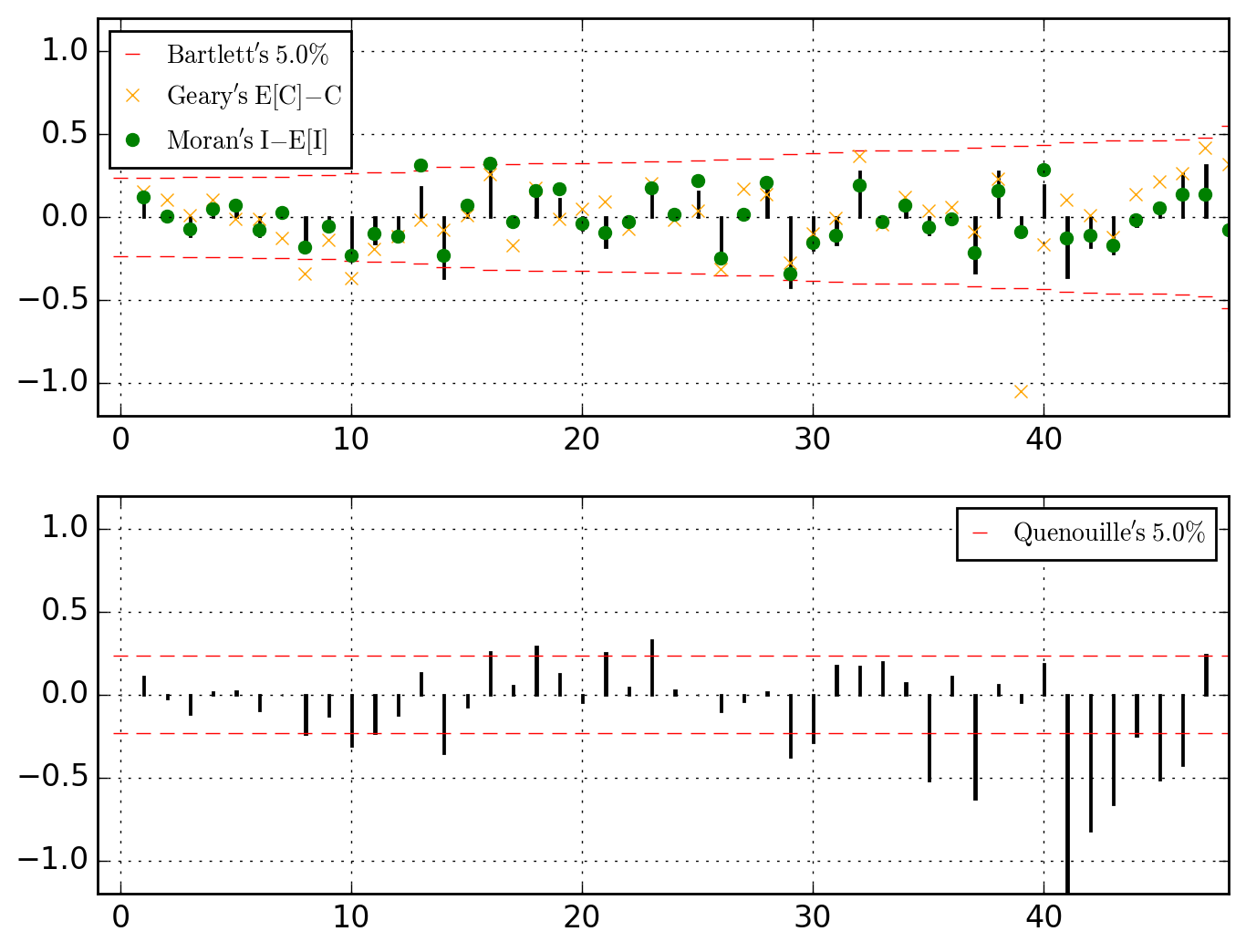
>>> o.u_XACF_chart_of(AR_ks=[1, 2, 4])
Optimization terminated successfully.
Current function value: 108.789436
Iterations: 177
Function evaluations: 370
saved in C:\data\Columbus.out\ER{0}AR{1,2,4}MA{0}[RESID][(P)ACF].png
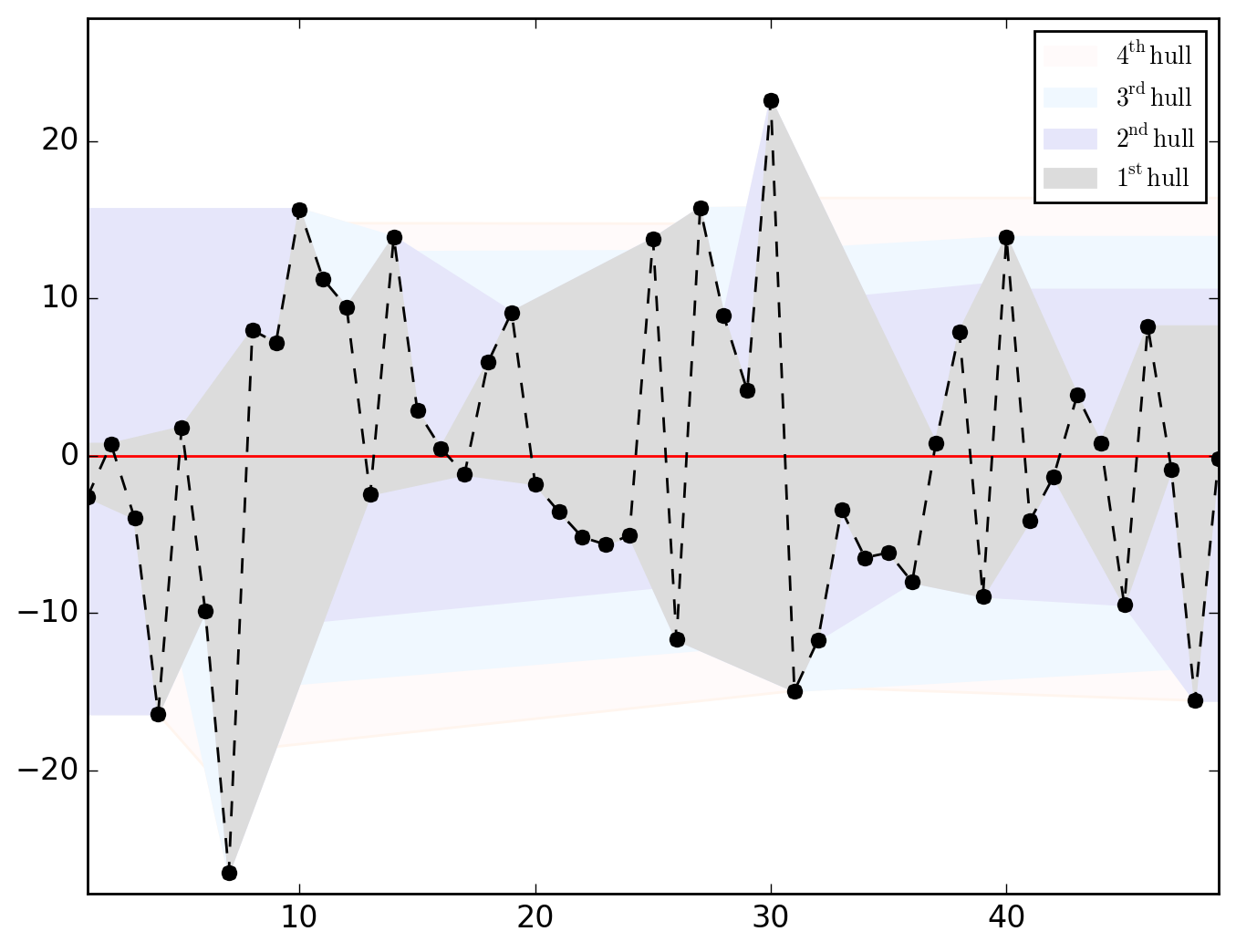
>>> o.u_hull_chart
saved in C:\data\Columbus.out\ER{0}AR{1,2,4}MA{0}[RESID][HULLS].png
or thinking of those as local, let's go for a MA{1,2,4}.
>>> o.u_XACF_chart_of(MA_ks=[1, 2, 4])
Optimization terminated successfully.
Current function value: 107.015463
Iterations: 174
Function evaluations: 357
saved in C:\data\Columbus.out\ER{0}AR{0}MA{1,2,4}[RESID][(P)ACF].png
>>> o.u_hull_chart
saved in C:\data\Columbus.out\ER{0}AR{0}MA{1,2,4}[RESID][HULLS].png
Thinking of CRIME variable as cointegrated through space with INC and HOVAL, let's run a (partial) differencing whose structure is superimposed to the lags 1, 2 and 4.
>>> o.u_XACF_chart_of(ER_ks=[1, 2, 4])
Optimization terminated successfully.
Current function value: 107.126738
Iterations: 189
Function evaluations: 382
saved in C:\data\Columbus.out\ER{1,2,4}AR{0}MA{0}[RESID][(P)ACF].png
>>> o.u_hull_chart
saved in C:\data\Columbus.out\ER{1,2,4}AR{0}MA{0}[RESID][HULLS].png
A little summary is always useful.
>>> o.summary()
================================= PARS
\\\\ HAT //// ER{0}AR{0}MA{0} ER{0}AR{0}MA{1,2,4} ER{0}AR{1,2,4}MA{0} ER{1,2,4}AR{0}MA{0}
\beta_0 68.618961 63.418312 40.602532 59.163974
\beta_{HOVAL} -0.273931 -0.290030 -0.261453 -0.251289
\beta_{INC} -1.597311 -1.237462 -0.936830 -1.147231
\gamma_{1} NaN NaN NaN 0.106979
\gamma_{2} NaN NaN NaN 0.212151
\gamma_{4} NaN NaN NaN 0.377095
\lambda_{1} NaN 0.233173 NaN NaN
\lambda_{2} NaN 0.303743 NaN NaN
\lambda_{4} NaN 0.390871 NaN NaN
\rho_{1} NaN NaN 0.137684 NaN
\rho_{2} NaN NaN 0.218272 NaN
\rho_{4} NaN NaN 0.144365 NaN
\sigma^2_{ML} 122.752913 93.134974 79.000511 69.257032
================================= CRTS
\\\\ HAT //// ER{0}AR{0}MA{0} ER{0}AR{0}MA{1,2,4} ER{0}AR{1,2,4}MA{0} ER{1,2,4}AR{0}MA{0}
llik -187.377239 -176.543452 -178.317424 -176.654726
HQC 382.907740 369.393427 372.941372 369.615976
BIC 386.429939 376.437825 379.985770 376.660374
AIC 380.754478 365.086903 368.634848 365.309452
AICg 5.625770 5.306023 5.378430 5.310565
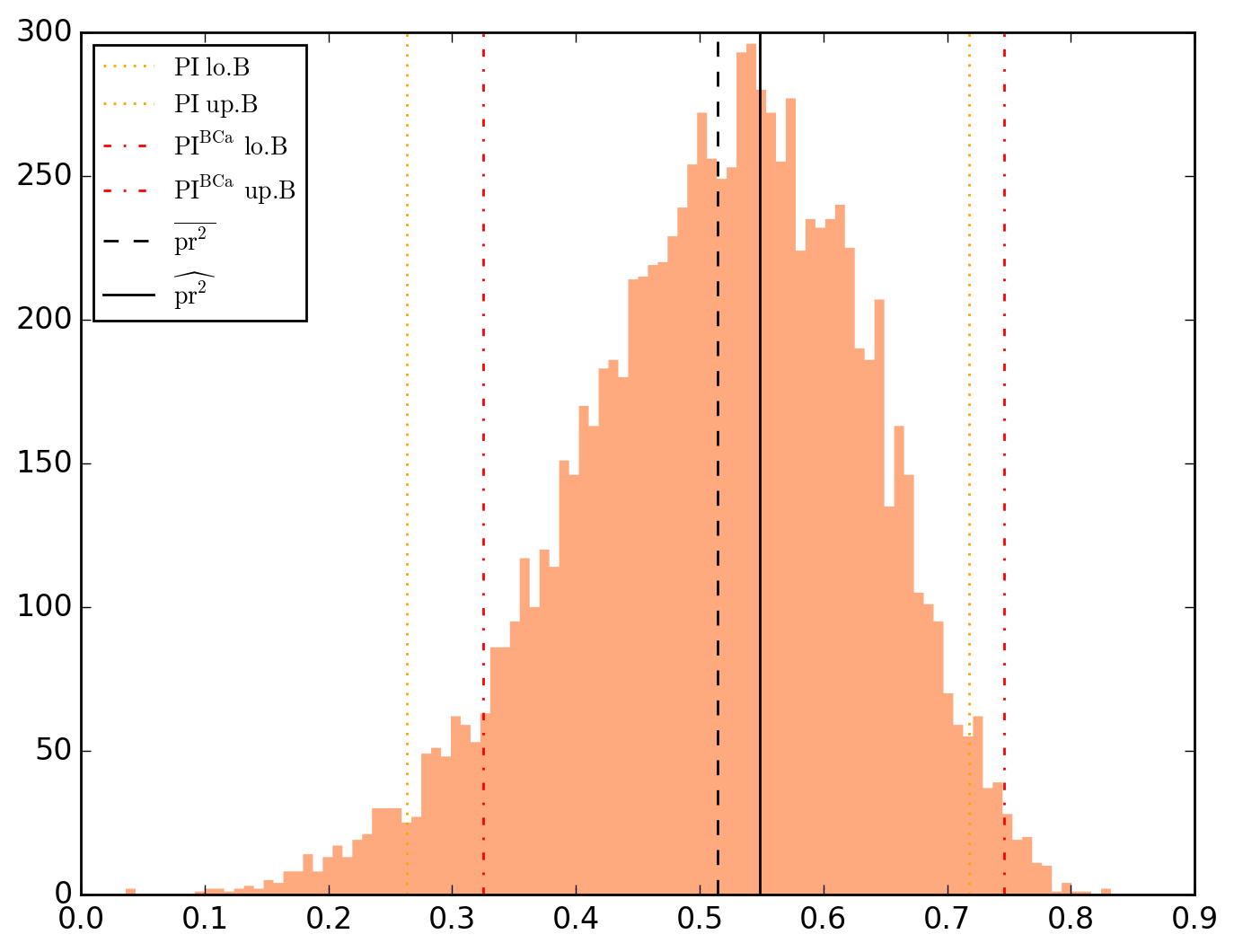
pr^2 0.552404 0.548456 0.542484 0.550022
pr^2 (pred) 0.552404 0.548456 0.590133 0.550022
Sh's W 0.977076 0.990134 0.949463 0.972979
Sh's Pr(>|W|) 0.449724 0.952490 0.035132 0.316830
Sh's W (pred) 0.977076 0.978415 0.969177 0.973051
Sh's Pr(>|W|) (pred) 0.449724 0.500748 0.224519 0.318861
BP's B 7.900442 2.778268 20.419370 9.983489
BP's Pr(>|B|) 0.019250 0.249291 0.000037 0.006794
KB's K 5.694088 2.723948 9.514668 6.721746
KB's Pr(>|K|) 0.058016 0.256155 0.008588 0.034705
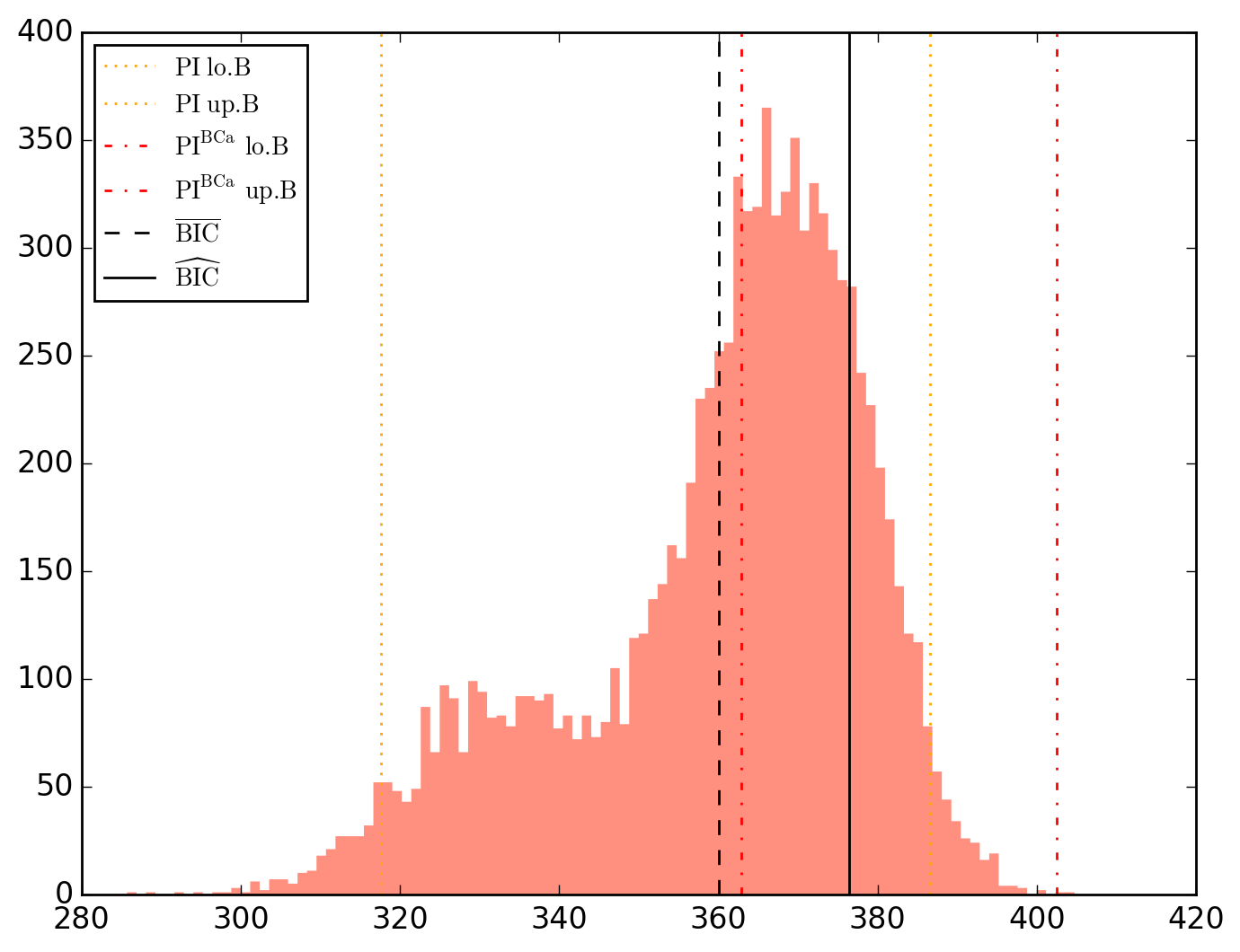
Given that the specification ER{0}AR{0}MA{1,2,4} has the minimum BIC, let's pursue with it and check its parameters-covariance matrix and statistical table. Keep in mind that the returned statistics and results are always those of the last model we worked with. We can figure out what this last model is -- i.e. the ongoing model --, typing
>>> o.model_id
ER{1,2,4}AR{0}MA{0}
Since we want to continue with the specification ER{0}AR{0}MA{1,2,4}, we thus have to explicitly set it as "ongoing". This can be done, say, while requesting the parameters-covariance matrix and statistical table, as follows
>>> o.covmat_of(MA_ks=[1, 2, 4])
\\\\ COV //// \beta_0 \beta_{INC} \beta_{HOVAL} \lambda_{1} \lambda_{2} \lambda_{4} \sigma^2_{ML}
\beta_0 19.139222 -0.784264 -0.025163 -0.061544 -0.028639 0.073201 -1.621429
\beta_{INC} -0.784264 0.109572 -0.019676 0.008862 0.017765 -0.014063 0.715907
\beta_{HOVAL} -0.025163 -0.019676 0.007814 -0.001673 -0.006111 0.003102 -0.239979
\lambda_{1} -0.061544 0.008862 -0.001673 0.010061 -0.000185 -0.001523 0.346635
\lambda_{2} -0.028639 0.017765 -0.006111 -0.000185 0.014815 -0.001668 0.576185
\lambda_{4} 0.073201 -0.014063 0.003102 -0.001523 -0.001668 0.008075 0.092086
\sigma^2_{ML} -1.621429 0.715907 -0.239979 0.346635 0.576185 0.092086 394.737828
and
>>> o.table_test # no need to type `o.table_test_of(MA_ks=[1, 2, 4])`
\\\\ STT //// Estimate Std. Error t|z value Pr(>|t|) Pr(>|z|) 95.0% lo. 95.0% up.
\beta_0 63.418312 4.374840 14.496146 3.702829e-18 1.281465e-47 62.193379 64.643245
\beta_{INC} -1.237462 0.331017 -3.738367 5.422541e-04 1.852193e-04 -1.330145 -1.144779
\beta_{HOVAL} -0.290030 0.088398 -3.280974 2.056930e-03 1.034494e-03 -0.314781 -0.265279
\lambda_{1} 0.233173 0.100303 2.324690 2.487823e-02 2.008854e-02 0.205089 0.261257
\lambda_{2} 0.303743 0.121716 2.495501 1.649425e-02 1.257793e-02 0.269663 0.337823
\lambda_{4} 0.390871 0.089860 4.349759 8.232171e-05 1.362874e-05 0.365711 0.416032
\sigma^2_{ML} 93.134973 19.868010 4.687685 2.795560e-05 2.763129e-06 87.572032 98.697913
Incidentally, note that the above table holds for
>>> o.type_I_err
0.05
But one may want not to make any assumptions regarding spatial parameters distribution and favor an empirical approach by bootstrap-estimating all parameters as well as their (bias-corrected and accelerated - BCa) percentile intervals.
>>> o.opverbose = False # Printing minimizer's messages may slow down iterations
>>> o.PIs_computer(
... plot_hist = True, # Bootstrap distributions
... plot_conv = True, # Convergence plots
... MA_ks = [1, 2, 4]
... nbsamples = 10000 # Number of resamplings
... )
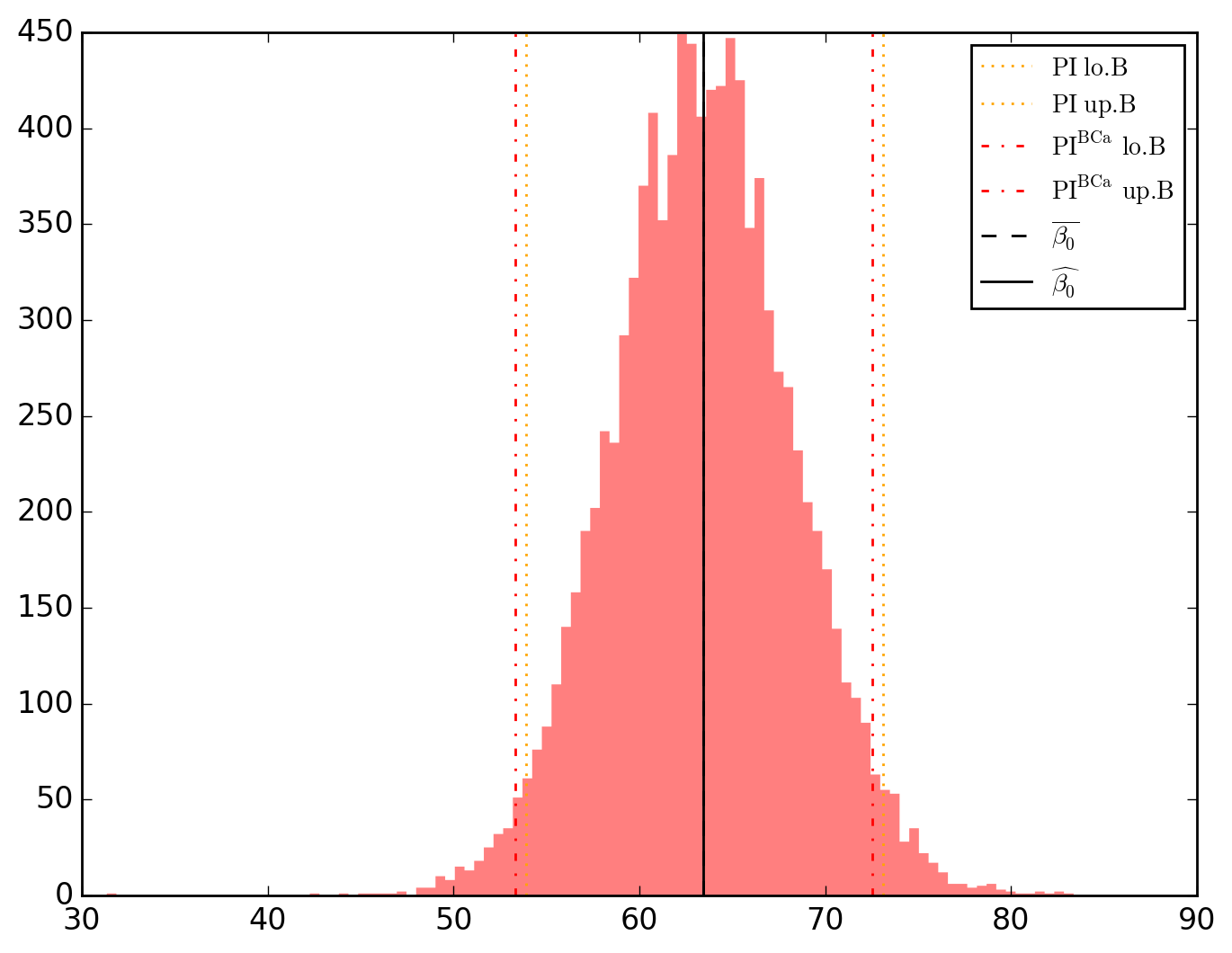
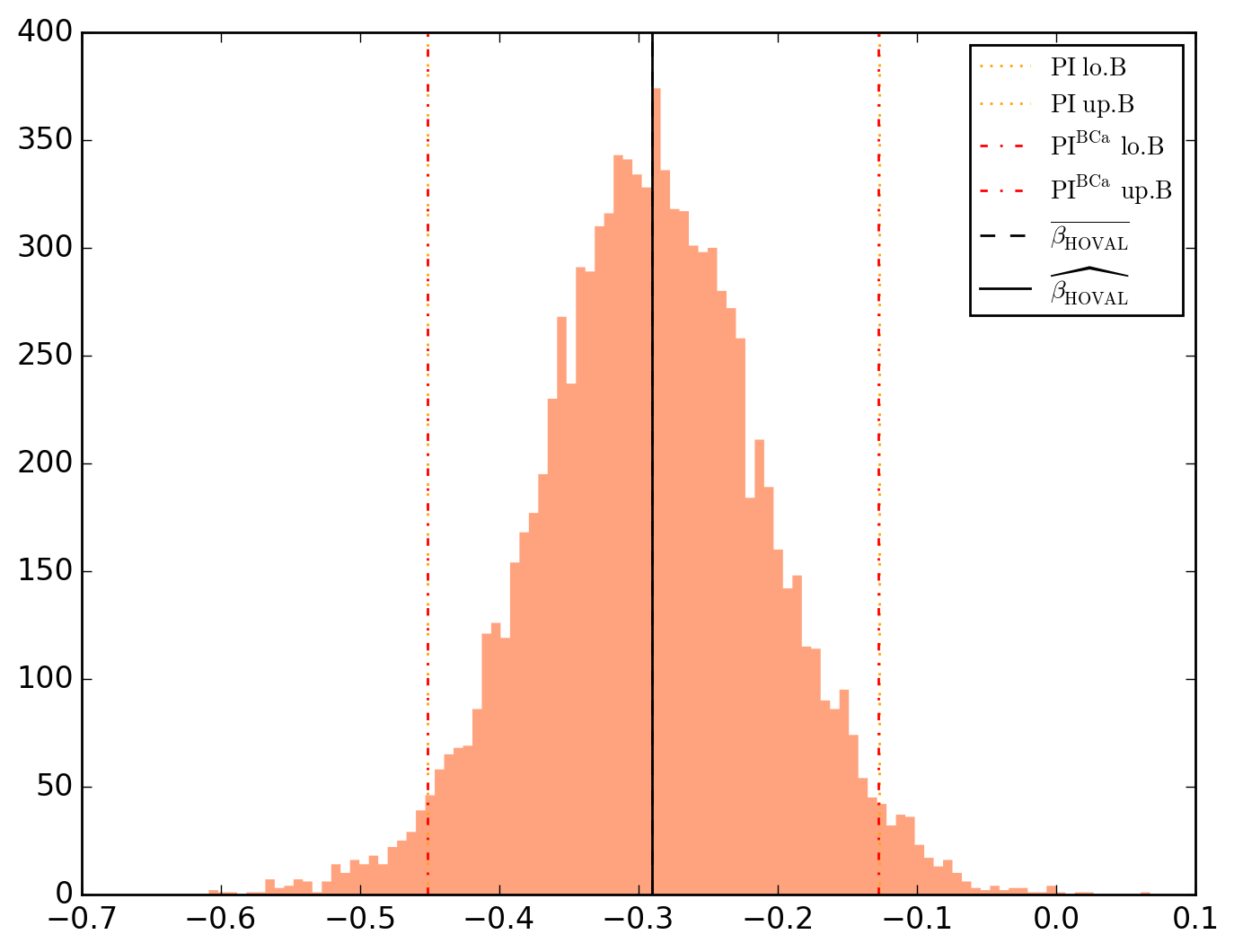
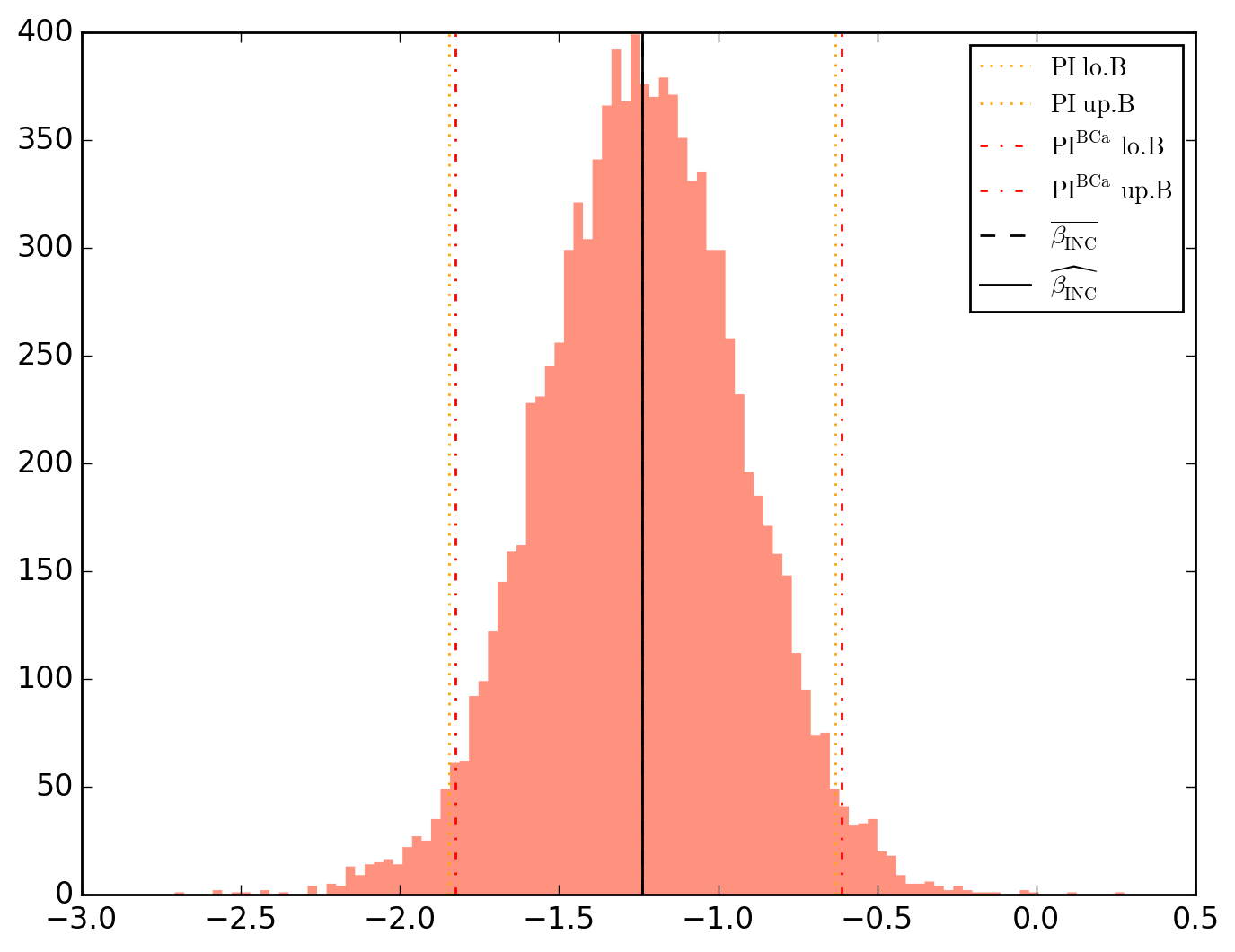
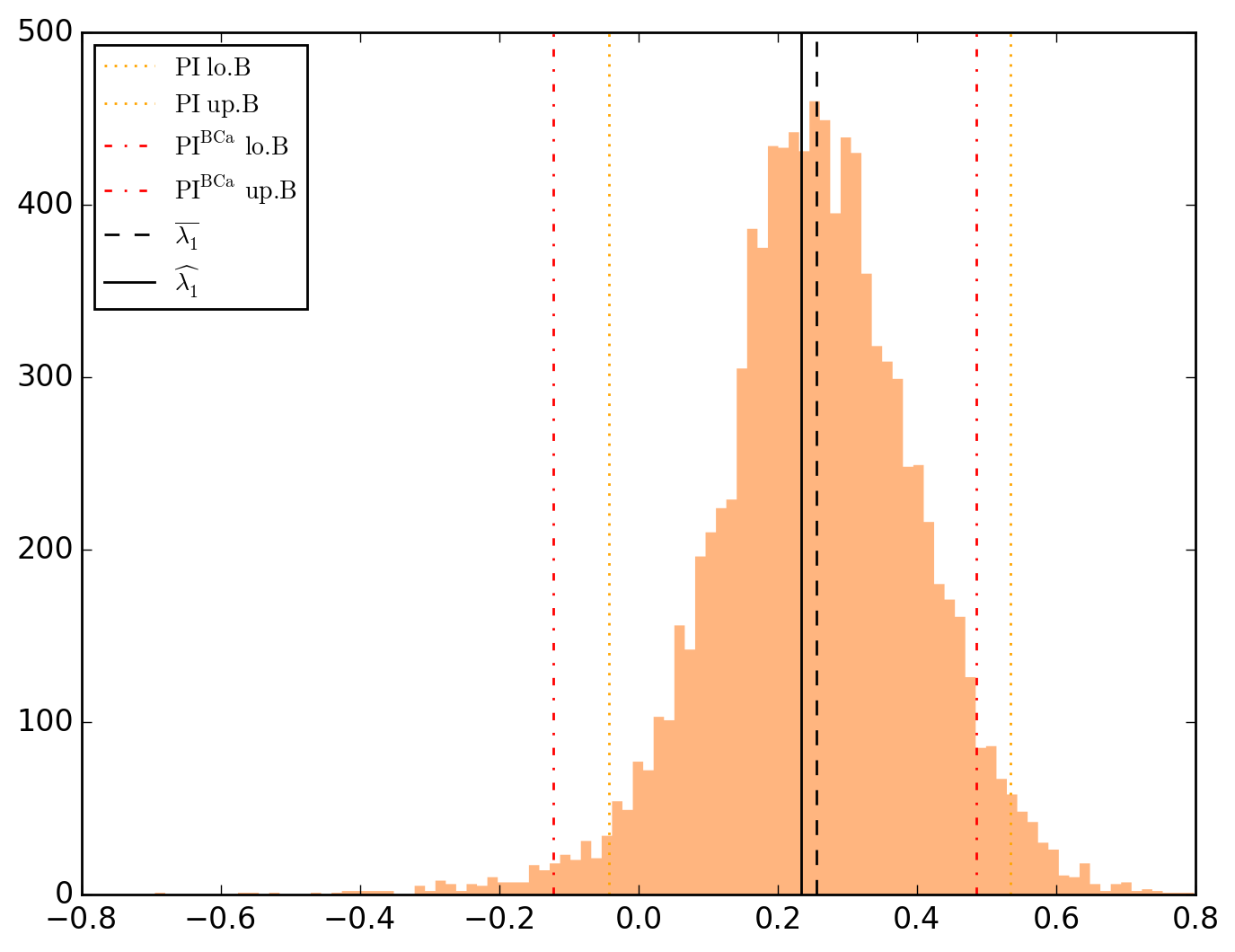
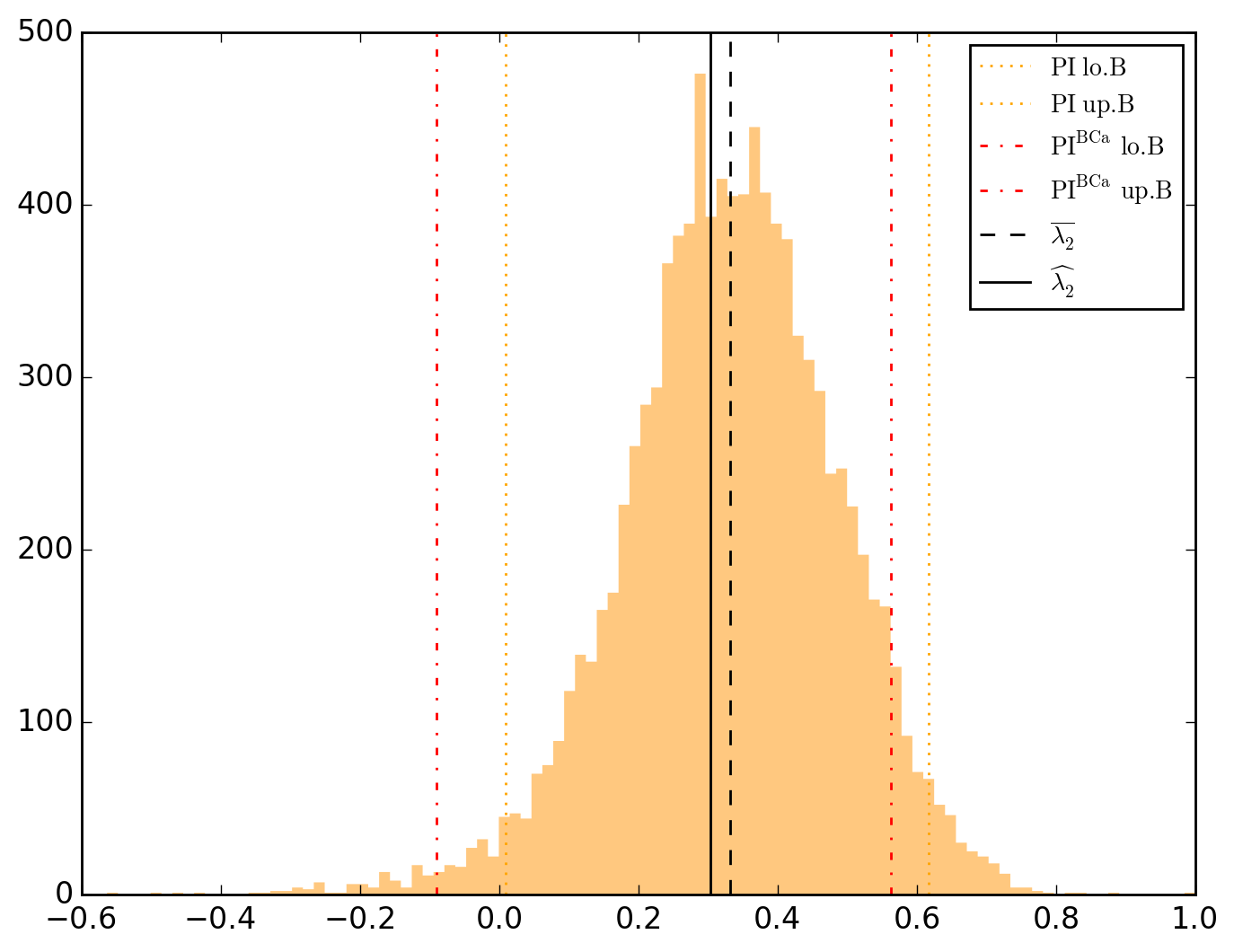
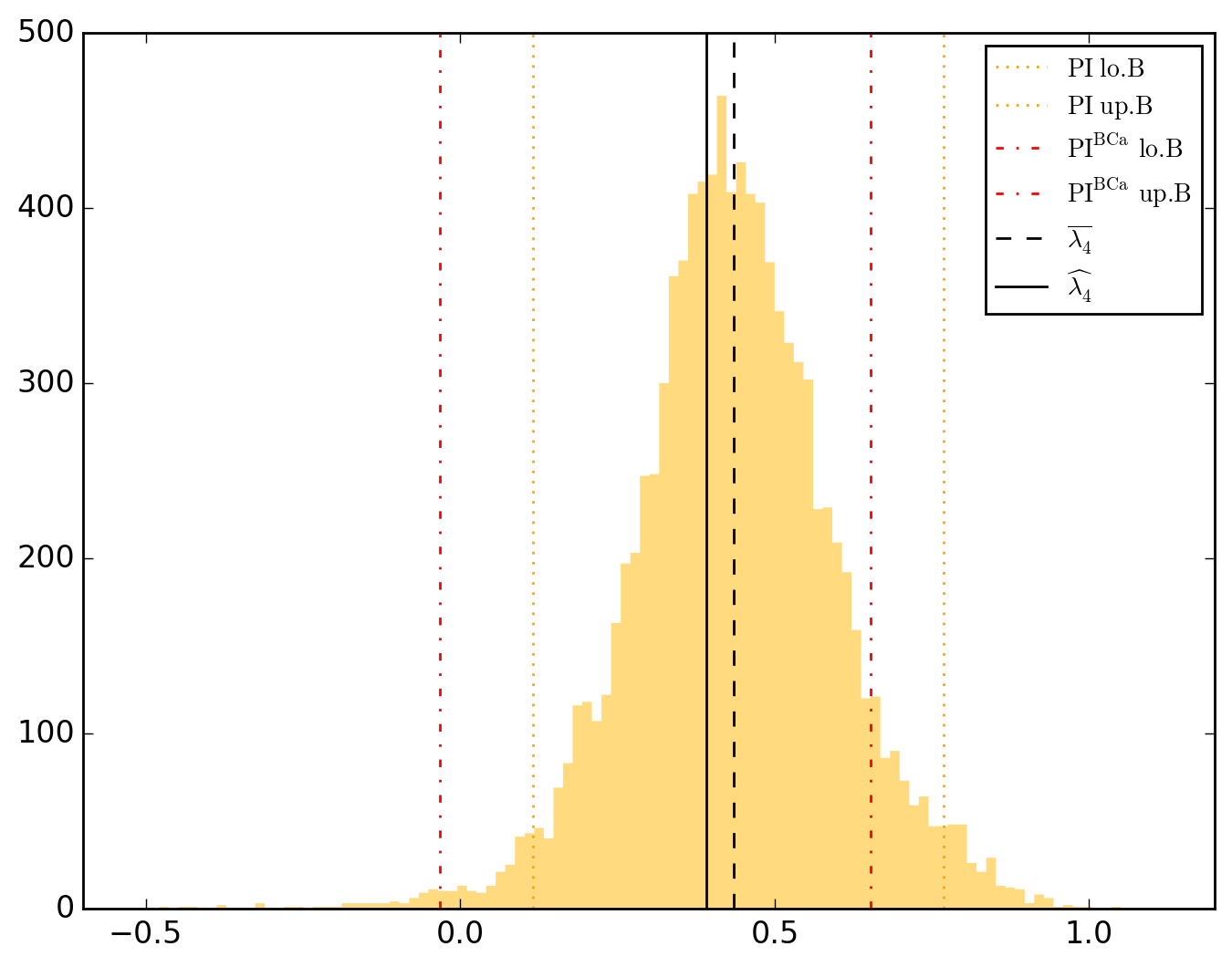
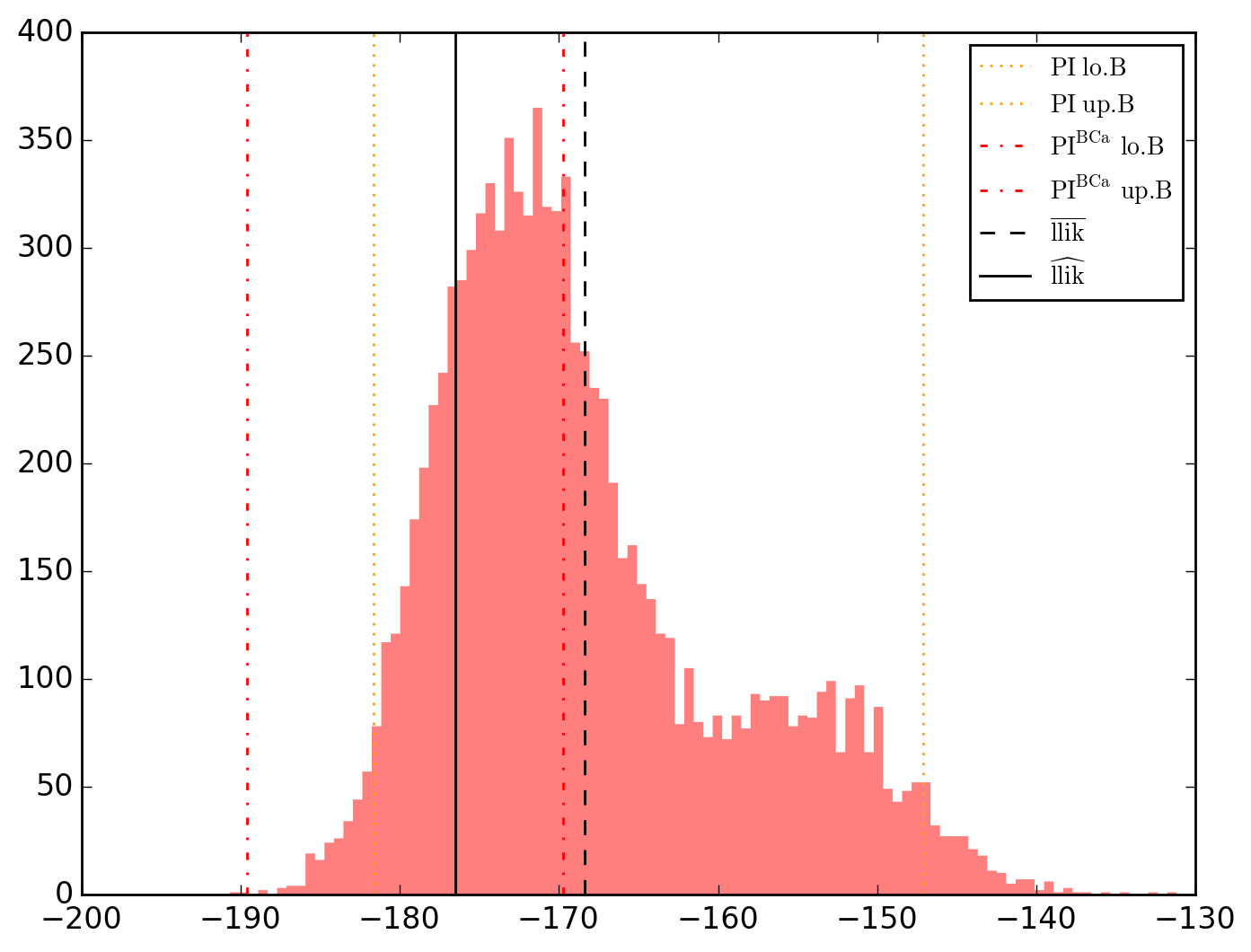
10000 resamplings later, we see regarding economic parameters that using normal-approximation-based confidence intervals is anything but "flat wrong", look:
which is not as true for spatial parameters:
One notable diffference is that BCa percentile intervals of 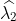
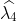
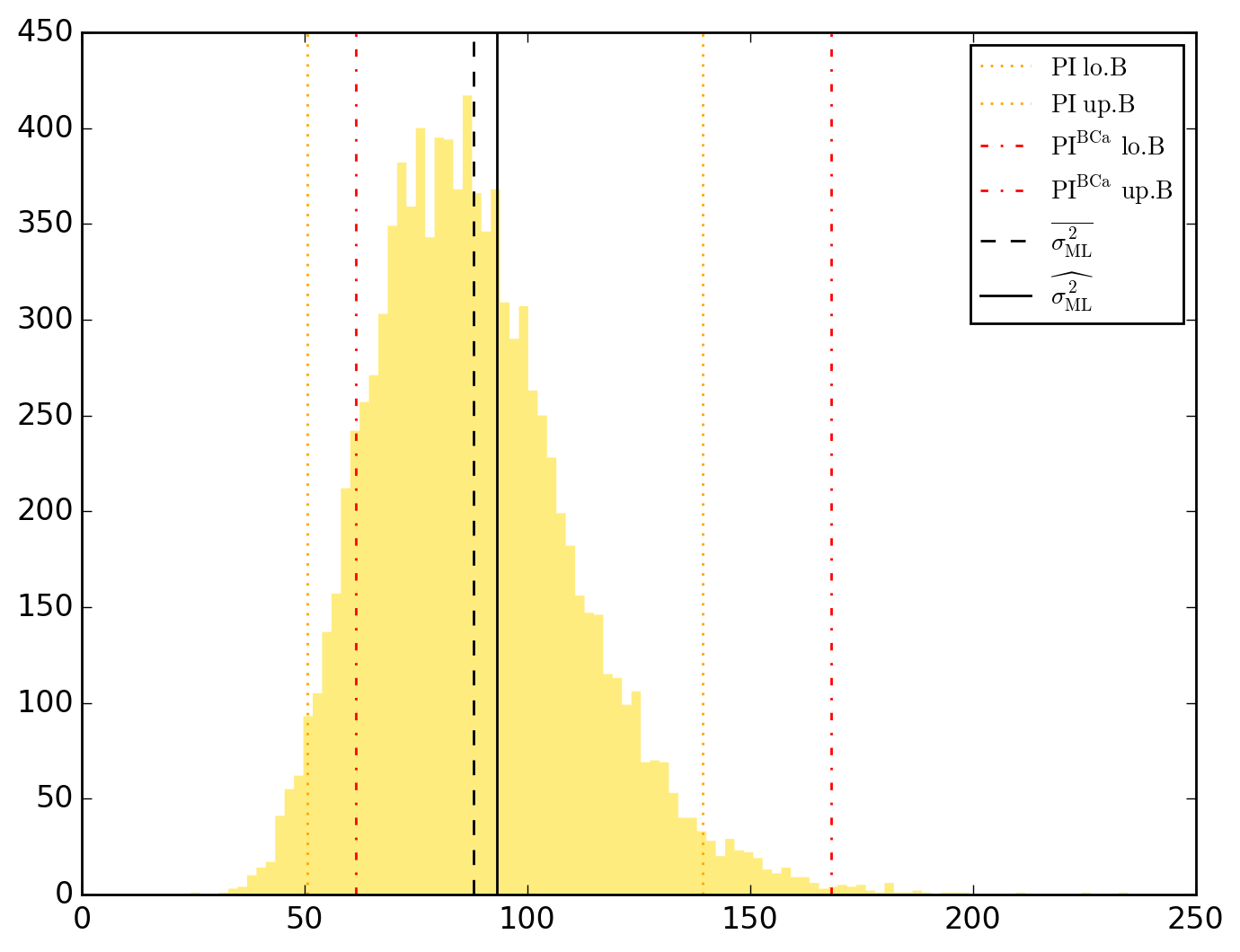
Note that the statistical table, previously called typing o.table_test, is now augmented on the right by the bootstrap-results.
>>> o.table_test
\\\\ STT //// Estimate Std. Error t|z value Pr(>|t|) Pr(>|z|) 95.0% CI.lo. 95.0% CI.up. 95.0% PI.lo. 95.0% PI.up. 95.0% BCa.lo. 95.0% BCa.up.
\beta_0 63.418312 4.374840 14.496146 3.702829e-18 1.281465e-47 62.193379 64.643245 53.922008 73.107011 53.328684 72.512817
\beta_{INC} -1.237462 0.331017 -3.738367 5.422541e-04 1.852193e-04 -1.330145 -1.144779 -1.846416 -0.632656 -1.825207 -0.610851
\beta_{HOVAL} -0.290030 0.088398 -3.280974 2.056930e-03 1.034494e-03 -0.314781 -0.265279 -0.451431 -0.127206 -0.451658 -0.127696
\lambda_{1} 0.233173 0.100303 2.324690 2.487823e-02 2.008854e-02 0.205089 0.261257 -0.043012 0.534407 -0.122474 0.484635
\lambda_{2} 0.303743 0.121716 2.495501 1.649425e-02 1.257793e-02 0.269663 0.337823 0.008517 0.616936 -0.089690 0.562511
\lambda_{4} 0.390871 0.089860 4.349759 8.232171e-05 1.362874e-05 0.365711 0.416032 0.116317 0.768369 -0.032977 0.652651
\sigma^2_{ML} 93.134973 19.868010 4.687685 2.795560e-05 2.763129e-06 87.572032 98.697913 50.668029 139.392307 61.426042 168.070074
Incidentally, other distributions have been generated in addition to those of the parameters
All the other charts (distributions and convergence plots) are viewable here.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file PyOKNN-0.1.66b0.tar.gz.
File metadata
- Download URL: PyOKNN-0.1.66b0.tar.gz
- Upload date:
- Size: 10.3 MB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.13.0 pkginfo/1.5.0.1 requests/2.18.4 setuptools/40.2.0 requests-toolbelt/0.8.0 tqdm/4.19.5 CPython/2.7.15
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
33cbb03511efcf5339298692868025ac293dbfd47b2f9e07d3ed35f511e50a9d
|
|
| MD5 |
4cba2513390f0f6255122760a8068a4a
|
|
| BLAKE2b-256 |
34ebecbd3730c91be78b4faae2fea0105a698530b6e681b81e662a9f1d70fe99
|
File details
Details for the file PyOKNN-0.1.66b0-py2-none-any.whl.
File metadata
- Download URL: PyOKNN-0.1.66b0-py2-none-any.whl
- Upload date:
- Size: 10.5 MB
- Tags: Python 2
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.13.0 pkginfo/1.5.0.1 requests/2.18.4 setuptools/40.2.0 requests-toolbelt/0.8.0 tqdm/4.19.5 CPython/2.7.15
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
1262bf892df9a2152d3f15080dd5920b49125bea98d452bb7d23476b61abc15f
|
|
| MD5 |
f2d21857c94c06dca1da76e3dd05aeb8
|
|
| BLAKE2b-256 |
c113abc1214f2e0a11980a189bc3b41ecdd2d4d209cce81783c7fda675fb3741
|