Big O calculations for Time
Project description
TimeComplex
This package was created to evaluate functions for time complexity. The function runs an algorithm over and over with randomized input sizes to judge the time complexity. PYPI: https://pypi.org/project/SpaceTimeComplex/
Example
def looper2(n):
for x in range(n):
print(x)
def testone(n):
for x in range(len(n)):
for y in range(len(n)):
for z in range(len(n)):
two = y
one = x
three = z
def looper(today,stringer):
for x in range(today):
print(x)
for y in stringer:
print(y)
def logfunc(n):
for x in range(0,len(n[0]),20):
print(x)
def binary_search(array,target):
low = 0
high = len(array) - 1
while low <= high:
mid = (low + high) // 2 # integer division
element = array[mid]
if element == target:
return mid
elif element < target:
low = mid + 1
else:
high = mid - 1
return -1
real = SpaceTimeComplex.RealTime() # Create the class
#x.realTimeComplex(stmt="looper(10)",value=10)
testSet = real.generateTestSet(size2=100) #generate a test set
testSet1 = [[4,"stnr=gwege"], [12,"sagsdgg"], [3,"esfsfsseafesfsefsef"], [45,"stnrefgseege"], [17,"sagwetjtwfwe"], [34,"esfsfssem"],[41,"stn"], [53,"sakhhksdgg"], [24,"esjfjkkfsefsef"], [70,"stnwete"], [7,"sagwefwewsdfsdffwe"] ]
# format of array. 2d array with each test set inside. You can make your own or just generate one with generateTestSet()
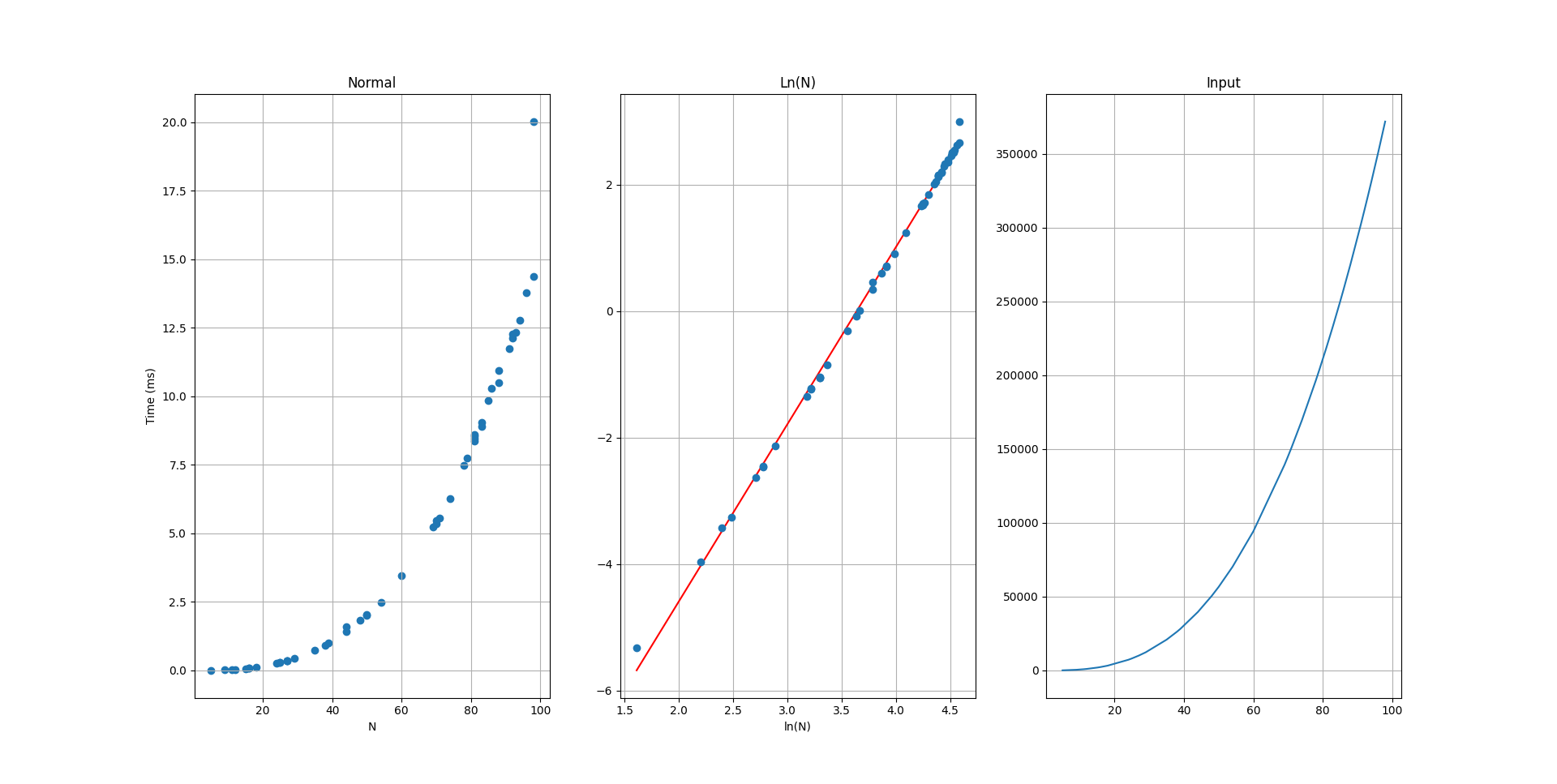
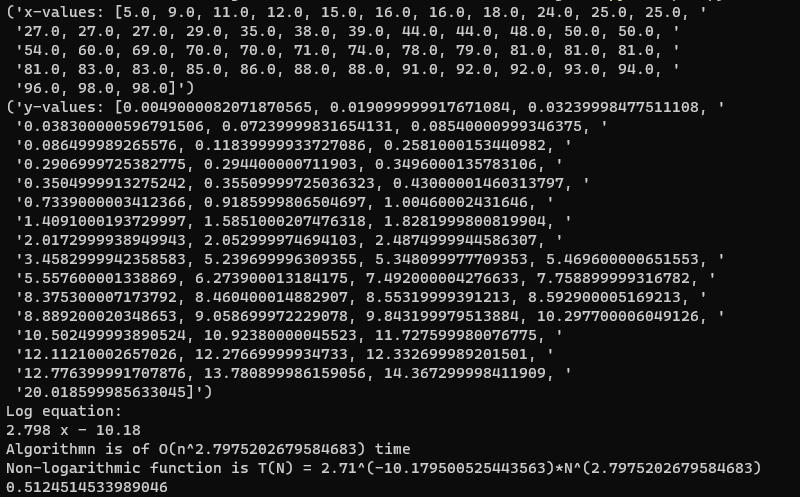
logFunction, SlopeConst = real.complexGuess(testone,testSet) #guess the complexity of a function. Returns the guess and a plot
ratio = real.bestWorst(testone,testSet)
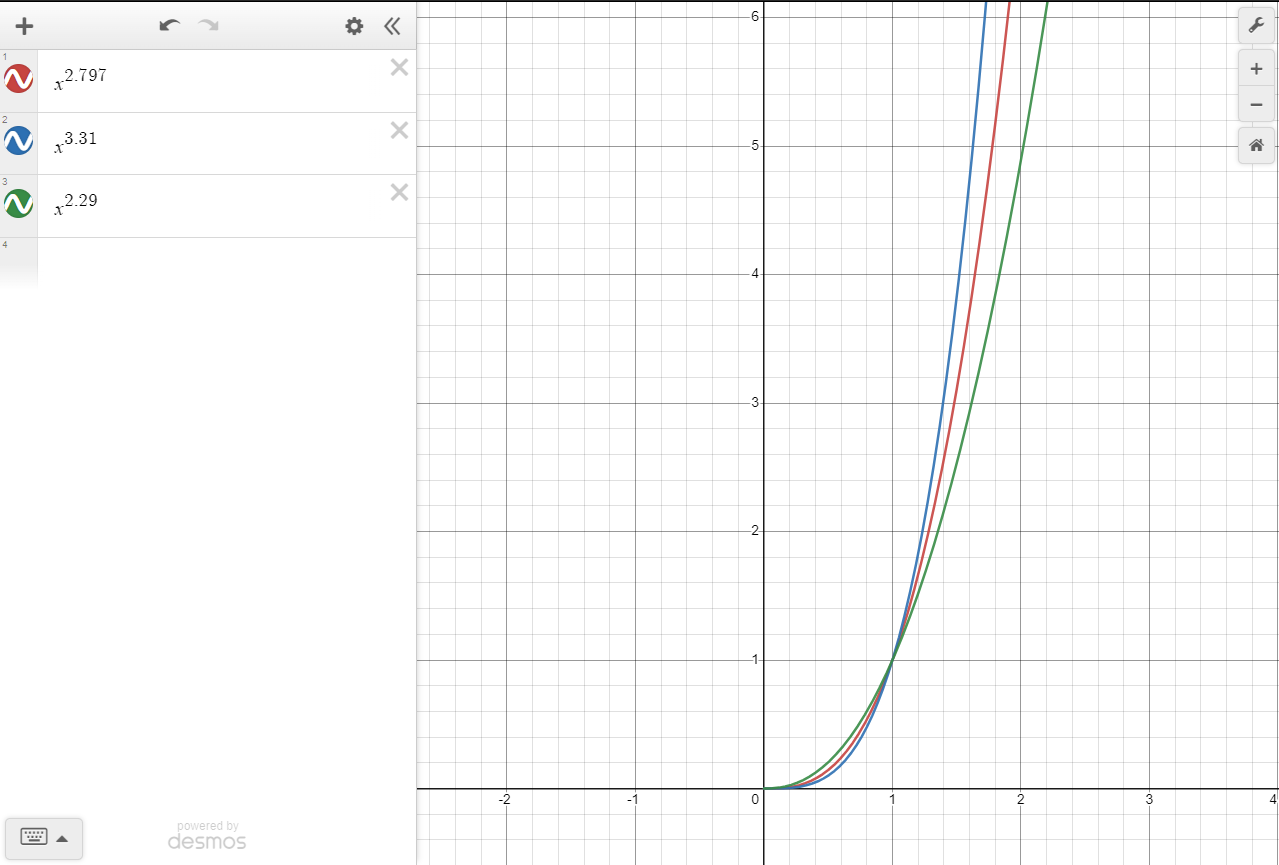
Example of the non-log function graphed using the derived power. $O(n^{2.8})$
This is in respects to time (ms). When accounting for just the growth of input, the input will grow in a polynomial fashion.
Math behind the calculations
A simplistic understanding how the time complexity is extracted stems from the log power rule.
Power Rule:
$log(n^k) = k \cdot log(n)$
After apply a log to both n and y variables, a linear regression is applied.
$y = time, n = input size, b = constant$
$log(y) = log(n^k) + b$
apply the power rule
$log(y) = k \cdot log(n) + b$
Everything can be ignored except for k. k determines the slope of line and tells us the time complexity.
$time complexity = N^k$
Jupyter Lab
The package can also be used in jupyter notebooks.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file TimeComplex-0.0.1.tar.gz.
File metadata
- Download URL: TimeComplex-0.0.1.tar.gz
- Upload date:
- Size: 5.7 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
ab50467f75b8e1ef21be775d01a9e510f3917b940b56457590a0fb38b2f813f5
|
|
| MD5 |
753219e6ce683369c6ed6df6e999f3e8
|
|
| BLAKE2b-256 |
af07d3023c58b9e9e410fc6359380557ba3537ab51475656fb68645b1841bafa
|