The ADER method for solving any (potentially very stiff) hyperbolic system of PDEs
Project description
A Python implementation of the ADER method for solving any (potentially very stiff) hyperbolic system of PDEs of the following form:
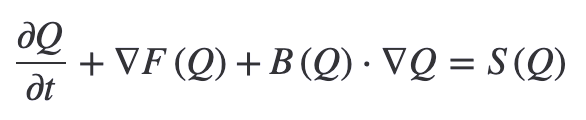
An arbitrary number of spatial domains can be used, and this implementation is capable of solving the equations to any order of accuracy. Second-order parabolic PDEs will be implemented soon.

Installation
Requires Python 3.6. Run pip install ader
The following dependencies will be installed:
NumPy 1.14.5
SciPy 1.1.0
Tangent 0.1.9
Background
Given cell-wise constant initial data defined on a computational grid, this program performs an arbitrary-order polynomial reconstruction of the data in each cell, according to a modified version of the WENO method, as presented in [1].
To the same order, a spatio-temporal polynomial reconstruction of the data is then obtained in each spacetime cell by the Discontinuous Galerkin method, using the WENO reconstruction as initial data at the start of the timestep (see [2,3]).
Finally, a finite volume update step is taken, using the DG reconstruction to calculate the values of the intercell fluxes and non-conservative intercell jump terms, and the interior source terms and non-conservative terms (see [3]).
The intercell fluxes and non-conservative jumps are calculated using either a Rusanov-type flux [4], a Roe-type flux [5], or an Osher-type flux [6].
Usage
Defining the System of Equations
The user must define the flux function (returning a NumPy array):
F(Q, d, model_params)
Given a vector of conserved variables Q, F must return the flux in direction d (where d=0,1,... corresponds to the x-,y-,… axes). model_params should be an object containing any other parameters required by the model in the calculation of the flux (for example, the heat capacity ratio in the Euler equations, or the viscosity in the Navier-Stokes equations). model_params does not have to be used, but it must be contained in the signature of F.
Similarly, if required, the nonconservative matrix B(Q) in direction d must be defined as a square NumPy array, thus:
B(Q, d, model_params)
If required, the source terms must be defined as a NumPy array thus:
S(Q, model_params)
Note that the governing system of PDEs can be written as:
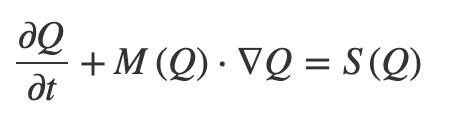
where the system Jacobian M corresponds to:
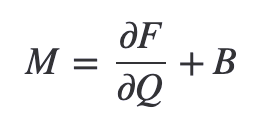
If an analytical form for M is known, it should be defined thus:
M(Q, d, model_params)
If an analytical form for the eigenvalue of M with the largest absolute value is known, it should be defined thus:
max_eig(Q, d, model_params)
The system Jacobian and largest absolute eigenvalue are required for the ADER method. If no analytical forms are available, they will be derived from the supplied flux (and nonconservative matrix, if supplied) using automatic differentiation. This will introduce some computational overhead, however, and some considerations need to be made when defining the flux function (see the dedicated section below).
Solving the Equations
Suppose we are solving the reactive Euler equations in 2D. We define F and S as above (but not B, as the equations are conservative). We also define model_params to hold the heat capacity ratio and reaction constants. These equations contain 5 conserved variables. To solve them to order 3, with 4 CPU cores, we set up the solver object thus:
from ader import Solver solver = Solver(nvar=5, ndim=2, F=F, B=None, S=S, model_params=model_params, order=3, ncore=4)
Analytical forms of the system Jacobian and the eigenvalue of largest absolute size exist for the reactive Euler equations. If we define these in M and max_eig we may instead create the solver object thus:
solver = Solver(nvar=5, ndim=2, F=F, B=None, S=S, M=M, max_eig=max_eig, model_params=model_params, order=3, ncore=4)
To solve a particular problem, we must define the initial state, initial_grid. This must be a NumPy array with 3 axes, such that initial_grid[i,j,k] is equal to the value of the kth conserved variable in cell (i,j). We must also define list dX=[dx,dy] where dx,dy are the grid spacing in the x and y axes. To solve the problem to a final time of 0.5, with a CFL number of 0.9, while printing all output, we call:
solution = solver.solve(initial_grid, 0.5, dX, cfl=0.9, verbose=True)
Advanced Usage
The Solver class has the following additional arguments:
riemann_solver (default ‘rusanov’): Which Riemann solver should be used. Options: ‘rusanov’, ‘roe’, ‘osher’.
stiff_dg (default False): Whether to use a Newton Method to solve the root finding involved in calculating the DG predictor.
stiff_dg_guess (default False): Whether to use an advanced initial guess for the DG predictor (only for very stiff systems).
newton_dg_guess (default False): Whether to compute the advanced initial guess using a Newton Method (only for very, very stiff systems).
DG_TOL (default 6e-6): The tolerance to which the DG predictor is calculated.
DG_MAX_ITER (default 50): Maximum number of iterations attempted if solving the DG root finding problem iteratively (not with a Newton Method)
WENO_r (default 8): The WENO exponent r.
WENO_λc (default 1e5): The WENO weighting of the central stencils.
WENO_λs (default 1): The WENO weighting of the side stencils.
WENO_ε (default 1e-14): The constant used in the WENO method to avoid numerical issues.
The Solver.solve method has the following additional arguments:
boundary_conditions (default ‘transitive’): Which kind of boundary conditions to use. Options: ‘transitive’, ‘periodic’, func(grid, N, ndim). In the latter case, the user defines a function with the stated signature. It should return a NumPy array with the same number of axes as grid, but with N more cells on either side of the grid in each spatial direction, where N is equal to the order of the method being used. These extra cells are required by an N-order method.
callback (default None): A user-defined callback function with signature callback(grid, t, count) where grid is the value of the computational grid at time t (and timestep count).
Examples
Check out example.py to see a couple of problems being solved for the GPR model and the reaction Euler equations.
Notes
Speed
This implementation is pretty slow. It’s really only intended to be used only for academic purposes. If you have a commercial application that requires a rapid, bullet-proof implementation of the ADER method or the GPR model, then get in touch (jackson.haran@gmail.com).
Automatic Differentiation
The automatic differentiation used to derive M and max_eig is performed using Google’s Tangent library. Although it’s great, this library is quite new, and it cannot cope with all operations that you may use in your fluxes (although development is proceeding quickly). In particular, it will never be able to handle closures, and classes are not yet implemented. Some NumPy functions such as inv have not yet been implemented. If you run into issues, drop me a quick message and I’ll let you know if I can make it work.
References
Dumbser, Zanotti, Hidalgo, Balsara - ADER-WENO finite volume schemes with space-time adaptive mesh refinement
Dumbser, Castro, Pares, Toro - ADER schemes on unstructured meshes for nonconservative hyperbolic systems: Applications to geophysical flows
Dumbser, Hidalgo, Zanotti - High order space-time adaptive ADER-WENO finite volume schemes for non-conservative hyperbolic systems
Toro - Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction
Dumbser, Toro - On Universal Osher-Type Schemes for General Nonlinear Hyperbolic Conservation Laws
Dumbser, Toro - A simple extension of the Osher Riemann solver to non-conservative hyperbolic systems
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file ader-1.2.1.tar.gz.
File metadata
- Download URL: ader-1.2.1.tar.gz
- Upload date:
- Size: 19.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.13.0 pkginfo/1.5.0.1 requests/2.22.0 setuptools/41.2.0 requests-toolbelt/0.9.1 tqdm/4.35.0 CPython/3.6.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
204576a968ba37b172e206bb3f3ce514b5fd05fc794b84528ba487b8d6a55d5e
|
|
| MD5 |
2c66e7dcea7dc5f51e5a79032940d5d5
|
|
| BLAKE2b-256 |
2f9edfc1397341e76b32618e24ce7fae694e7492102ef1fe5ae2b52a147f9b5a
|










