A Python implementation of the Bees Algorithm. This library allows an out-of-the-box use of the optimisation algorithm on an user-defined target function. The algorithm can be configured to find either the minimum or the maximum of the target function with an iterative process.
Project description
BeesAlgorithm - A Python Implementation
This repository contains a Bees Algorithm implementation in Python 3. For a more complete documentation please refer to the project page.
The aim is to make available to everyone an implementation, built with the minimal number of dependencies, which can be easily integrated in larger projects as well as used out-of-the-box to solve specific problems.
The Bees Algorithm is an intelligent optimization technique belonging to the swarm algorithms field. Given a parametric objective function, the goal of the algorithm is to find the parameter values that maximise/minimise the output of the objective function.
Many real-world problems can be modeled as the optimisation of a parametric objective function, therefore effective algorithms to handle this kind of problems are of primary importance in many fields. The Bees Algorithm performs simultaneus aggressive local searches around the most promising parameter settings of the objective function. The algorithm is proven to outperform other intelligent optimisation techniques in many benchmark functions[3][4][5] as well as real world problems.
On top of this Python version, implmentations of the bees Algorithm in C++ and Matlab are also available in the respective repositories.
The main steps of the Bees Algorithm will be described in the next section. For more information please refer to the official Bees Algorithm website and the wikipedia page. If you are interested in a detailed analysis of the algorithm, and the properties of its search strategy, please refer to this paper[1]:
- Luca Baronti, Marco Castellani, and Duc Truong Pham. "An Analysis of the Search Mechanisms of the Bees Algorithm." Swarm and Evolutionary Computation 59 (2020): 100746.
If you are using this implementation of the Bees Algorithm for your research, feel free to cite this work in your paper using the following BibTex entry:
@article{baronti2020analysis,
title={An Analysis of the Search Mechanisms of the Bees Algorithm},
author={Baronti, Luca and Castellani, Marco and Pham, Duc Truong},
journal={Swarm and Evolutionary Computation},
volume={59},
pages={100746},
year={2020},
publisher={Elsevier},
doi={10.1016/j.swevo.2020.100746},
url={https://doi.org/10.1016/j.swevo.2020.100746}
}
Installation
This module is available on pip and can be installed as follows:
$ pip3 install bees_algorithm
Introduction on the Bees Algorithm
The Bees Algorithm is a nature-inspired search method that mimics the foraging behaviour of honey bees. It was created by Prof. D.T. Pham and his co-workers in 2005[2], and described in its standard formulation by Pham and Castellani[3].
The algorithm uses a population of agents (artificial bees) to sample the solution space. A fraction of the population (scout bees) searches randomly for regions of high fitness (global search). The most successful scouts recruit a variable number of idle agents (forager bees) to search in the proximity of the fittest solutions (local search). Cycles of global and local search are repeated until an acceptable solution is discovered, or a given number of iterations have elapsed.
The standard version of the Bees Algorithm includes two heuristics: neighbourhood shrinking and site abandonment. Using neighbourhood shrinking the size of the local search is progressively reduced when local search stops progressing on a given site. The site abandonment procedure interrupts the search at one site after a given number of consecutive stagnation cycles, and restarts the local search at a randomly picked site.
The algorithm requires a number of parameters to be set, namely: the number of scout bees (ns), number of sites selected out of ns visited sites (nb), number of elite sites out of nb selected sites (ne), number of bees recruited for the best ne sites (nre), number of bees recruited for the other (nb-ne) selected sites (nrb). The heuristics also require the set of the initial size of the patches (ngh) and the number of cycles after which a site is abandoned (stlim). Finally, the stopping criterion must be defined.
The algorithm starts with the ns scout bees being placed randomly in the search space and the main algorithm steps can be summarised as follows:
- Evaluate the fitness of the population according the objective function;
- Select the best nb sites for neighbourhood (local) search;
- Recruit nrb forager bees for the selected sites (nre bees for the best ne sites) and evaluate their fitnesses;
- Select the fittest bee from each local site as the new site centre;
- If a site fails to improve in a single local search, its neighbourhood size is reduced (neighbourhood shrinking);
- If a site fails to improve for stlim cycles, the site is abandoned (site abandonment);
- Assign the remaining bees to search uniformly the whole search space and evaluate their fitnesses;
- If the stopping criterion is not met, return to step 2;
Usage
This repository offers two kinds of libraries. The library contained in bees_algorithm.py is a simple python implementation of the iterative Bees Algorithm. The libraries contained in bees_algorithm_parallel_algorithm.py and bees_algorithm_parallel_testing.py offer parallel versions of the algorithm, which is implemented on two different levels of parallelisms.
Guidelines
The implementations present here try to cover the following use cases:
- General use of the Bees Algorithm on a single test when only a limited number of iterations are expected: use BeesAlgorithm from bees_algorithm.py;
- Single test using a computationally expensive objective function, a large number of dimensions or iterations: use ParallelBeesAlgorithm from bees_algorithm_parallel_algorithm.py;
- Single test using an even more computationally expensive objective function, a larger number of dimensions or iterations: use FullyParallelBeesAlgorithm from bees_algorithm_parallel_algorithm.py;
- Multiple tests on the same objective function: use BeesAlgorithmTester from bees_algorithm_parallel_testing.py;
Please refer to the tests present in the following test section for the resons behind these guidelines.
Iterative Version
To use the library just import it
from bees_algorithm import BeesAlgorithm
then define your objective function (an hypesphere in this case)
def hypersphere(x):
return -sum([pow(xi,2) for xi in x])
and the search boundaries (in this case we are assuming a 4-dimensional search)
search_boundaries=([-5,-5,-5,-5], [5,5,5,5])
This implementation of the bees algorithm will always try to find the solution that maximize the objective function.
Therefore, if you have to find the minimum of your function $g(x)$ simply implement the objective function $f(x)=-g(x)$.
The next step is create an instance of the algoritm:
alg = BeesAlgorithm(hypersphere,search_boundaries[0],search_boundaries[1])
This will create an instance of the bees algorithm with default parameters (ns=10,nb=5,ne=1,nrb=10,nre=15,stlim=10,shrink_factor=.2). To use a different set of parameters, it's sufficient to pass the right values in the constructor like that:
alg = BeesAlgorithm(hypersphere,search_boundaries[0],search_boundaries[1],ns=0,nb=14,ne=1,nrb=5,nre=30,stlim=10)
This implementation of the bees algorithm use a simplified parameters formulation for the scout bees. Normally the parameter ns indicates the number of best sites and the number of scout bees used for the global search at each iteration. In this simpler formulation the parameter ns is the number of scout bees that are exclusively used for the global search, instead. Therefore setting ns=0 means that no scout bees are used for the global search.
In any case, it's possible to use the traditional parameters notation setting useSimplifiedParameters=True in the constructor.
To perform the optimisation is possible to do it iteratively calling:
alg.performSingleStep()
which perform a single iteration of the algoritm. Alternatively it's possible to perform the search all at once with:
alg.performFullOptimisation(max_iteration=5000)
In this case, two different stop criteria can be used: max_iteration wil interrupt the optimisation when a certain number of iterations are reached and max_score will interrupt it when a certain score is reached. If this method is used, at least one stop criterion must be specified. Finally, it is possible to use both the stop criteria, in which case the algorithm will stop when the first one is reached.
To assess the state of the algorithm, as well as the final result, the following variable can be accessed:
best = alg.best_solution
best.score # is the score of the best solution (e.g. 0.0 in our case)
best.values # are the coordinates of the best solution (e.g. [0.0, 0.0, 0.0, 0.0] in our case)
It is also possible to asses the score and values of all the current nb best sites accessing to the list alg.current_sites.
The variable best_solution contains the best solution found so far by the algorithm, which may or may not be included in the current best sites list current_sites.
Parallel Versions
The parallel version exposes the data structures and functions to run the Bees Algorithm in parallel on two different levels:
- At the testing level, where a certain number of instances of the iterative Bees Algorithm are run in parallel on the same objective function;
- At the algorithm level, where a single instance of a parallel version of the Bees Algorithm is run on a certain objective function;
Despite using a prallel version of the algorithm in a parallel may looks like a good idea, the eccessive prolification of processes that will result would most likely impact negatively on the performance. For this reason other kind of mixed parallelisms are not implemented here.
Parallel Version: Testing Level
Being a sthocastic algorithm, the final result of the Bees Algorithm is not deterministic. Therefore, running multiple instances of the algorithm on the same problem is useful to assess the general quality of the Bees Algorithm, or of a certain selection of its parameters, on a given problem.
In this case (testing level) it is possible to import:
from bees_algorithm import BeesAlgorithmTester
create an instance of the class BeesAlgorithmTester class similarly to how is done with the iterative version:
tester = BeesAlgorithmTester(hypersphere,search_boundaries[0],search_boundaries[2])
and finally call the run_tests function:
tester.run_tests(n_tests=50, max_iteration=5000)
which accepts the parameter n_tests, which defines how many test ought to be performed, the optional parameter verbose, useful to assess the completion of the single processes and the stop criteria used (similar to the performFullOptimisation function).
Optionallly, it is also possible to pass the argument n_processes to define the degree of parallelism (namely, how many processes are run at the same time). If it is not present, the number of cores of the CPU will be used as degree of parallelism. It is advisable to not use an high value for this argument, otherwise the performances may be negatively impacted.
Once the run_tests function is terminated the final results can be accessed using the results list of the instance, this way:
res = tester.results
each element of the results list is a tuple (iteration, best_solution) representing the iteration reached and the best solution found for a run.
Parallel Version: Algorithm Level
Some characteristics of the Bees Algorithm pose serious limitation on the design of an effective parallel version. One of the most effective way to perform the algorithm in parallel is to run the sequence of sites local searches simultaneously. However, mapping a site search search on a thread/process that perform the whole site search (up to the point the site is abandoned) can't be entirerly done due to some info that need to be shared between the sites. For instance, at each iteration the algorithm must know:
- which nb sites are the best ones, to promote them to elite sites and give them more foragers;
- which nb sites need to be replaced by better solutions found in the global search (ns);
- how many local searches have been done so far, and what's the best solution, to assess the stop criteria;
To assess all these information, the parallel searches must stop-and-report to a central controller, reducing the parallelism performances greately. Removing heuristics like the elite sites, the global scouts, and accepting some approximation on the stop criteria (i.e. updating the number of iterations and best score only when a site is abandoned) will remove this problem. However these modifications will lead to a quite different algorithm than the standard one, so the two different approaches are implemented in this library.
Parallel Version: Algorithm Level - Partial
In this version, the Bees Algorithm works in parallel only in performing a single local search for all the sites.
That is, at each iteration, the nb sites perform a single local search in parallel. In this way it's possible to control the other aspects of the algorithm keeping its original behaviour and, at the same time, have an improvment in the completion time to a certain extent.
To use this parallel version of the Bees Algorithm it is possible to import:
from bees_algorithm import ParallelBeesAlgorithm
and create an instance of the class ParallelBeesAlgorithm class exactly how is done with the iterative version:
alg = ParallelBeesAlgorithm(hypersphere,search_boundaries[0],search_boundaries[2])
where the constructors takes all the parameters of the iterative version, with the addition of the n_processes parameters, set as the number of cores of the current machine as default. The algorithm instance can then be used exactly the same way as the iterative case.
Parallel Version: Algorithm Level - Full
In this version, nb sites perform separate searches in a higher degree of parallelism.
Under ideal circumnstances, nb threads are run in parallel, each one performing a search for a site. When the site is abandoned, the associated thread will generate a new site and start a new search. Threads communicate to eachothers only in assessing the stop criteria, mostly when a site is abandoned. This will avoid overhead induced by accessing to shared resources with high frequency.
This version can potentially offers an higher performance Bees Algorithm, however it comes with the following limitations:
- No elite sites can be used;
- No global scouts can be used;
- The value of the final number of iterations may not be accurate (can be overestimed);
To use this parallel version of the Bees Algorithm it is possible to import the same file:
from bees_algorithm import FullyParallelBeesAlgorithm
and create an instance of the class FullyParallelBeesAlgorithm class similarry as it is done with the iterative version:
alg = FullyParallelBeesAlgorithm(hypersphere,search_boundaries[0],search_boundaries[2])
The key difference is that the constructor accept the following parameters: score_function, range_min, range_max, nb, nrb, stlim, initial_ngh, shrink_factor,useSimplifiedParameters and n_processes.
The number of threads used in this case will be:
\min(nb, n\_processes)
The algorithm instance can then be used exactly the same way as the iterative case.
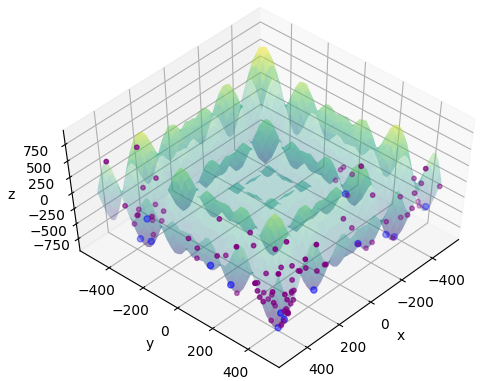
Step-by-step Visualisation
A function that plot a visual rapresentation of the Bees Algorithm steps is included in this package. The function visualize_iteration_steps can be called in lieu of performFullOptimisation. It accepts no parameters.
Here is an example using the Schwefel target function (see section below for details):
import benchmark_functions as bf
b_func = bf.Schwefel(opposite=True)
suggested_lowerbound, suggested_upperbound = b_func.suggested_bounds()
schwefel_bees_parameters = {'ns':0, 'nb':14, 'ne':1, 'nrb':5, 'nre':30, 'stlim':10}
alg = BeesAlgorithm(b_func,
suggested_lowerbound, suggested_upperbound,
**schwefel_bees_parameters)
alg.visualize_iteration_steps()
References
- [1]: Luca Baronti, Marco Castellani, and Duc Truong Pham. "An Analysis of the Search Mechanisms of the Bees Algorithm." Swarm and Evolutionary Computation 59 (2020): 100746.
- [2]: Pham, Duc Truong, et al. "The Bees Algorithm—A Novel Tool for Complex Optimisation Problems." Intelligent production machines and systems. 2006. 454-459.
- [3]: Pham, Duc Truong, and Marco Castellani. "The bees algorithm: modelling foraging behaviour to solve continuous optimization problems." Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 223.12 (2009): 2919-2938.
- [4]: Pham, Duc Truong, and Marco Castellani. "Benchmarking and comparison of nature-inspired population-based continuous optimisation algorithms." Soft Computing 18.5 (2014): 871-903.
- [5]: Pham, Duc Truong, and Marco Castellani. "A comparative study of the Bees Algorithm as a tool for function optimisation." Cogent Engineering 2.1 (2015): 1091540.
For more references please refer to the README file in the C++ repository.
Author and License
This library is developed and mantained by Luca Baronti (gmail address: lbaronti) and released under GPL v3 license.
Versions History
v1.0.2
- minor fixes
- minor code refactoring
- added numpy dependnency
- moved static method visualize_steps to instance method visualize_iteration_steps
v1.0.1
- minor fixes in the README
v1.0.0
- full stable release
- added unit tests
- made compliant with benchmark_functions v1.1.3
v0.1.1
- initial beta release
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file bees_algorithm-1.0.2.tar.gz.
File metadata
- Download URL: bees_algorithm-1.0.2.tar.gz
- Upload date:
- Size: 35.1 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.8.0 colorama/0.4.4 importlib-metadata/4.6.4 keyring/23.5.0 pkginfo/1.8.2 readme-renderer/34.0 requests-toolbelt/0.9.1 requests/2.25.1 rfc3986/1.5.0 tqdm/4.57.0 urllib3/1.26.5 CPython/3.10.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
4e1813899eb74c119a9ffbb993b6e0ba5e830ba0115a51ae4376b90d16e0f95b
|
|
| MD5 |
fc24e0f51b0b58dcbaf179d36b84b2fd
|
|
| BLAKE2b-256 |
40b9e5b3c2c7499c86a968a22eb888c6219d8b2cb76ad1509eab9066b72fb1f0
|
File details
Details for the file bees_algorithm-1.0.2-py3-none-any.whl.
File metadata
- Download URL: bees_algorithm-1.0.2-py3-none-any.whl
- Upload date:
- Size: 27.1 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.8.0 colorama/0.4.4 importlib-metadata/4.6.4 keyring/23.5.0 pkginfo/1.8.2 readme-renderer/34.0 requests-toolbelt/0.9.1 requests/2.25.1 rfc3986/1.5.0 tqdm/4.57.0 urllib3/1.26.5 CPython/3.10.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a0570ca90d7f44076a4152c893d54f833ec86c97220cb50c96a636034e098a98
|
|
| MD5 |
eeb6720ba28da0019010661c53b3b246
|
|
| BLAKE2b-256 |
d2b89595307e7542ff9dbdb6423bf81f49b6e9e4fd67fb7456abbb970a5bc413
|