Formal Concept Analysis with Python
Project description
Concepts is a simple Python implementation of Formal Concept Analysis (FCA).
FCA provides a mathematical model for describing a set of objects (e.g. King Arthur, Sir Robin, and the holy grail) with a set of properties (e.g. human, knight, king, and mysterious) which each of the objects either has or not. A table called formal context defines which objects have a given property and vice versa which properties a given object has.
Installation
This package runs under Python 2.7 and 3.3+, use pip to install:
$ pip install conceptsThis will also install the bitsets and graphviz packages from PyPI as required dependencies.
Rendering lattice graphs depends on the Graphviz software. Make sure its dot executable is on your systems’ path.
Formal contexts
With Concepts, formal contexts can be created from a string with an ASCII-art style cross-table. The objects and properties will simply be represented by strings. Separate the property columns with pipe symbols (|), create one row for each objects, one column for each property, and indicate the presence of a property with the character X.
Note that the object and property names need to be disjoint to uniquely identify them.
>>> from concepts import Context
>>> c = Context.fromstring('''
... |human|knight|king |mysterious|
... King Arthur| X | X | X | |
... Sir Robin | X | X | | |
... holy grail | | | | X |
... ''')
>>> c # doctest: +ELLIPSIS
<Context object mapping 3 objects to 4 properties at 0x...>You can also load contexts from files in different plain-text formats, see below.
After creation, the parsed content of the table is available on the context object.
>>> c.objects # row headings
('King Arthur', 'Sir Robin', 'holy grail')
>>> c.properties # column headings
('human', 'knight', 'king', 'mysterious')
>>> c.bools # data cells
[(True, True, True, False), (True, True, False, False), (False, False, False, True)]The context object can be queried to return the common properties for a collection of objects (common intent, intension) as well as the common objects for a collection of properties (common extent, extension):
>>> c.intension(['King Arthur', 'Sir Robin']) # common properties?
('human', 'knight')
>>> c.extension(['knight', 'mysterious']) # objects with these properties?
()In FCA these operations are called derivations and usually notated with the prime symbol(‘).
>>> c.extension(['knight', 'king'])
('King Arthur',)
>>> c.extension(['mysterious', 'human'])
()Formal concepts
A pair of objects and properties such that the objects share exactly the properties and the properties apply to exactly the objects is called formal concept. Informally, they result from maximal rectangles of X-marks in the context table, when rows and columns can be reordered freely.
You can retrieve the closest matching concept corresponding to a collection of objects or properties with the __getitem__ method of the concept object:
>>> c[('king',)] # closest concept matching intent/extent
(('King Arthur',), ('human', 'knight', 'king'))
>>> assert c.intension(('King Arthur',)) == ('human', 'knight', 'king')
>>> assert c.extension(('human', 'knight', 'king')) == ('King Arthur',)
>>> c[('King Arthur', 'Sir Robin')]
(('King Arthur', 'Sir Robin'), ('human', 'knight'))Within each context, there is a maximally general concept comprising all of the objects as extent and having an empty intent (supremum).
>>> c[('Sir Robin', 'holy grail')] # maximal concept, supremum
(('King Arthur', 'Sir Robin', 'holy grail'), ())Furthermore there is a minimally general concept comprising no object at all and having all properties as intent (infimum).
>>> c[('mysterious', 'knight')] # minimal concept, infimum
((), ('human', 'knight', 'king', 'mysterious'))The concepts of a context can be ordered by extent set-inclusion (or dually intent set-inclusion). With this (partial) order, they form a concept lattice having the supremum concept (i.e. the tautology) at the top, the infimum concept (i.e. the contradiction) at the bottom, and the other concepts in between.
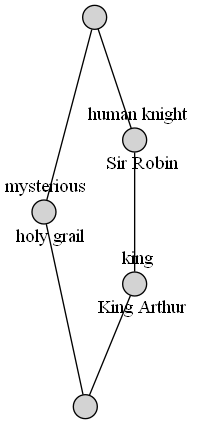
Concept lattice
The concept lattice of a context contains all pairs of objects and properties (formal concepts) that can be retrieved from a formal context:
>>> c # doctest: +ELLIPSIS
<Context object mapping 3 objects to 4 properties at 0x...>
>>> l = c.lattice
>>> l # doctest: +ELLIPSIS
<Lattice object of 2 atoms 5 concepts 2 coatoms at 0x...>
>>> for extent, intent in l:
... print('%r %r' % (extent, intent))
() ('human', 'knight', 'king', 'mysterious')
('King Arthur',) ('human', 'knight', 'king')
('holy grail',) ('mysterious',)
('King Arthur', 'Sir Robin') ('human', 'knight')
('King Arthur', 'Sir Robin', 'holy grail') ()Individual concepts can be retrieved by different means :
>>> l.infimum # first concept, index 0
<Infimum {} <-> [human knight king mysterious]>
>>> l.supremum # last concept
<Supremum {King Arthur, Sir Robin, holy grail} <-> []>
>>> l[1]
<Atom {King Arthur} <-> [human knight king] <=> King Arthur <=> king>
>>> l[('mysterious',)]
<Atom {holy grail} <-> [mysterious] <=> holy grail <=> mysterious>The concepts form a directed acyclic graph and are linked upward (more general concepts, superconcepts) and downward (less general concepts, subconcepts):
>>> l.infimum.upper_neighbors # doctest: +NORMALIZE_WHITESPACE
(<Atom {King Arthur} <-> [human knight king] <=> King Arthur <=> king>,
<Atom {holy grail} <-> [mysterious] <=> holy grail <=> mysterious>)
>>> l[1].lower_neighbors
(<Infimum {} <-> [human knight king mysterious]>,)Visualization
To visualize the lattice, use its graphviz method:
>>> dot = l.graphviz()
>>> print(dot.source) # doctest: +ELLIPSIS, +NORMALIZE_WHITESPACE
// <Lattice object of 2 atoms 5 concepts 2 coatoms at 0x...>
digraph Lattice {
node [label="" shape=circle style=filled width=.25]
edge [dir=none labeldistance=1.5 minlen=2]
c0
c1
c1 -> c1 [color=transparent headlabel="King Arthur" labelangle=270]
c1 -> c1 [color=transparent labelangle=90 taillabel=king]
c1 -> c0
c2
c2 -> c2 [color=transparent headlabel="holy grail" labelangle=270]
c2 -> c2 [color=transparent labelangle=90 taillabel=mysterious]
c2 -> c0
c3
c3 -> c3 [color=transparent headlabel="Sir Robin" labelangle=270]
c3 -> c3 [color=transparent labelangle=90 taillabel="human knight"]
c3 -> c1
c4
c4 -> c2
c4 -> c3
}
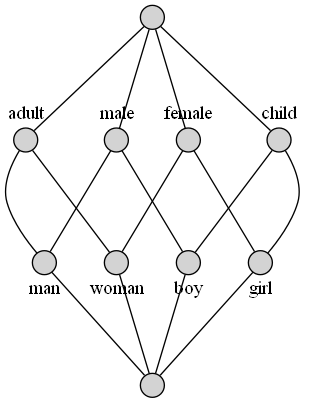
For example:
>>> h = Context.fromstring('''
... |male|female|adult|child|
... man | X | | X | |
... woman| | X | X | |
... boy | X | | | X |
... girl | | X | | X |
... ''')
>>> dot = h.lattice.graphviz()
>>> print(dot.source) # doctest: +ELLIPSIS, +NORMALIZE_WHITESPACE
// <Lattice object of 4 atoms 10 concepts 4 coatoms at 0x...>
digraph Lattice {
node [label="" shape=circle style=filled width=.25]
edge [dir=none labeldistance=1.5 minlen=2]
c0
c1
c1 -> c1 [color=transparent headlabel=man labelangle=270]
c1 -> c0
c2
c2 -> c2 [color=transparent headlabel=woman labelangle=270]
c2 -> c0
c3
c3 -> c3 [color=transparent headlabel=boy labelangle=270]
c3 -> c0
...
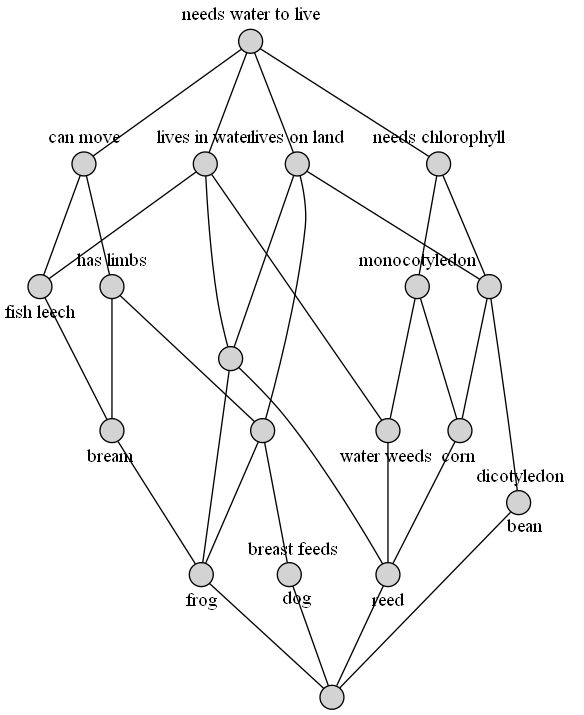
A more complex example:
>>> w = Context.fromfile('examples/liveinwater.cxt')
>>> dot = w.lattice.graphviz()
>>> print(dot.source) # doctest: +ELLIPSIS, +NORMALIZE_WHITESPACE
// <Lattice object of 4 atoms 19 concepts 4 coatoms at 0x...>
digraph Lattice {
node [label="" shape=circle style=filled width=.25]
edge [dir=none labeldistance=1.5 minlen=2]
c0
c1
c1 -> c1 [color=transparent headlabel=frog labelangle=270]
c1 -> c0
c2
c2 -> c2 [color=transparent headlabel=dog labelangle=270]
c2 -> c2 [color=transparent labelangle=90 taillabel="breast feeds"]
c2 -> c0
c3
c3 -> c3 [color=transparent headlabel=reed labelangle=270]
c3 -> c0
...
For details on the resulting objects interface, check the documentation of this package.
Persistence
Contexts can be loaded from and saved to files in CXT, CSV, and ASCII-art table format:
>>> c1 = Context.fromfile('examples/liveinwater.cxt')
>>> c1 # doctest: +ELLIPSIS
<Context object mapping 8 objects to 9 properties at 0x...>
>>> c2 = Context.fromfile('examples/liveinwater.csv', frmat='csv')
>>> c2 # doctest: +ELLIPSIS
<Context object mapping 8 objects to 9 properties at 0x...>
>>> c3 = Context.fromfile('examples/liveinwater.txt', frmat='table')
>>> c3 # doctest: +ELLIPSIS
<Context object mapping 8 objects to 9 properties at 0x...>
>>> c1 == c2 == c3
TrueContext objects are pickleable:
>>> import pickle
>>> pickle.loads(pickle.dumps(c)) == c
TrueFurther reading
The generation of the concept lattice is based on the algorithm from C. Lindig. Fast Concept Analysis. In Gerhard Stumme, editors, Working with Conceptual Structures - Contributions to ICCS 2000, Shaker Verlag, Aachen, Germany, 2000.
The included example CXT files are taken from Uta Priss’ FCA homepage
See also
The implementation is based on these Python packages:
The following package is build on top of concepts:
features – Feature set algebra for linguistics
If you want to apply FCA to bigger data sets, you might want to consider other implementations based on more sophisticated algorithms like In-Close or Fcbo.
License
Concepts is distributed under the MIT license.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Hashes for concepts-0.7.3-py2.py3-none-any.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 07ad9b5f3f02e7368856312324c1e5b89f03134bc7426858253768a4dc21f551 |
|
| MD5 | ce29474ac0161a7178718fdefaa53d61 |
|
| BLAKE2b-256 | b9d2831eecb25f3f496be5ca4ef273c6975580fca7a9daf1fc646bbfedc32c89 |
















