Distance measures for time series (Dynamic Time Warping, fast C implementation)
Project description
Time Series Distances
Library for time series distances (e.g. Dynamic Time Warping) used in the DTAI Research Group. The library offers a pure Python implementation and a fast implementation in C. The C implementation has only Cython as a dependency. It is compatible with Numpy and Pandas and implemented such that unnecessary data copy operations are avoided.
Documentation: http://dtaidistance.readthedocs.io
Example:
from dtaidistance import dtw
import numpy as np
s1 = np.array([0.0, 0, 1, 2, 1, 0, 1, 0, 0])
s2 = np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0])
d = dtw.distance_fast(s1, s2)
Citing this work:
Wannes Meert, Kilian Hendrickx, Toon Van Craenendonck, Pieter Robberechts, Hendrik Blockeel & Jesse Davis.
DTAIDistance (Version v2). Zenodo.
http://doi.org/10.5281/zenodo.5901139
New in v2:
- Numpy is now an optional dependency, also to compile the C library (only Cython is required).
- Small optimizations throughout the C code to improve speed.
- The consistent use of
ssize_tinstead ofintallows for larger data structures on 64 bit machines and be more compatible with Numpy. - The parallelization is now implemented directly in C (included if OpenMP is installed).
- The
max_distargument turned out to be similar to Silva and Batista's work on PrunedDTW [7]. The toolbox now implements a version that is equal to PrunedDTW since it prunes more partial distances. Additionally, ause_pruningargument is added to automatically setmax_distto the Euclidean distance, as suggested by Silva and Batista, to speed up the computation (a new methodub_euclideanis available). - Support in the C library for multi-dimensional sequences in the
dtaidistance.dtw_ndimpackage. - DTW Barycenter Averaging for clustering (v2.2).
- Subsequence search and local concurrences (v2.3).
- Support for N-dimensional time series (v2.3.7).
Installation
$ pip install dtaidistance
or
$ conda install -c conda-forge dtaidistance
The pip installation requires Numpy as a dependency to compile Numpy-compatible C code (using Cython). However, this dependency is optional and can be removed.
The source code is available at github.com/wannesm/dtaidistance.
If you encounter any problems during compilation (e.g. the C-based implementation or OpenMP is not available), see the documentation for more options.
Usage
Dynamic Time Warping (DTW) Distance Measure
from dtaidistance import dtw
from dtaidistance import dtw_visualisation as dtwvis
import numpy as np
s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
path = dtw.warping_path(s1, s2)
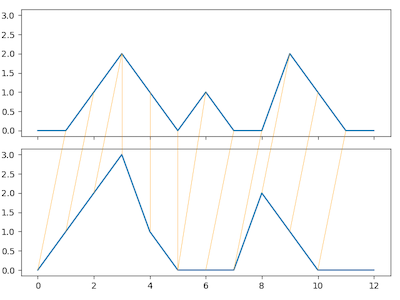
dtwvis.plot_warping(s1, s2, path, filename="warp.png")
DTW Distance Measure Between Two Series
Only the distance measure based on two sequences of numbers:
from dtaidistance import dtw
s1 = [0, 0, 1, 2, 1, 0, 1, 0, 0]
s2 = [0, 1, 2, 0, 0, 0, 0, 0, 0]
distance = dtw.distance(s1, s2)
print(distance)
The fastest version (30-300 times) uses c directly but requires an array as input (with the double type),
and (optionally) also prunes computations by setting max_dist to the Euclidean upper bound:
from dtaidistance import dtw
import array
s1 = array.array('d',[0, 0, 1, 2, 1, 0, 1, 0, 0])
s2 = array.array('d',[0, 1, 2, 0, 0, 0, 0, 0, 0])
d = dtw.distance_fast(s1, s2, use_pruning=True)
Or you can use a numpy array (with dtype double or float):
from dtaidistance import dtw
import numpy as np
s1 = np.array([0, 0, 1, 2, 1, 0, 1, 0, 0], dtype=np.double)
s2 = np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0])
d = dtw.distance_fast(s1, s2, use_pruning=True)
Check the __doc__ for information about the available arguments:
print(dtw.distance.__doc__)
A number of options are foreseen to early stop some paths the dynamic programming algorithm is exploring or tune the distance measure computation:
window: Only allow for shifts up to this amount away from the two diagonals.max_dist: Stop if the returned distance measure will be larger than this value.max_step: Do not allow steps larger than this value.max_length_diff: Return infinity if difference in length of two series is larger.penalty: Penalty to add if compression or expansion is applied (on top of the distance).psi: Psi relaxation to ignore begin and/or end of sequences (for cylical sequences) [2].use_pruning: Prune computations based on the Euclidean upper bound.
DTW Distance Measure all warping paths
If, next to the distance, you also want the full matrix to see all possible warping paths:
from dtaidistance import dtw
s1 = [0, 0, 1, 2, 1, 0, 1, 0, 0]
s2 = [0, 1, 2, 0, 0, 0, 0, 0, 0]
distance, paths = dtw.warping_paths(s1, s2)
print(distance)
print(paths)
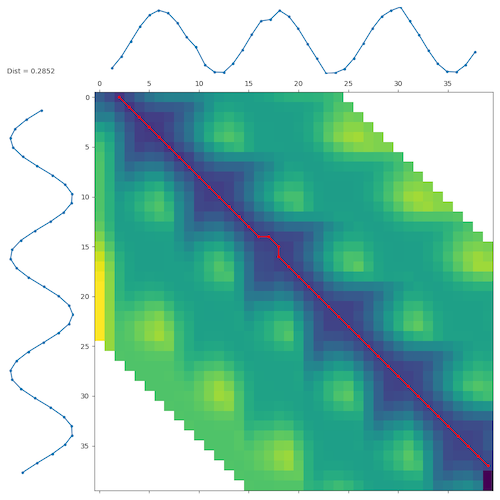
The matrix with all warping paths can be visualised as follows:
from dtaidistance import dtw
from dtaidistance import dtw_visualisation as dtwvis
import random
import numpy as np
x = np.arange(0, 20, .5)
s1 = np.sin(x)
s2 = np.sin(x - 1)
random.seed(1)
for idx in range(len(s2)):
if random.random() < 0.05:
s2[idx] += (random.random() - 0.5) / 2
d, paths = dtw.warping_paths(s1, s2, window=25, psi=2)
best_path = dtw.best_path(paths)
dtwvis.plot_warpingpaths(s1, s2, paths, best_path)
Notice the psi parameter that relaxes the matching at the beginning and end.
In this example this results in a perfect match even though the sine waves are slightly shifted.
DTW Distance Measures Between Set of Series
To compute the DTW distance measures between all sequences in a list of sequences, use the method dtw.distance_matrix.
You can set variables to use more or less c code (use_c and use_nogil) and parallel or serial execution
(parallel).
The distance_matrix method expects a list of lists/arrays:
from dtaidistance import dtw
import numpy as np
series = [
np.array([0, 0, 1, 2, 1, 0, 1, 0, 0], dtype=np.double),
np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0]),
np.array([0.0, 0, 1, 2, 1, 0, 0, 0])]
ds = dtw.distance_matrix_fast(series)
or a matrix (in case all series have the same length):
from dtaidistance import dtw
import numpy as np
series = np.matrix([
[0.0, 0, 1, 2, 1, 0, 1, 0, 0],
[0.0, 1, 2, 0, 0, 0, 0, 0, 0],
[0.0, 0, 1, 2, 1, 0, 0, 0, 0]])
ds = dtw.distance_matrix_fast(series)
DTW Distance Measures Between Set of Series, limited to block
You can instruct the computation to only fill part of the distance measures matrix. For example to distribute the computations over multiple nodes, or to only compare source series to target series.
from dtaidistance import dtw
import numpy as np
series = np.matrix([
[0., 0, 1, 2, 1, 0, 1, 0, 0],
[0., 1, 2, 0, 0, 0, 0, 0, 0],
[1., 2, 0, 0, 0, 0, 0, 1, 1],
[0., 0, 1, 2, 1, 0, 1, 0, 0],
[0., 1, 2, 0, 0, 0, 0, 0, 0],
[1., 2, 0, 0, 0, 0, 0, 1, 1]])
ds = dtw.distance_matrix_fast(series, block=((1, 4), (3, 5)))
The output in this case will be:
# 0 1 2 3 4 5
[[ inf inf inf inf inf inf] # 0
[ inf inf inf 1.4142 0.0000 inf] # 1
[ inf inf inf 2.2360 1.7320 inf] # 2
[ inf inf inf inf 1.4142 inf] # 3
[ inf inf inf inf inf inf] # 4
[ inf inf inf inf inf inf]] # 5
Clustering
A distance matrix can be used for time series clustering. You can use existing methods such as
scipy.cluster.hierarchy.linkage or one of two included clustering methods (the latter is a
wrapper for the SciPy linkage method).
from dtaidistance import clustering
# Custom Hierarchical clustering
model1 = clustering.Hierarchical(dtw.distance_matrix_fast, {})
cluster_idx = model1.fit(series)
# Augment Hierarchical object to keep track of the full tree
model2 = clustering.HierarchicalTree(model1)
cluster_idx = model2.fit(series)
# SciPy linkage clustering
model3 = clustering.LinkageTree(dtw.distance_matrix_fast, {})
cluster_idx = model3.fit(series)
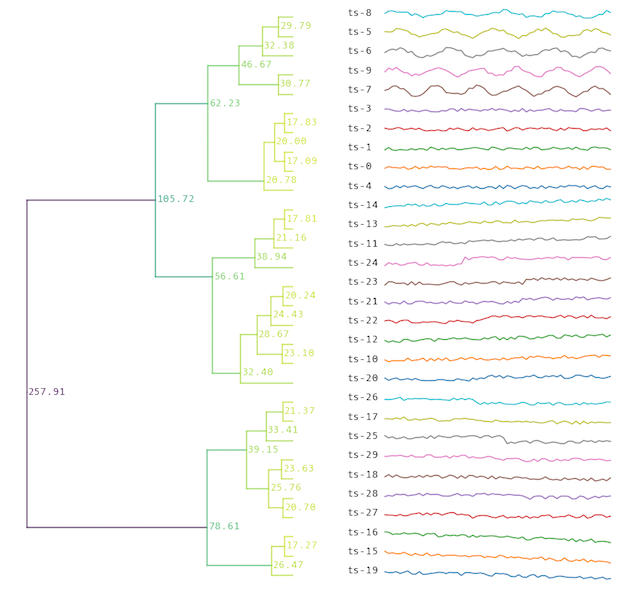
For models that keep track of the full clustering tree (HierarchicalTree or LinkageTree), the
tree can be visualised:
model.plot("myplot.png")
Dependencies
Optional:
Development:
Contact
References
- T. K. Vintsyuk, Speech discrimination by dynamic programming. Kibernetika, 4:81–88, 1968.
- H. Sakoe and S. Chiba, Dynamic programming algorithm optimization for spoken word recognition. IEEE Transactions on Acoustics, Speech and Signal Processing, 26(1):43–49, 1978.
- C. S. Myers and L. R. Rabiner, A comparative study of several dynamic time-warping algorithms for connected-word recognition. The Bell System Technical Journal, 60(7):1389–1409, Sept 1981.
- Mueen, A and Keogh, E, Extracting Optimal Performance from Dynamic Time Warping, Tutorial, KDD 2016
- D. F. Silva, G. E. A. P. A. Batista, and E. Keogh. On the effect of endpoints on dynamic time warping, In SIGKDD Workshop on Mining and Learning from Time Series, II. Association for Computing Machinery-ACM, 2016.
- C. Yanping, K. Eamonn, H. Bing, B. Nurjahan, B. Anthony, M. Abdullah and B. Gustavo. The UCR Time Series Classification Archive, 2015.
- D. F. Silva and G. E. Batista. Speeding up all-pairwise dynamic time warping matrix calculation, In Proceedings of the 2016 SIAM International Conference on Data Mining, pages 837–845. SIAM, 2016.
License
DTAI distance code.
Copyright 2016-2022 KU Leuven, DTAI Research Group
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distributions
File details
Details for the file dtaidistance-2.3.13.tar.gz.
File metadata
- Download URL: dtaidistance-2.3.13.tar.gz
- Upload date:
- Size: 985.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
b0344a9b6f642863fcedacf5de86c4a0a0d4b4adec9b9be561a6f513ecf5e695
|
|
| MD5 |
0393f8850b46e87d4fc3fa895dc80568
|
|
| BLAKE2b-256 |
320d04de7998fba3b4881bf9abb4abe4a5422a53050670000ea7f03abaf9d7ed
|
File details
Details for the file dtaidistance-2.3.13-cp312-cp312-win_amd64.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp312-cp312-win_amd64.whl
- Upload date:
- Size: 1.0 MB
- Tags: CPython 3.12, Windows x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
465f45d380a1cd4416201a9aeffa9fdf34848db10fe66918456d616989d61316
|
|
| MD5 |
f585cd6dc245c354062e189d3c3d7ae7
|
|
| BLAKE2b-256 |
bf9eb81d1db49a492dbd79eef25b852651b74c519af5fa081b7b2947275ae2ba
|
File details
Details for the file dtaidistance-2.3.13-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 3.0 MB
- Tags: CPython 3.12, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
d071392388dab99462922df8e4fb99f905e59888bd7246dee318ba7fe0d6332d
|
|
| MD5 |
90af60afcf0751238f9c513f4b9509cc
|
|
| BLAKE2b-256 |
d5705c8994a7d1408b89ca8b66773e7f005482013da5cb49816a7bc381d7faf7
|
File details
Details for the file dtaidistance-2.3.13-cp312-cp312-macosx_10_13_universal2.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp312-cp312-macosx_10_13_universal2.whl
- Upload date:
- Size: 1.5 MB
- Tags: CPython 3.12, macOS 10.13+ universal2 (ARM64, x86-64)
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a09b9916f8ecbf11ef3f8824bfb306c1c3bfc63a32dcb4703551a1d5bbe6fa6c
|
|
| MD5 |
04111a2b36a6c2db9d8f80c06960e8d4
|
|
| BLAKE2b-256 |
715e95d32583d7f0a76ece94177724465d4f4547e078c48c6588c06d40bf16bf
|
File details
Details for the file dtaidistance-2.3.13-cp311-cp311-win_amd64.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp311-cp311-win_amd64.whl
- Upload date:
- Size: 1.0 MB
- Tags: CPython 3.11, Windows x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
ac8536147977419a2ab5b4a89d97d91bbaf8ea339d91bbb63e26bea0a842ec5e
|
|
| MD5 |
6618cf52936aa757d63952a3cc201236
|
|
| BLAKE2b-256 |
81c9a1964a5aa966e20220a316c715d5b5ee55a874424336f7e992db76148c4d
|
File details
Details for the file dtaidistance-2.3.13-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 3.0 MB
- Tags: CPython 3.11, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
c61ef66588cac8b1f2ec7c8a7ca15bc6ae058804f8e5514919a0b682818fa60a
|
|
| MD5 |
c164f9c58064a4f40b7d0e46a557f49f
|
|
| BLAKE2b-256 |
50bd18e647e214865cfc37d95d3bd414240e83be31c3ad7354ea72949452cbfb
|
File details
Details for the file dtaidistance-2.3.13-cp311-cp311-macosx_10_9_universal2.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp311-cp311-macosx_10_9_universal2.whl
- Upload date:
- Size: 1.5 MB
- Tags: CPython 3.11, macOS 10.9+ universal2 (ARM64, x86-64)
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
02f2de97f147cd17c7de1b19140d3a5f48d876c19ae28105c12cca45f9af2520
|
|
| MD5 |
d4bfbeadabc321dd814e0c90e5568893
|
|
| BLAKE2b-256 |
10c0e690152c04207972cd6686553099ed7c81e5a658122e81787e6be8de8c2a
|
File details
Details for the file dtaidistance-2.3.13-cp310-cp310-win_amd64.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp310-cp310-win_amd64.whl
- Upload date:
- Size: 1.0 MB
- Tags: CPython 3.10, Windows x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
81527c52c8ba44b7756e3815646584c44c4f7277ef17ae98542d5a256bee462b
|
|
| MD5 |
b59997942b51a33620a970689ba49953
|
|
| BLAKE2b-256 |
503492077a69dc590e7cced9e3b8d43369eee22855f60919eccdd1562b3d7e39
|
File details
Details for the file dtaidistance-2.3.13-cp310-cp310-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp310-cp310-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 2.9 MB
- Tags: CPython 3.10, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
0f700efc7bf4c4ff6a13392816c0d50e3ca768f9da4868e3af4d09d38360a1c1
|
|
| MD5 |
4023b1ee2c6645036fbe8d4f82c37775
|
|
| BLAKE2b-256 |
f14bfdbe9551dc246fb4e97262934051f3788f8f2f21872a097bc27b52fa62cb
|
File details
Details for the file dtaidistance-2.3.13-cp310-cp310-macosx_10_9_universal2.whl.
File metadata
- Download URL: dtaidistance-2.3.13-cp310-cp310-macosx_10_9_universal2.whl
- Upload date:
- Size: 1.5 MB
- Tags: CPython 3.10, macOS 10.9+ universal2 (ARM64, x86-64)
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
b6a805736778afeb62966ff5dfd78e4f9c6d29667699ba91e3f69d2f2ecadf0e
|
|
| MD5 |
ed7149cb9771ed6b98ce525e2ff3b91e
|
|
| BLAKE2b-256 |
b4dbb08d334a3de3b083743fb15d8ce7d70226d3dc39ef60b0410ac1b78fe4f4
|