Graham-scan based incremental Delaunay triangulation algorithm with visualization.
Project description
graham-scan-based-incremental-delaunay
A Delaunay triangulation algorithm visualization that incrementally add points during the process and uses Graham Scan to construct the initial triangulation of the iteration.
Documentation
Point.py
Grahamscandelaunay.py
Visual.py
Graham Scan-Based Incremental Delaunay Triangulation Algorithm
Given a list of points:
- Sort the list of points such that:
- the first point is the leftmost, bottommost point, used as the pivot point
- the remaining points are sorted by their slope in ascending order relative to the first point
- Construct the base convex hull using first 3 points (pivot point and two points with the lowest slopes)
- Incrementally add the next sorted point:
- Use Graham Scan to get the convex hull, saving any edges that were made
- Flip the current triangulation to Delaunay
- Repeat until done
Hotkeys
LEFT CLICKwith your mouse create point on where you clicked- Press the
Gkey to generate a random point - Press the
Skey to start the algorithm with your set of points - Press the
SPACEBARto iterate to the next step - Press the
Rkey to reset the algorithm, where you can pressSagain to start with the same set of points - Press the
Ckey to stop the algorithm and clear all the points
Visualization
After starting the algorithm, a triangle will be drawn using three of the points.
- Points
- Black points indicate points that are in the triangulation
- Light Grey points indicate points that have yet to be added to the triangulation
- Red points indicate the most recently added point, and the points that are involved when a circumcircle is displayed
- Dark Red points indicate the point that is on the opposite triangle of a quadrilateral when an edge is being checked if it is Locally Delaunay
- Yellow points indicate the circumcenter of the triangle formed by the Red points
- Edges
- Grey edges indicate the edges in the triangulation
- Green edges indicate the edges that are in the queue to be checked if they are Locally Delaunay
- Blue edges indicate the current edge that is being checked if it is Locally Delaunay A Yellow circle is drawn when the current edge is an inside edge is being checked if it is Locally Delaunay. This is the circumcircle defined by the triangle formed by the Red points, centered on the Yellow circumcenter. If the Dark Red point is within the Yellow circle, then the current edge will be flipped.
When the algorithm is complete, the background will turn green to indicate completion.
Static Walkthrough
Environment and package info
Please make sure you have installed the pyglet and numpy before running the code, Those two package can be installed using pip command
pip install numpy and pip install pyglet
This project has been uploaded to PyPi as a package. You can download the package by the following command:
python3 -m pip install graham-scan-based-incremental-delaunay
After install the package, you can start the project by
python3
and then >>> from grahamscandelaunay import visual
Interesting Examples
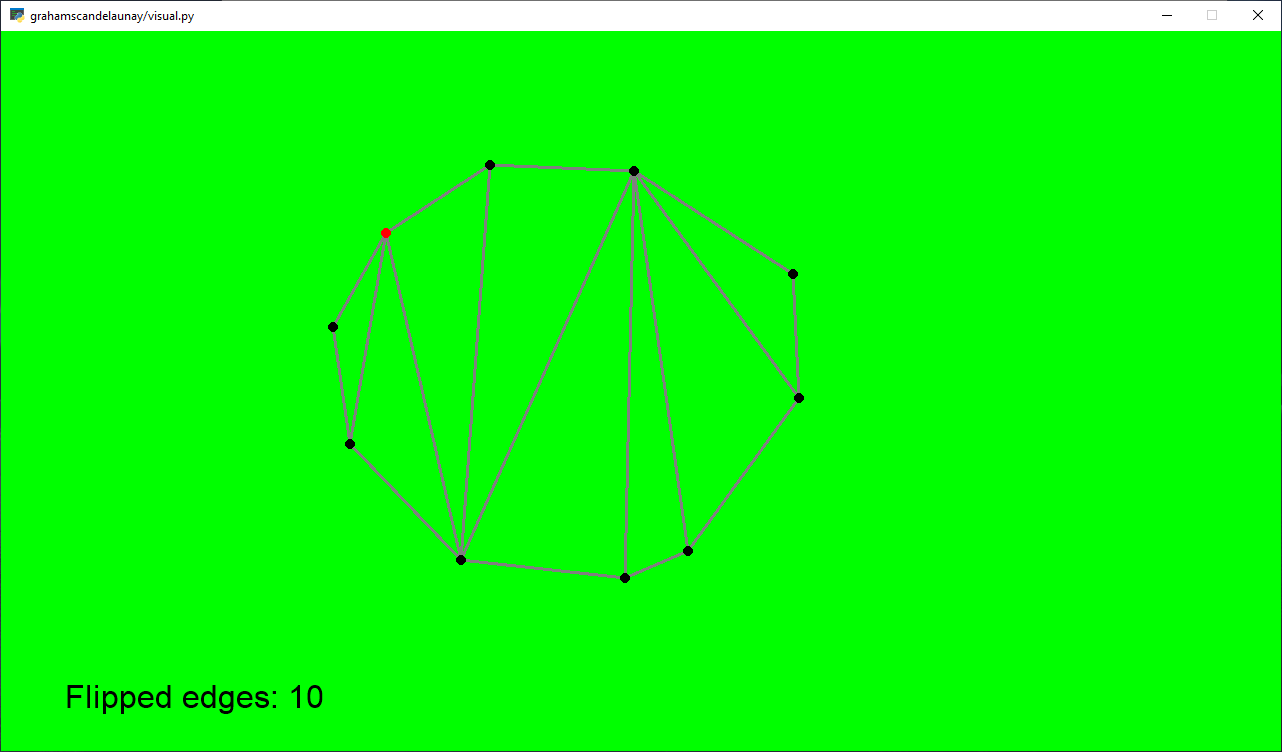
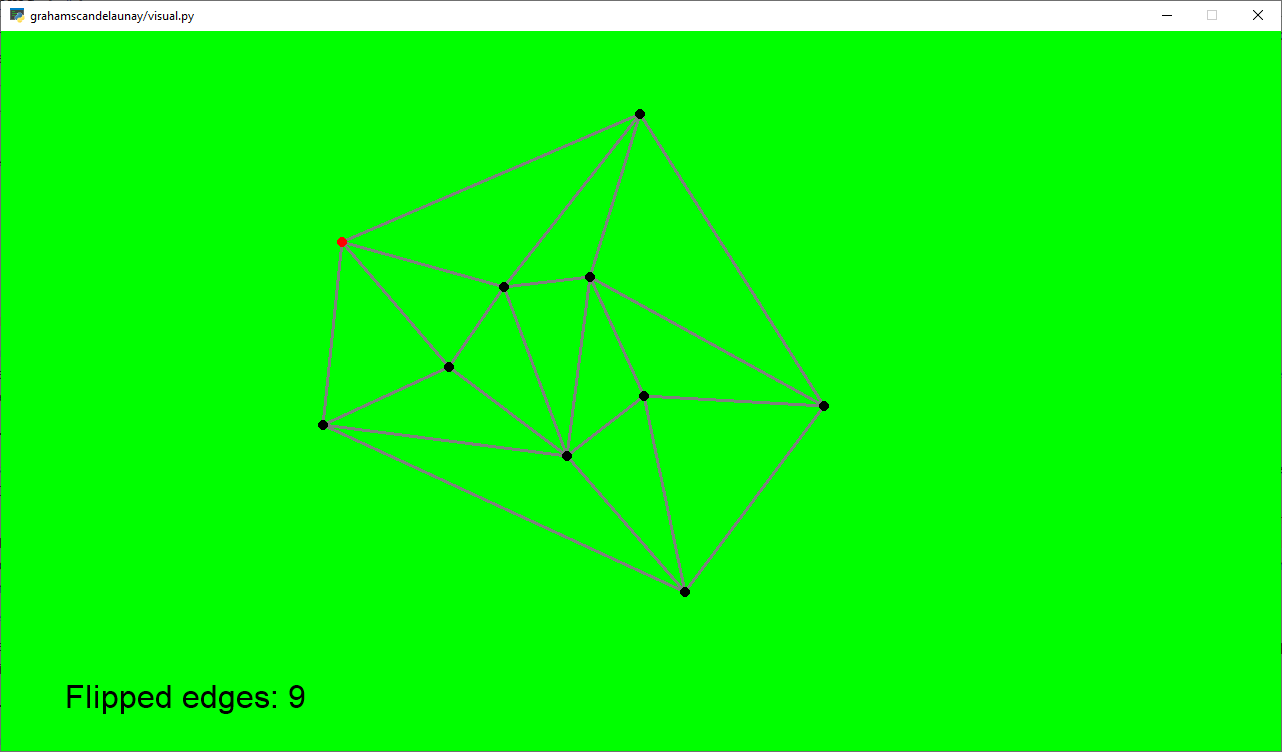
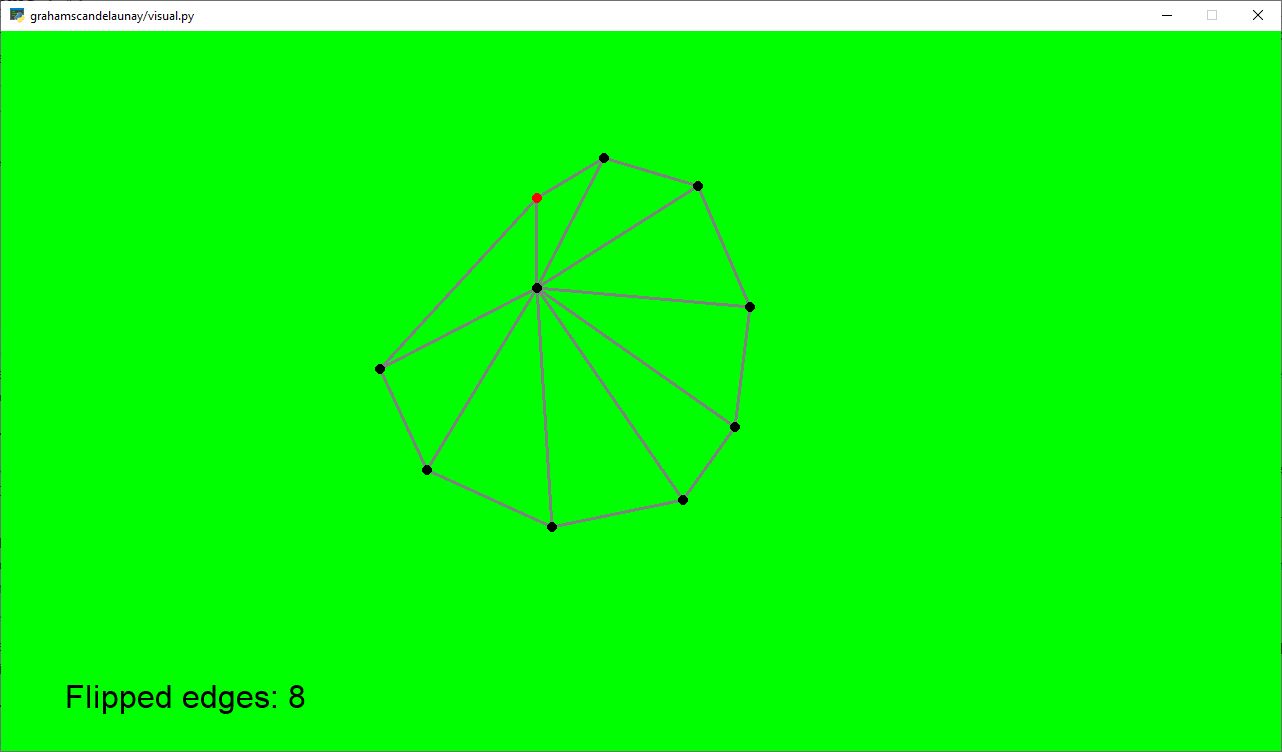
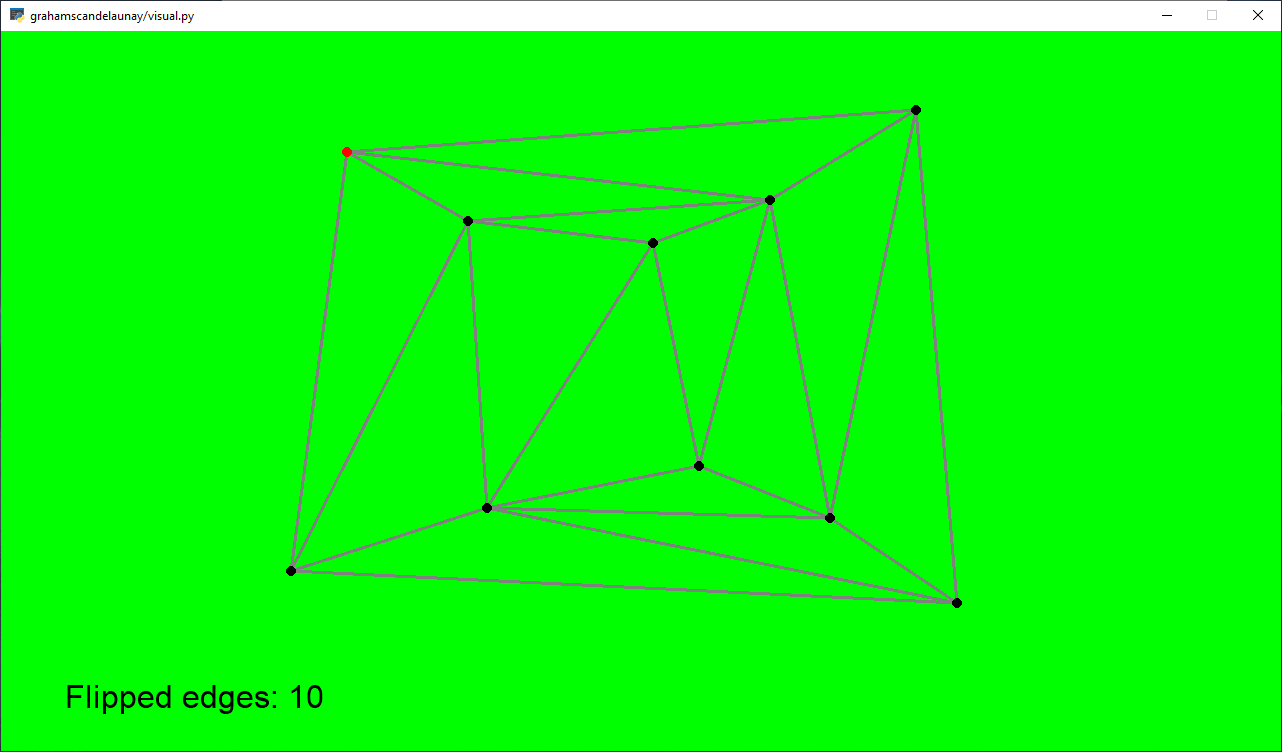
Simple 10-Gon
Pentagon in a Pentagon
Counterclockwise Inward Spiral starting from the left
Hyperbolic Curve (Horizontal Gap) - looks like a suspension bridge
Hyperbolic Curve (Vertical Gap) - looks like an hourglass
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file graham-scan-based-incremental-delaunay-1.0.1.tar.gz.
File metadata
- Download URL: graham-scan-based-incremental-delaunay-1.0.1.tar.gz
- Upload date:
- Size: 9.0 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.4.1 importlib_metadata/4.0.1 pkginfo/1.7.0 requests/2.25.1 requests-toolbelt/0.9.1 tqdm/4.60.0 CPython/3.6.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
15f60b627f3d687f7e4c2dc5825bf960ab53e8bdc4c12e5444de587b79d527f5
|
|
| MD5 |
49f35a92c671d993640a94da034ecfcd
|
|
| BLAKE2b-256 |
269a590e3b2c2b3d46aacb272c66101fc67e3a7837ed82afc4e2358dd2b5c244
|
File details
Details for the file graham_scan_based_incremental_delaunay-1.0.1-py3-none-any.whl.
File metadata
- Download URL: graham_scan_based_incremental_delaunay-1.0.1-py3-none-any.whl
- Upload date:
- Size: 10.2 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.4.1 importlib_metadata/4.0.1 pkginfo/1.7.0 requests/2.25.1 requests-toolbelt/0.9.1 tqdm/4.60.0 CPython/3.6.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
920872f3d3f24296dda333cd8349a3635b513069f78837d2a9e42197fcb19fe6
|
|
| MD5 |
2a6eae63f333d68346871ee5e23f7bdd
|
|
| BLAKE2b-256 |
50361346a9334363ccd6ee975106893ed92e1c944a6e089aa20e62c575f272ff
|