A module to create (almost) hexagonal grids on a sphere
Project description
hexasphere
A module to create (almost) hexagonal grids of variable size on a sphere, fully implemented in python.
description of the grid
base polyhedron
The grid is built by subdividing a base polyhedron into hexagon tiles. The base polyhedron is an icosahedron, which comprises:
- 20 faces (equilateral triangles)
- 12 vertices
- 30 edges
At the vertices of the icosahedron, instead of an hexagon, a pentagon is constructed.
For a given grid resolution n, each edge of the icosahedron goes through exactly n hexagon centers (not counting the polygons found at the ends). The inside of faces is then filled with tile-centers by following a triangular pattern.
This allows to cover the icosahedron. Its surface is then mapped to the sphere using a projection.
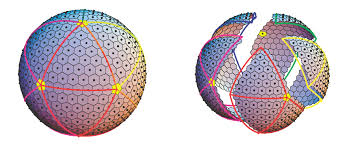
n = 7
projection
There are two available projections in projection module:
-
GnomonicProj: a simple projection, which produces hexagonal tiles about 60% larger (in area) at the corners of a face than at its center. -
SnyderEAProj: a more complex projection, slower to compute (roughly 3x slower than Gnomonic projection), but which preserves areas. The implementation is based on Brenton R S Recht's blog. See there for more details.
hexagon tile identifier
A tile identifier has the following pattern: ?XXXXX-YYYYY-ZZZZZ
?is one of the 20 lettersA ... T, each letter corresponding to one face of the icosahedronXXXXX,YYYYY,ZZZZZare the integer coordinates of the tile in the triangular mesh covering face?. An useful property holds:
XXXXX + YYYYY + ZZZZZ = 2 * (n + 1)
getting started
- Install the package with pip
$ pip install hexasphere
- Import the library in python
from hexasphere import hexgrid, projection
usage
construction of a grid
- Create a
HexGridobject:
my_grid = hexgrid.HexGrid()
- Instantiate a projection system
Projectionassociated with this grid:
my_projection = projection.MyProjection(my_grid)
- Provide the projection system to the grid:
my_grid.projection = my_projection
playing with grid resolutions
- Compute closest grid resolution
nfor any desired hex dimension (in kilometers):
n = my_grid.compute_n_for_radius(0.25)
n = my_grid.compute_n_for_height(0.25)
n = my_grid.compute_n_for_side(0.25)
- Retrieve average hex dimension (in kilometers) for any given resolution
n:
my_grid.compute_radius_for_n(n)
my_grid.compute_height_for_n(n)
my_grid.compute_side_for_n(n)
encoding and decoding
- To find the string identifier of the hexagon to which a geographic point
(lat, lon)belongs, call:
hex_identifier = my_grid.latlon_to_hex(lat, lon, n, out_str=True)[0]
- To find the
(lat, lon)coordinates of the center of an hex, call:
my_grid.hex_to_latlon(hex_identifier, in_str=True)
my_grid.hex_to_latlon(hex_identifier, n, in_str=True) # n is here not required
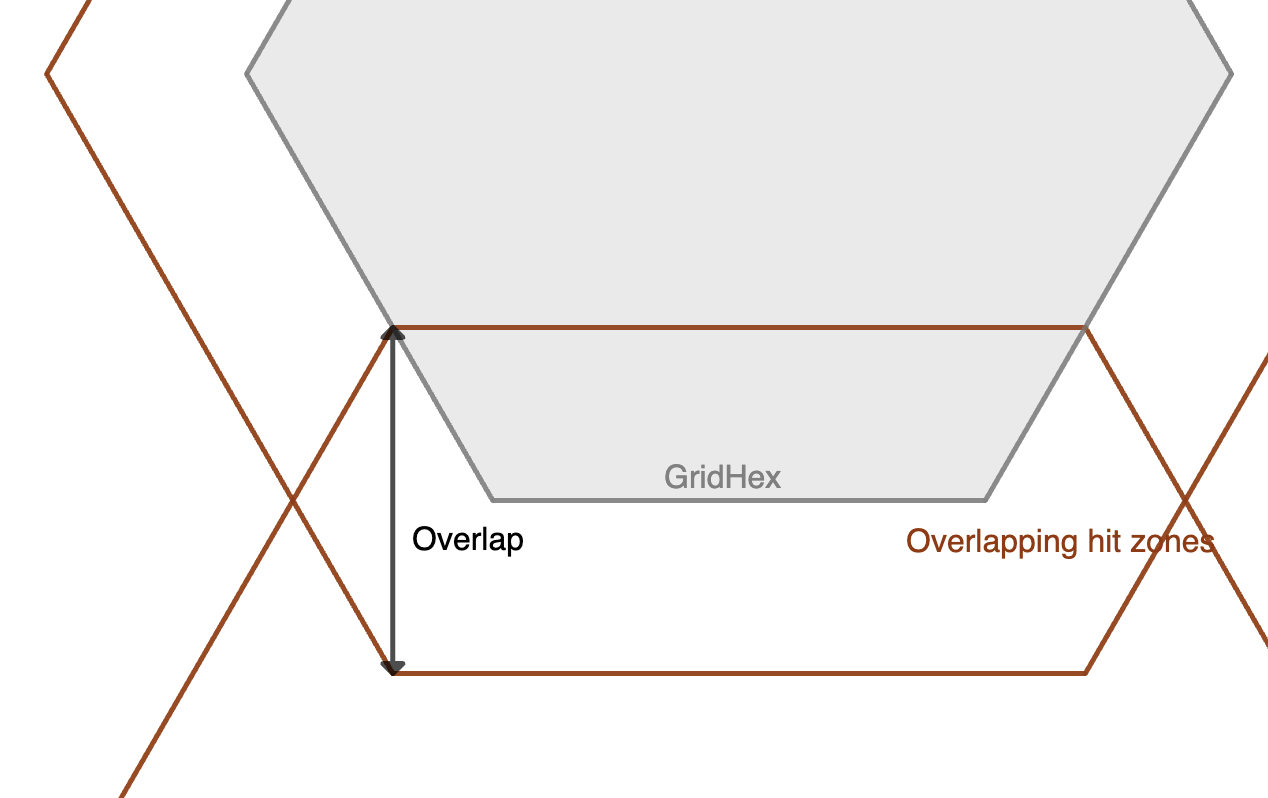
overlapping grids
grid.latlon_to_hex also supports overlapping grids:
value = 12 # Overlap distance (in km)
my_grid.set_overlap(value)
The method grid.latlon_to_hex returns the list of distinct hexes a point of coordinates (lat, lon) belongs to:
hexes_identifier = my_grid.latlon_to_hex(lat, lon, n, out_str=True)
playing with hexagons
retrieving shape data
One can also deal with an Hexagon object instead of an hexagon string identifier:
hex_object = my_grid.latlon_to_hex(lat, lon, n)[0]
hex_object = hexgrid.Hexagon(my_grid, str_id=hexagon_identifier)
The coordinates of the vertices of the corresponding shape can then be retrieved:
shape_coordinates = hex_object.retrieve_polygon(out_latlon=True)
moving on the grid
To retrieve a neighboring hex:
hex_neighbor = hex_object.compute_neighbor(dP=(0, 1, -1))
To retrieve the list of hexes in the k-ring centered on the hex object:
hexes = hex_object.k_ring(k, out_str=True)
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file hexasphere-0.1.0.tar.gz.
File metadata
- Download URL: hexasphere-0.1.0.tar.gz
- Upload date:
- Size: 11.3 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.9.13
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
fcba04c029e37cce4b58fc8cdddb62a94923e64c0a2b57bb775dc826a6956318
|
|
| MD5 |
b219a935888d40590234ae00c7b722e3
|
|
| BLAKE2b-256 |
e0cbc04b64042dbe51f4b35ebc53cfca65be456c74678e1ef027fda664922e25
|
File details
Details for the file hexasphere-0.1.0-py3-none-any.whl.
File metadata
- Download URL: hexasphere-0.1.0-py3-none-any.whl
- Upload date:
- Size: 12.1 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.9.13
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
644137d9c770a9cf2863bc007c1fdf0615ada8e99f32f15d4713d0a2cb10f8a6
|
|
| MD5 |
f87d59bc3c56a9ef1c7eebde902b834d
|
|
| BLAKE2b-256 |
2995a9eac9732b6d15dc985f1e1556c6636c4f2502d209a856b58651f97d90ee
|










