Python 3 implementation of the Hungarian Algorithm for the assignment problem.
Project description
Hungarian Algorithm
A Python 3 graph implementation of the Hungarian Algorithm (a.k.a. the Kuhn-Munkres algorithm), an O(n^3) solution for the assignment problem, or maximum/minimum-weighted bipartite matching problem.
Usage
Install
pip3 install hungarian-algorithm
Import
from hungarian_algorithm import algorithm
Inputs
The function find_matching takes 3 inputs:
algorithm.find_matching(G, matching_type = 'max', return_type = 'list')
G =the bipartite graph (a dictionary of dictionaries*)matching_type = 'max'or'min'(maximum-weighted matching or minimum-weighted matching)return_type = 'list'or'total'(return a list of matched vertices and weights or the total weight*)
*See examples below.
Examples
Example 1 (maximum-weighted matching)
Suppose you're choosing 11 starting positions for a soccer team.
The 11 players submit their top 3 position choices, and it is your job to create the optimal team.
The situation can be modeled with a weighted bipartite graph:
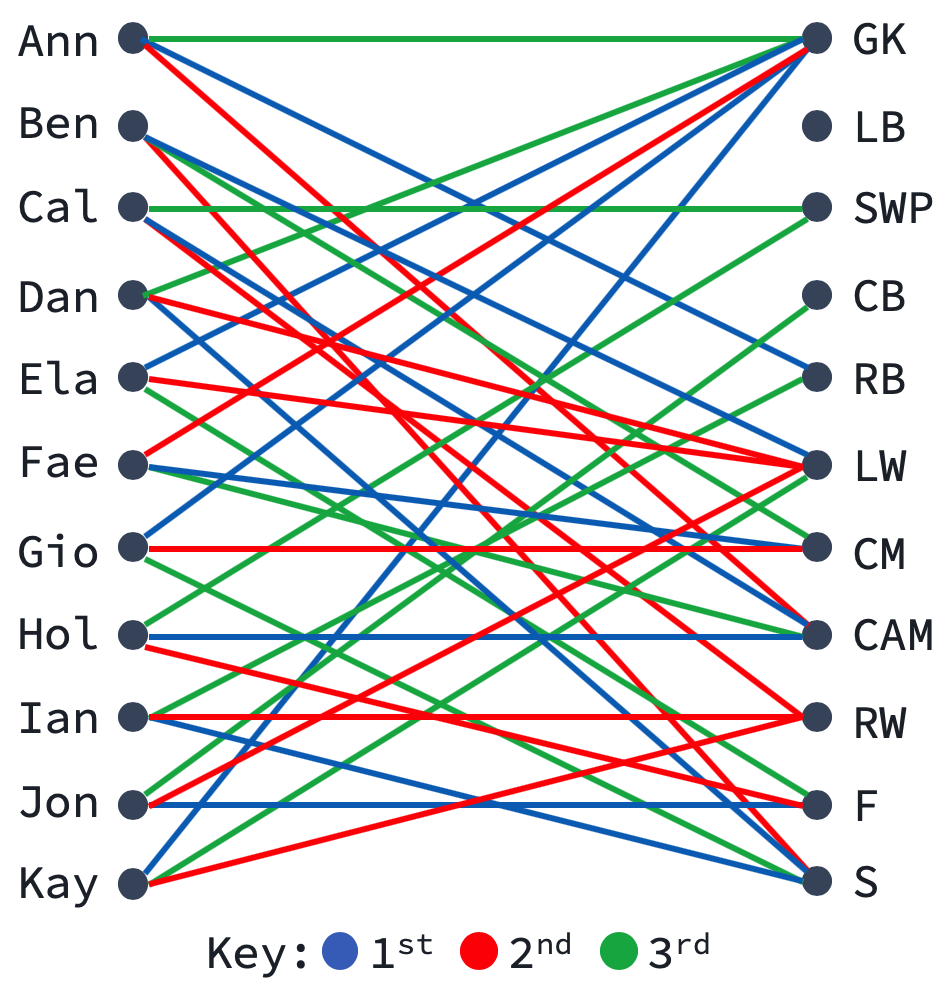
Then, if you assign weight 3 to blue edges, weight 2 to red edges and weight 1 to green edges, your job is simply to find the matching that maximizes total weight. This is the assignment problem, for which the Hungarian Algorithm offers a solution.
Notice: although no one has chosen LB, the algorithm will still assign a player there. In fact, the first step of the algorithm is to create a complete bipartite graph (all possible edges exist), giving new edges weight 0.
Define a weighted bipartite graph in the following manner:
G = {
'Ann': {'RB': 3, 'CAM': 2, 'GK': 1},
'Ben': {'LW': 3, 'S': 2, 'CM': 1},
'Cal': {'CAM': 3, 'RW': 2, 'SWP': 1},
'Dan': {'S': 3, 'LW': 2, 'GK': 1},
'Ela': {'GK': 3, 'LW': 2, 'F': 1},
'Fae': {'CM': 3, 'GK': 2, 'CAM': 1},
'Gio': {'GK': 3, 'CM': 2, 'S': 1},
'Hol': {'CAM': 3, 'F': 2, 'SWP': 1},
'Ian': {'S': 3, 'RW': 2, 'RB': 1},
'Jon': {'F': 3, 'LW': 2, 'CB': 1},
'Kay': {'GK': 3, 'RW': 2, 'LW': 1, 'LB': 0}
}
thus defining a complete bipartite graph G = (L ∪ R, E) with:
- Vertex set L (Players) = {'Ann', 'Ben', 'Cal', 'Dan', 'Ela', 'Fae', 'Gio', 'Hol', 'Ian', 'Jon', 'Kay'}
- Vertex set R (Positions) = {'GK', 'LB', 'SWP', 'CB', 'RB', 'LW', 'CM', 'CAM', 'RW', 'F', 'S'}
- Edge set E = {e = (Player, Position) : for all Players, for all Positions}
- Weight function:
- w(Player, Position) = 3 for a first choice
- w(Player, Position) = 2 for a second choice
- w(Player, Position) = 1 for a third choice
- w(Player, Position) = 0 otherwise
Then pass the graph as an input:
algorithm.find_matching(G, matching_type = 'max', return_type = 'list' )
You will get the output:
[(('Ann', 'RB'), 3), (('Gio', 'CB'), 0), (('Ben', 'LW'), 3), (('Ian', 'RW'), 2), (('Cal', 'CAM'), 3), (('Fae', 'CM'), 3), (('Ela', 'LB'), 0), (('Kay', 'GK'), 3), (('Jon', 'F'), 3), (('Dan', 'S'), 3), (('Hol', 'SWP'), 1)]
If you only need the total weight:
algorithm.find_matching(G, matching_type = 'max', return_type = 'total' )
You will get the output:
24
Example 2 (minimum-weighted matching)
Suppose you manage a group of drivers delivering packages to various locations.
You estimate the time of delivery for each driver to deliver each package, and it is your job to save the most time.
This time, we will model the situation with a matrix:
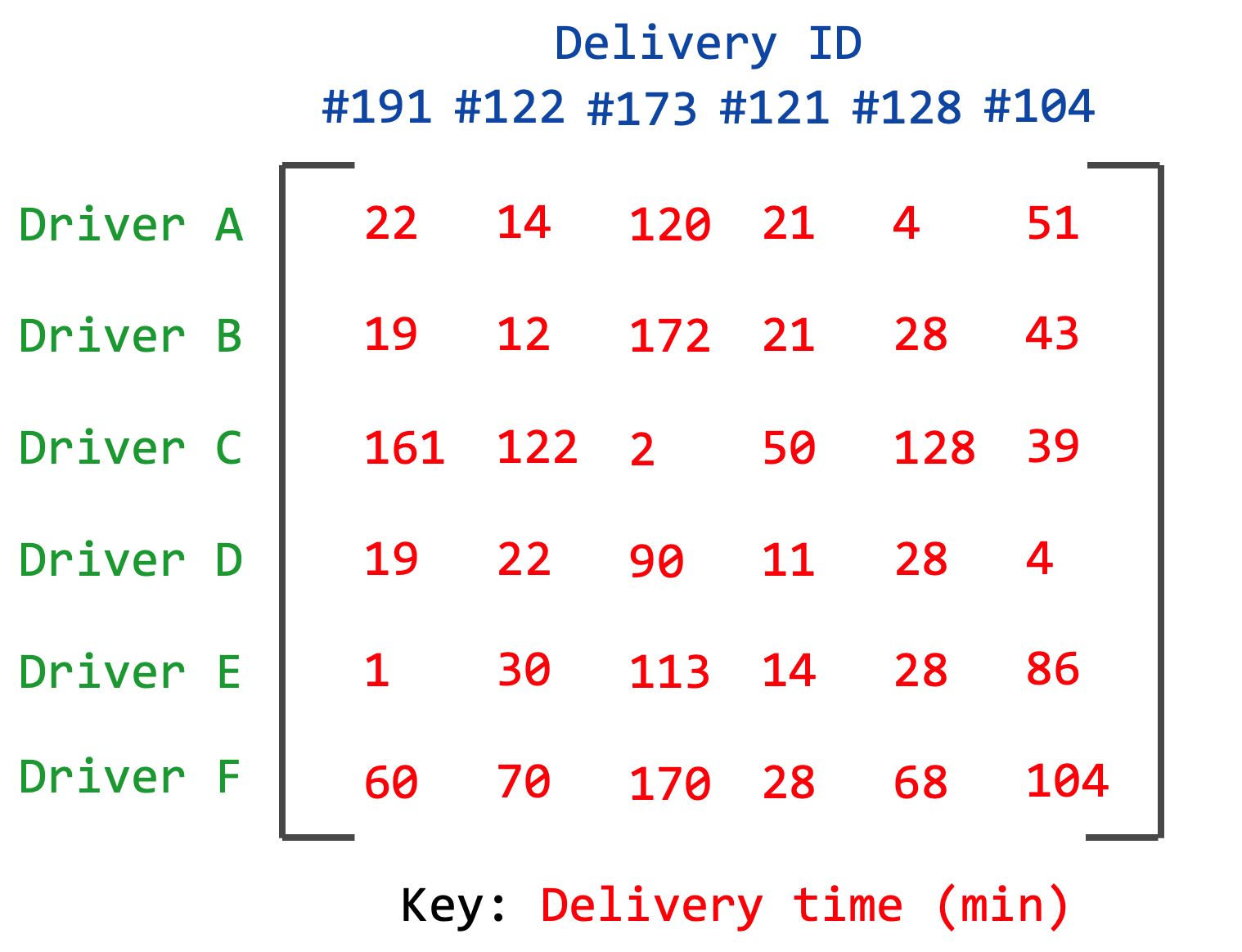
where the values in the matrix give the number of minutes it would take each driver to deliver each package. Again, this is the assignment problem, except this time we seek to find a minimum-weighted matching to minimize the total amount of delivery time.
Define a weighted bipartite graph in the following manner:
H = {
'A': { '#191': 22, '#122': 14, '#173': 120, '#121': 21, '#128': 4, '#104': 51 },
'B': { '#191': 19, '#122': 12, '#173': 172, '#121': 21, '#128': 28, '#104': 43 },
'C': { '#191': 161, '#122': 122, '#173': 2, '#121': 50, '#128': 128, '#104': 39 },
'D': { '#191': 19, '#122': 22, '#173': 90, '#121': 11, '#128': 28, '#104': 4 },
'E': { '#191': 1, '#122': 30, '#173': 113, '#121': 14, '#128': 28, '#104': 86 },
'F': { '#191': 60, '#122': 70, '#173': 170, '#121': 28, '#128': 68, '#104': 104 },
}
Then pass the graph as an input (this time, remember to change matching_type = 'min' to find a minimum-weighted matching):
algorithm.find_matching(H, matching_type = 'min', return_type = 'list' )
You will get the output:
[(('A', '#128'), 4), (('B', '#122'), 12), (('C', '#173'), 2), (('D', '#104'), 4), (('E', '#191'), 1), (('F', '#121'), 28)]
History
The algorithm was published by Harold Kuhn in 1955 paper The Hungarian Method for the Assignment Problem. Kuhn's work relied heavily on that of Hungarian mathematicians Dénes Kőnig and Jenő Egévary.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file hungarian_algorithm-0.1.11.tar.gz.
File metadata
- Download URL: hungarian_algorithm-0.1.11.tar.gz
- Upload date:
- Size: 9.4 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.1.1 pkginfo/1.5.0.1 requests/2.23.0 setuptools/46.1.3 requests-toolbelt/0.9.1 tqdm/4.45.0 CPython/3.7.5
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
fa9d54d976ac3b1b69b4c60353cb47051cafeb45d34a0624dea5907f573d7719
|
|
| MD5 |
446d8926937b3382e1a9867ea344e7c5
|
|
| BLAKE2b-256 |
7e28ac78b5cf5da7788fc839025e360554a8a8c259e5be74c59ca51bf873a3d2
|
File details
Details for the file hungarian_algorithm-0.1.11-py3-none-any.whl.
File metadata
- Download URL: hungarian_algorithm-0.1.11-py3-none-any.whl
- Upload date:
- Size: 10.3 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.1.1 pkginfo/1.5.0.1 requests/2.23.0 setuptools/46.1.3 requests-toolbelt/0.9.1 tqdm/4.45.0 CPython/3.7.5
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a3812cb527329ef09e4ed4c9eba58374677e473a26d637593a9a00d72e49fd49
|
|
| MD5 |
ace09efad3c4936aab24665d8a649e6c
|
|
| BLAKE2b-256 |
08e0117a3f5b9469fa1f74adb7810c465776e2d6145189fbb7bcaa02b5f7c95f
|










