No project description provided
Project description
This library was created for the course IB110 - Introduction to Informatics at MUNI FI.
Below is an overview of how these computational models can be used. Documentation for the functions is located in the files with the implementation.
FINITE AUTOMATA
This library supports deterministic and nondeterministic finite automata. You can find the implementation of these models in the module automaton. Consider class the class located in the base.py as abstract, its only purpose is to avoid duplicities in the implementation of these models.
In order to create an automaton you will need to specify the five-tuple (Q, Σ, δ, q0, F), where:
- The set of states
Qis represented bySet[str] - The set of alphabet symbols
Σis represented bySet[str] - The transition function
δis represented by eitherDFATransitionsorNFATransitions. These types are described below. - The set of final states
Fis represented bySet[str]
There are implemented some helper functions if you need to update the automata automatically. (remove_state(...), add_transition(...), is_valid(), ...)
Deterministic finite automata (DFA)
The implementation for DFA can be found in the file dfa.py with a description of each function.
Example use-case of DFA:
The DFATransitions is an alias to Dict[str, Dict[str, str]]. Keys of this dictionary are symbols where the transition begins. Values are nested dictionaries with alphabet symbols as keys and states where the transition ends as a values.
Example of a transition function
Transition shown above can be implemented like so:
transition_fn: DFATransitions = {
"s1": {
"0": "s2,
"1": "s2,
},
}
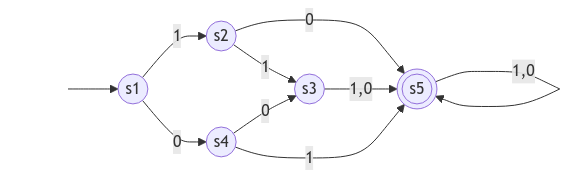
from ib110hw.automaton.dfa import DFA, DFATransitions
dfa_transitions: DFATransitions = {
"s1": {
"1": "s2",
"0": "s4"
},
"s2": {
"1": "s3",
"0": "s5"
},
"s3": {
"1": "s5",
"0": "s5"
},
"s4": {
"1": "s5",
"0": "s3"
},
"s5": {
"1": "s5",
"0": "s5"
},
}
automaton = DFA(
states={"s1", "s2", "s3", "s4", "s5" },
alphabet={"1", "0"},
initial_state="s1",
final_states={"s3"},
transitions=dfa_transitions,
)
automaton.is_accepted("11") # True
automaton.is_accepted("00") # True
automaton.is_accepted("10") # False
Nondeterministic finite automata (NFA)
The implementation for the NFA can be found in the file nfa.py with a description of each function.
Example use-case of NFA:
Transition function of an NFA is described by the NFATransitions. It is an alias to Dict[str, Dict[str, Set[str]]]. It is similar to the DFATransitions but instead of the next-state string, there is a set of next-state strings.
Example of a transition function
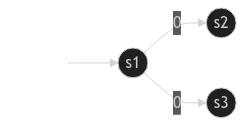
transition_fn: NFATransitions = {
"s1": {
"0": {"s2", "s3"},
"1": set(), # specifying this is unnecessary
},
}
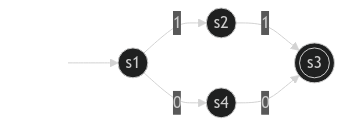
from ib110hw.automaton.nfa import NFA, NFATransitions
nfa_transitions: NFATransitions = {
"s1": {
"1": { "s2" },
"0": { "s4" },
},
"s2": {
"1": { "s3" },
},
"s4": {
"0": { "s3" },
},
}
automaton = NFA(
states={"s1", "s2", "s3", "s4", "s5" },
alphabet={"1", "0"},
initial_state="s1",
final_states={"s3"},
transitions=nfa_transitions,
)
automaton.is_accepted("11") # True
automaton.is_accepted("00") # True
automaton.is_accepted("10") # False
TURING MACHINE
This library supports a deterministic and multi-tape Turing machines. You can find the implementation in the module turing.
Tape
The implementation of the tape for the Turing machine can be found in the file tape.py.
from ib110hw.turing.tape import Tape
tape: Tape = Tape()
tape.write("Hello")
print(tape) # | H | e | l | l | o | |
# ^
tape.move_left()
print(tape) # | | H | e | l | l | o | |
# ^
tape.move_right()
tape.move_right()
print(tape) # | | H | e | l | l | o | |
# ^
tape.write_symbol("a")
print(tape) # | | H | a | l | l | o | |
# ^
tape.clear() # | |
# ^
Deterministic Turing Machine (DTM)
The following DTM checks whether the input string is a palindrome:
from ib110hw.turing.dtm import DTM, DTMTransitions
from ib110hw.turing.tape import Direction
fn: DTMTransitions = {
"init": {
">": ("mark", ">", Direction.RIGHT),
},
"mark": {
"a": ("foundA", "X", Direction.RIGHT),
"b": ("foundB", "X", Direction.RIGHT),
"X": ("accept", "X", Direction.STAY),
"": ("accept", "", Direction.STAY),
},
"foundA": {
"a": ("foundA", "a", Direction.RIGHT),
"b": ("foundA", "b", Direction.RIGHT),
"X": ("checkA", "X", Direction.LEFT),
"": ("checkA", "", Direction.LEFT),
},
"checkA": {
"a": ("back", "X", Direction.LEFT),
"b": ("reject", "b", Direction.STAY),
"X": ("accept", "X", Direction.STAY),
},
"foundB": {
"a": ("foundB", "a", Direction.RIGHT),
"b": ("foundB", "b", Direction.RIGHT),
"X": ("checkB", "X", Direction.LEFT),
"": ("checkB", "", Direction.LEFT),
},
"checkB": {
"a": ("reject", "a", Direction.STAY),
"b": ("back", "X", Direction.LEFT),
"X": ("accept", "X", Direction.STAY),
},
"back": {
"a": ("back", "a", Direction.LEFT),
"b": ("back", "b", Direction.LEFT),
"X": ("mark", "X", Direction.RIGHT)
}
}
machine: DTM = DTM(
states={"init", "mark", "gotoEndA", "checkA", "gotoEndB", "checkB", "accept", "reject"},
input_alphabet={"a", "b"},
acc_states={"accept"},
rej_states={"reject"},
initial_state="init",
transition_function=fn
)
machine.tape.write(">aabbabbaa")
DTM Transition function
A DTM transition function is represented by a nested dictionary defined by the type DTMTransitions.
The keys of this dictionary are states of the turing machine, and values are dictionaries with read symbols as keys and a tuple containing the next state, symbol to be written and the tape head direction as values.
Rule δ(init, >) -> (next, >, 1) can be defined like so:
function: DTMransitions = {
"init": {
">": ("next", ">", Direction.RIGHT)
}
}
Multi-tape Turing Machine (MTM)
The following MTM has the same function as the DTM above:
from ib110hw.turing.mtm import MTM, MTMTransitions
from ib110hw.turing.tape import Direction
function: MTMTransitions = {
"init": {
(">", ""): ("copy", (">", ""), (Direction.RIGHT, Direction.STAY))
},
"copy": {
("a", ""): ("copy", ("a", "a"), (Direction.RIGHT, Direction.RIGHT)),
("b", ""): ("copy", ("b", "b"), (Direction.RIGHT, Direction.RIGHT)),
("", ""): ("goToStart", ("", ""), (Direction.LEFT, Direction.STAY)),
},
"goToStart": {
("a", ""): ("goToStart", ("a", ""), (Direction.LEFT, Direction.STAY)),
("b", ""): ("goToStart", ("b", ""), (Direction.LEFT, Direction.STAY)),
(">", ""): ("check", (">", ""), (Direction.RIGHT, Direction.LEFT))
},
"check": {
("a", "a"): ("check", ("a", "a"), (Direction.RIGHT, Direction.LEFT)),
("b", "b"): ("check", ("b", "b"), (Direction.RIGHT, Direction.LEFT)),
("", ""): ("accept", ("", ""), (Direction.STAY, Direction.STAY)),
("a", "b"): ("reject", ("a", "b"), (Direction.STAY, Direction.STAY)),
("b", "a"): ("reject", ("b", "a"), (Direction.STAY, Direction.STAY)),
}
}
machine: MTM = MTM(
states={"init", "goToEnd", "goToStart", "check", "accept", "reject"},
initial_state="init",
input_alphabet={"a", "b"},
acc_states={"accept"},
rej_states={"reject"},
transition_function=function)
machine.write(">aabbabbaa")
MTM Transition Function
A MTM transition function is represented by a nested dictionary defined by the type MTMTransitions. Compared to DTMTransitions, it takes a tuple of read symbols instead of a singular symbol and a tuple of directions instead of a singular direction. Length of these tuples is the amount of tapes.
Rule δ(init, (>, ␣)) = (next, (>, a), (1, 0)) can be defined like so:
function: MTMransitions = {
"init": {
(">", ""): ("next", (">", "a"), (Direction.RIGHT, Direction.LEFT))
}
}
DTM and MTM Simulation
You can simulate the turing machine using the provided function simulate(...). By default, every step of the Turing machine will be printed to console with 0.5s delay inbetween. This behaviour can be changed by setting the to_console and delay parameters. If the parameter to_console is set to False, the delay will be ignored.
machine.simulate(to_console=True, delay=0.3) # True
If you want to look at the whole history, you can set parameter to_file to True. Every step will be printed to file based on the path provided in the parameter path. Default path is set to ./simulation.txt.
turing.simulate(to_console=False, to_file=True, path="~/my_simulation.txt") # True
The BaseTuringMachine class contains the attribute max_steps to avoid infinite looping. By default, it is set to 100. The computation will stop if the simulation exceeds the value specified by this attribute. This can be an issue on larger inputs, so setting it to a bigger number may be needed.
turing.max_steps = 200
Simulation in Pycharm
For the optimal visualisation of the simulation in PyCharm you need to enable the Terminal emulation.
You can do so by going to Run > Edit configurations ... and then checking the Emulate terminal in output console box.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.