An all-purpose pythonic genetic algorithm
Project description
NaturalSelection 
An all-purpose pythonic genetic algorithm, which also has built-in hyperparameter tuning support for neural networks.
Installation
$ pip install naturalselection
Usage
Here is a toy example optimising a pair of numbers with respect to division.
>>> import naturalselection as ns
>>>
>>> Pair = ns.Genus(x = range(1, 10000), y = range(1, 10000))
>>> def division(number):
... return number.x / number.y
...
>>> pairs = ns.Population(genus = Pair, size = 100, fitness_fn = division)
>>> history = pairs.evolve(generations = 50, progress_bars = 1)
Evolving population: 100%|█████████████████████| 50/50 [00:09<00:00, 5.28it/s]
>>>
>>> history.fittest
{'genome': {'x': 9974, 'y': 4}, 'fitness': 2493.5}
>>>
>>> history.plot()
We can also easily solve the classical OneMax problem, which is about finding the bit-string of a given length with all 1's. Here we set goal=100 in the evolve function to allow for early stopping if we reach our goal before the maximum number of generations, which we here set to 1000.
>>> import naturalselection as ns
>>>
>>> # Length of the bit strings
>>> N = 100
>>> BitString = ns.Genus(**{f'x{n}' : (0,1) for n in range(N)})
>>>
>>> def sum_bits(bitstring):
... return sum(bitstring.get_genome().values())
>>>
>>> bitstrings = ns.Population(
... genus = BitString,
... size = 2,
... fitness_fn = sum_bits
... )
>>>
>>> history = bitstrings.evolve(
... generations = 10000,
... goal = 100,
... progress_bars = 1
... )
Evolving population: 45%|████████ | 4480/10000 [01:00<01:58, 46.43it/s]
>>>
>>> history.plot()
Lastly, here is an example of finding a vanilla feedforward neural network to model MNIST.
>>> import naturalselection as ns
>>> from tensorflow.keras.utils import to_categorical
>>> import mnist
>>>
>>> # Standard train and test sets for MNIST
>>> X_train = ((mnist.train_images() / 255) - 0.5).reshape((-1, 784))
>>> Y_train = to_categorical(mnist.train_labels())
>>> X_val = ((mnist.test_images() / 255) - 0.5).reshape((-1, 784))
>>> Y_val = to_categorical(mnist.test_labels())
>>>
>>> fitness_fn = ns.get_nn_fitness_fn(
... train_val_sets = (X_train, Y_train, X_val, Y_val),
... loss_fn = 'binary_crossentropy',
... score = 'accuracy',
... output_activation = 'softmax',
... max_training_time = 60
... )
>>>
>>> # The above fitness function will actually output 1 / (1 - accuracy) to
>>> # enable an unbounded range for which the algorithm performs better, so
>>> # below we set `post_fn` to be the inverse of this, to get the accuracy
>>> fnns = ns.Population(
... genus = ns.FNN(),
... size = 50,
... fitness_fn = fitness_fn,
... post_fn = lambda x: 1 - (1 / x)
... )
>>> history = fnns.evolve(generations = 20)
Evolving population: 100%|██████████████████| 20/20 [3:05:08<00:00, 403.65s/it]
Computing fitness for gen 20: 100%|█████████████| 24/24 [6:01<00:00, 15.06s/it]
>>>
>>> history.fittest
{'genome': {'optimizer': 'adam', 'hidden_activation': 'relu',
'batch_size': 1024, 'initializer': 'lecun_normal', 'input_dropout': 0.0,
'layer0': 0, 'dropout0': 0.1, 'layer1': 512, 'dropout1': 0.0, 'layer2': 128,
'dropout2': 0.0, 'layer3': 256, 'dropout3': 0.3, 'layer4': 128,
'dropout4': 0.0}, 'fitness': 0.9808}
>>>
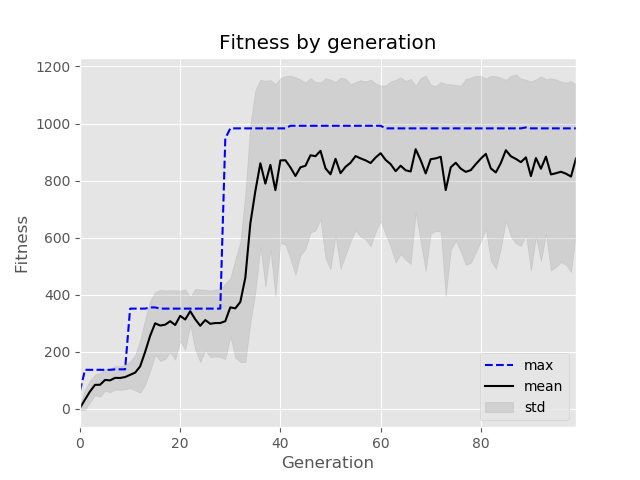
>>> history.plot(title = "Average validation accuracy by generation")
As layer0 = 0 this of course means that the architecture here is [512, 128, 256, 128] with 10% input dropout and 30% dropout after the layer with 256 neurons, along with the adam optimiser, lecun_normal initialiser, relu activation for the hidden layers and a batch size of 1024. Note that this large batch size is encouraged by the fact that we set max_training_time = 60 as larger batch sizes tend to perform better on the short term.
Algorithmic details
The algorithm follows the standard blueprint for a genetic algorithm as e.g. described on this Wikipedia page, which roughly goes like this:
- An initial population is constructed
- Fitness values for all organisms in the population are computed
- A subset of the population (the elite pool) is selected
- A subset of the population (the breeding pool) is selected
- Pairs from the breeding pool are chosen, who will breed to create a new "child" organism with genome a combination of the "parent" organisms. Continue breeding until the the children and the elites constitute a population of the same size as the original
- A subset of the children (the mutation pool) is selected
- Every child in the mutation pool is mutated, meaning that they will have their genome altered in some way
- Go back to step 2
We now describe the individual steps in this particular implementation in more detail. Note that step 3 is sometimes left out completely, but since that just corresponds to an empty elite pool I decided to keep it in, for generality.
Step 1: Constructing the initial population
The population is a uniformly random sample of the possible genome values as dictated by the genus, which is run when a new Population object is created. Alternatively, you may set the initial_genome to a whatever genome you would like, which will make a completely homogenous population consisting only of organisms of this genome (mutations will create some diversity in each generation).
>>> pairs = ns.Population(
... genus = Pair,
... size = 100,
... fitness_fn = division,
... initial_genome = {'x' : 9750, 'y' : 15}
... )
Evolving population: 100%|███████████████████| 100/100 [00:09<00:00, 5.28it/s]
>>>
>>> self.fittest
{'genome' : {'x' : 9846, 'y' : 1}, 'fitness' : 9846.0}
Step 2: Compute fitness values
This happens in the get_fitness function which is called by the evolve function. These computations will by default be computed in parallel for each CPU core, so in the MNIST example above this will require 4-5gb RAM. Alternatively, the number of parallel computations can be explicitly set by setting workers to a small value, or disable the parallel computations completely by setting multiprocessing = False.
Steps 3 & 4: Selecting elite pool and breeding pool
These two pools are selected in exactly the same way, only differing in the amount of organisms in each pool, where the default elitism_rate is 5% and breeding_rate is 80%. In the pool selection it chooses the population based on the distribution with density function the fitness value divided by the sum of all fitness values of the population. This means that the higher fitness score an organism has, the more likely it is for it to be chosen to be a part of the pool. The precise implementation of this follows the algorithm specified on this Wikipedia page.
Step 5: Breeding
In this implementation the parent organisms are chosen uniformly at random, and when determining the value of the child's genome, every gene is a uniformly random choice between its parents' values for that particular gene.
Step 6: Selection of mutation pool
The mutation pool is chosen uniformly at random in contrast with the other two pools, as otherwise we would suddenly be more likely to "mutate away" many of the good genes of our fittest organisms. The default mutation_rate is 20%.
Step 7: Mutation
This implementation is roughly the bit string mutation, where every gene of the organism has a 1/n chance of being uniformly randomly replaced by another gene, with n being the number of genes in the organism's genome. This means that, on average, mutation causes one gene to be altered.
Possible future extensions
These are the ideas that I have thought of implementing in the future. Check the ongoing process on the dev branch.
- Enable support for CNNs
- Enable support for RNNs and LSTMs
- Include an option to have dependency relations between genes. In a neural network setting this could include the topology as a gene on which all the layer-specific genes depend upon, which would be similar to the approach taken in this paper.
License
This project is licensed under the MIT License.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file naturalselection-0.3.4.tar.gz.
File metadata
- Download URL: naturalselection-0.3.4.tar.gz
- Upload date:
- Size: 16.6 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.13.0 pkginfo/1.5.0.1 requests/2.18.4 setuptools/41.0.1 requests-toolbelt/0.8.0 tqdm/4.19.5 CPython/3.6.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 2d675ed503b505d5f00be206cc823c83c7ebca9aa91d883f8aebf7aa78833d34 |
|
| MD5 | d58795e483d4f368c6bc82c4d114edef |
|
| BLAKE2b-256 | d27d0f5726f2062086540a581177521bfc41b84ed02ba684a3bbe4af0a56560b |
File details
Details for the file naturalselection-0.3.4-py3-none-any.whl.
File metadata
- Download URL: naturalselection-0.3.4-py3-none-any.whl
- Upload date:
- Size: 14.6 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.13.0 pkginfo/1.5.0.1 requests/2.18.4 setuptools/41.0.1 requests-toolbelt/0.8.0 tqdm/4.19.5 CPython/3.6.8
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | e70518ae0fa5113f280d0ff1622f8fcdbda5203537e5c6609911f3aa1f1dc2ba |
|
| MD5 | 74452cb0a2a80ab918a3553bd697f732 |
|
| BLAKE2b-256 | 8f26ba05912e180eef9e9b5ef6172c281daeef90432eb833e0de15395a1f634a |