Python library for primes algorithms
Project description
Installation
To install the package use pip:
pip install nprime
Introduction
Some algorithm on prime numbers. You can find all the functions in the file nprime/pryprime.py
Algorithm developed :
Eratosthenes sieve based
Fermat’s test (based on Fermat’s theorem)
Prime generating functions
Miller Rabin predictive algorithm
Specifications
Language: Python 3.5.2
Package:
Basic python packages were preferred
Matplotlib v2.1 - graph and math
Integration and pipeline
Code quality is monitored through codacity. For the tests coverage, there’s codecov which is run during the Travis CI pipeline.
Math
Here are a bit of information to help understand some of the algorithms
Congruence
“≡” means congruent, a ≡ b (mod m) implies that m / (a-b), ∃ k ∈ Z that verifies a = kn + b
which implies:
a ≡ 0 (mod n) <-> a = kn <-> "a" is divisible by "n"
Strong Pseudoprime
A strong pseudoprime to a base a is an odd composite number n with n-1 = d·2^s (for d odd) for which either a^d = 1(mod n) or a^(d·2^r) = -1(mod n) for some r = 0, 1, ..., s-1
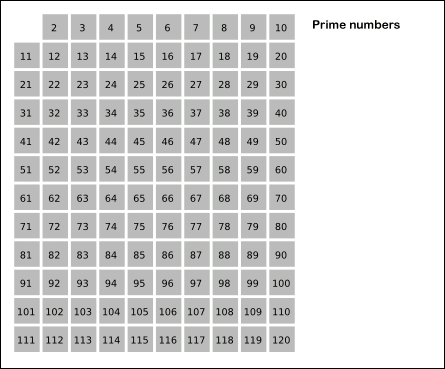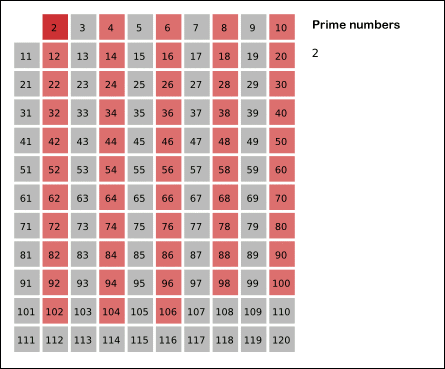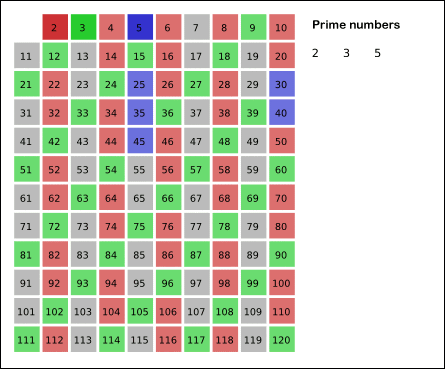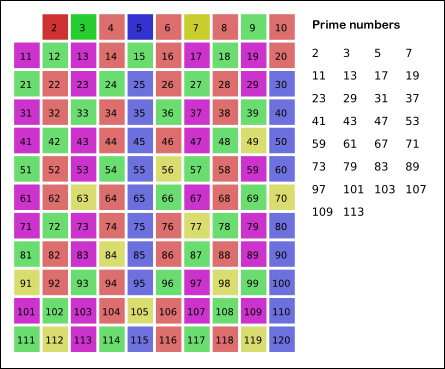
Erathostene’s Sieve
How to use
Implementation of the sieve of erathostenes that discover the primes and their composite up to a limit. It returns a dictionary: - the key are the primes up to n - the value is the list of composites of these primes up to n
from nprime import sieve_eratosthenes
# With as a parameter the upper limit
sieve_eratosthenes(10)
>> {2: [4, 6, 8, 10], 3: [9], 5: [], 7: []}The previous behaviour can be called using the trial_division which uses the Trial Division algorithm
Theory
This sieve mark as composite the multiple of each primes. It is an efficient way to find primes. For n ∈ N with n > 2 and for ∀ a ∈[2, ..., √n] then n/a ∉ N is true.
Fermat’s Theorem
How to use
A Probabilistic algorithm taking t randoms numbers a and testing the Fermat’s theorem on number n > 1 Prime probability is right is 1 - 1/(2^t) Returns a boolean: True if n passes the tests.
from nprime import fermat
# With n the number you want to test
fermat(n)Theory
If n is prime then ∀ a ∈[1, ..., n-1]
a^(n-1) ≡ 1 (mod n) ⇔ a^(n-1) = kn + 1
Miller rabin
How to use
A probabilistic algorithm which determines whether a given number (n > 1) is prime or not. The miller_rabin tests is repeated t times to get more accurate results. Returns a boolean: True if n passes the tests.
from nprime import miller_rabin
# With n the number you want to test
miller_rabin(n)Theory
For n ∈ N and n > 2, Take a random a ∈ {1,...,n−1} Find d and s such as with n - 1 = 2^s * d (with d odd) if (a^d)^2^r ≡ 1 mod n for all r in 0 to s-1 Then n is prime.
The test output is false of 1/4 of the “a values” possible in n, so the test is repeated t times.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file nprime-1.2.1.tar.gz.
File metadata
- Download URL: nprime-1.2.1.tar.gz
- Upload date:
- Size: 29.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/1.15.0 pkginfo/1.5.0.1 requests/2.24.0 setuptools/50.3.0 requests-toolbelt/0.9.1 tqdm/4.50.0 CPython/3.5.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
5f6189cd3652e2e756f731c8358fc9a3989a27fcde6075afe86ae3428036c693
|
|
| MD5 |
70ce9c6c103ecbce9f4c6a50972e7827
|
|
| BLAKE2b-256 |
1059dab82ecee88c48418e9cc5997d9d43d5bc6247e9fa74c1af05b95e83cc05
|