Optimal Transport Tools (OTT)
See the full documentation.
What is OTT-JAX?
A JAX powered library to solve a wide variety of problems leveraging optimal transport theory, at scale and on accelerators.
In particular, OTT-JAX implements various discrete solvers to match two point clouds, notably the Sinkhorn algorithm implemented to work on various geometric domains and sped up using various tweaks (scheduling, momentum, acceleration, initializations) and extensions (low-rank).
These algorithms power the resolution of more advanced problems (Gromov-Wasserstein, Wasserstein barycenter) to compare point clouds in versatile settings.
On top of these discrete solvers, we also propose implementations of neural network approaches. Given an source/target pair of measure, they output a neural net network that seeks to approximation their optimal transport map.
OTT-JAX is led by a team of researchers at Apple, with past contributions from Google and Meta researchers, as well as academic partners, including TU München, Oxford, ENSAE/IP Paris, ENS Paris and the Hebrew University.
Installation
Install OTT-JAX from PyPI as:
pip install ott-jax
or with conda via conda-forge as:
conda install -c conda-forge ott-jax
What is optimal transport?
Optimal transport can be loosely described as the branch of mathematics and optimization that studies matching problems: given two families of points, and a cost function on pairs of points, find a "good" (low cost) way to associate bijectively to every point in the first family another in the second.
Such problems appear in all areas of science, are easy to describe, yet hard to solve. Indeed, while matching optimally two sets of $n$ points using a pairwise cost can be solved with the Hungarian algorithm, solving it costs an order of $O(n^3)$ operations, and lacks flexibility, since one may want to couple families of different sizes.
Optimal transport extends all of this, through faster algorithms (in $n^2$ or even linear in $n$) along with numerous generalizations that can help it handle weighted sets of different size, partial matchings, and even more evolved so-called quadratic matching problems.
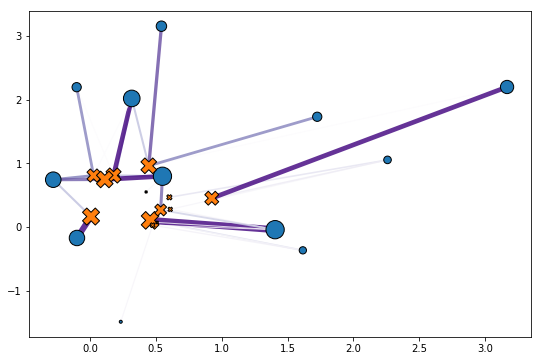
In the simple toy example below, we compute the optimal coupling matrix between two point clouds sampled randomly (2D vectors, compared with the squared Euclidean distance):
Example
import jax
import jax.numpy as jnp
from ott.geometry import pointcloud
from ott.problems.linear import linear_problem
from ott.solvers import linear
from ott.tools import plot
# sample two point clouds and their weights.
rngs = jax.random.split(jax.random.key(42), 4)
n, m, d = 6, 11, 2
x = jax.random.uniform(rngs[0], (n,d))
y = jax.random.uniform(rngs[1], (m,d))
a = jax.random.uniform(rngs[2], (n,)) +.2
b = jax.random.uniform(rngs[3], (m,)) +.2
a, b = a / jnp.sum(a), b / jnp.sum(b)
# instantiate geometry object to compare point clouds.
geom = pointcloud.PointCloud(x, y)
# compute coupling using the Sinkhorn algorithm.
out = jax.jit(linear.solve)(geom,a,b)
# plot
plot.Plot()(out)
The call to solve(prob) above works out the optimal transport solution. The out object contains a transport matrix
(here of size $12\times 14$) that quantifies the association strength between each point of the first point cloud, to one or
more points from the second, as illustrated in the plot below. We provide more flexibility to define custom cost
functions, objectives, and solvers, as detailed in the full documentation. The last command displays the transport matrix by using a Plot object.
Citation
If you have found this work useful, please consider citing this reference:
@article{cuturi2022optimal,
title={Optimal Transport Tools (OTT): A JAX Toolbox for all things Wasserstein},
author={Cuturi, Marco and Meng-Papaxanthos, Laetitia and Tian, Yingtao and Bunne, Charlotte and
Davis, Geoff and Teboul, Olivier},
journal={arXiv preprint arXiv:2201.12324},
year={2022}
}
See also
The moscot package for OT analysis of multi-omics data uses OTT as a backbone.
1 maintainer
Release files for ott-jax 0.6.0
For a detailed explanation of source distributions (sdists) and built distributions (wheels), please see the package formats documentation.
Source distribution (sdist)
| File | Size | Uploaded | |
|---|---|---|---|
| ott_jax-0.6.0.tar.gz | 233.9 kB | Details |
Built distribution (wheel)
| File | Interpreter | ABI | Platform | Reset |
|---|---|---|---|---|
| ott_jax-0.6.0-py3-none-any.whl | Python 3 | none | any | Details |
Total release size: 543.5 kB
Release files / ott_jax-0.6.0.tar.gz
| Download URL | ott_jax-0.6.0.tar.gz |
|---|---|
| Size | 233.9 kB |
| Tags | Source |
|
SHA-256 checksum How to use checksums |
86fda8aea68a6c29c989b1be2fc8bc7e5344e6353d3e486a3edbc36364b07483
|
|
BLAKE2b-256 checksum How to use checksums |
8a46a45f351fcfaa456a42bc318d7ee8641ff4cef758aace295ae4a27459ac3a
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
Yes |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Provenance
Provenance describes where a file came from. On PyPI, provenance is shared via attestations, which provide a verifiable record of the build or publishing details. View details, limitations and caveats.
PyPI Publish Attestation
PyPI verified that this artifact, at this checksum, originated from the publisher listed below.
Signed by GitHub Actions, verified by PyPI on Nov 4, 2025.
Transparency logRelease files / ott_jax-0.6.0-py3-none-any.whl
| Download URL | ott_jax-0.6.0-py3-none-any.whl |
|---|---|
| Size | 309.7 kB |
| Tags | Python 3 |
|
SHA-256 checksum How to use checksums |
89d7ee73ae105a56385b66a43e9acd5ae070e66d991efc56047ab47cc756f3e6
|
|
BLAKE2b-256 checksum How to use checksums |
46780f66915250058498915b3944ac7eccb0da5ce1f5984664fbb6a448cf73db
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
Yes |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Provenance
Provenance describes where a file came from. On PyPI, provenance is shared via attestations, which provide a verifiable record of the build or publishing details. View details, limitations and caveats.
PyPI Publish Attestation
PyPI verified that this artifact, at this checksum, originated from the publisher listed below.
Signed by GitHub Actions, verified by PyPI on Nov 4, 2025.
Transparency log
