Package for creating penalty models.
Project description





penaltymodel
One approach to solve a constraint satisfaction problem (CSP) using an Ising model or a QUBO, is to map each individual constraint in the CSP to a ‘small’ Ising model or QUBO. This mapping is called a penalty model.
Imagine that we want to map an AND clause to a QUBO. In other words, we want the solutions to the QUBO (the solutions that minimize the energy) to be exactly the valid configurations of an AND gate. Let z = AND(x_1, x_2).
Before anything else, let’s import that package we will need.
import penaltymodel as pm
import dimod
import networkx as nxNext, we need to determine the feasible configurations that we wish to target (by making the energy of these configuration in the binary quadratic low). Below is the truth table representing an AND clause.
x_1 |
x_2 |
z |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
The rows of the truth table are exactly the feasible configurations.
feasible_configurations = [{'x1': 0, 'x2': 0, 'z': 0},
{'x1': 1, 'x2': 0, 'z': 0},
{'x1': 0, 'x2': 1, 'z': 0},
{'x1': 1, 'x2': 1, 'z': 1}]At this point, we can get a penalty model
bqm, gap = pm.get_penalty_model(feasible_configurations)However, if we know the QUBO, we can build the penalty model ourselves. We observe that for the equation:
E(x_1, x_2, z) = x_1 x_2 - 2(x_1 + x_2) z + 3 z + 0We get the following energies for each row in our truth table.
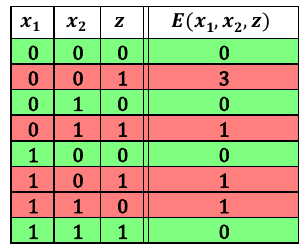
We can see that the energy is minimized on exactly the desired feasible configurations. So we encode this energy function as a QUBO. We make the offset 0.0 because there is no constant energy offset.
qubo = dimod.BinaryQuadraticModel({'x1': 0., 'x2': 0., 'z': 3.},
{('x1', 'x2'): 1., ('x1', 'z'): 2., ('x2', 'z'): 2.},
0.0,
dimod.BINARY)We know from the table that our ground energy is 0, but we can calculate it using the qubo to check that this is true for the feasible configuration (0, 1, 0).
ground_energy = qubo.energy({'x1': 0, 'x2': 1, 'z': 0})The last value that we need is the classical gap. This is the difference in energy between the lowest infeasible state and the ground state.
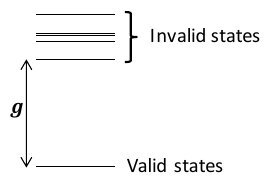
With all of the pieces, we can now build the penalty model.
classical_gap = 1
p_model = pm.PenaltyModel.from_specification(spec, qubo, classical_gap, ground_energy)Installation
To install the core package:
pip install penaltymodelLicense
Released under the Apache License 2.0
Contributing
Ocean’s contributing guide has guidelines for contributing to Ocean packages.
Release Notes
penaltymodel makes use of reno to manage its release notes.
When making a contribution to penaltymodel that will affect users, create a new release note file by running
reno new your-short-descriptor-hereYou can then edit the file created under releasenotes/notes/. Remove any sections not relevant to your changes. Commit the file along with your changes.
See reno’s user guide for details.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file penaltymodel-1.2.0.tar.gz.
File metadata
- Download URL: penaltymodel-1.2.0.tar.gz
- Upload date:
- Size: 33.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.1.1 CPython/3.9.20
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
ea60299743df2cc26c80eda47388a7c1de502a29213241027e0a9c10fced9b69
|
|
| MD5 |
7ed63a3e14e3d72149a7902ffc278507
|
|
| BLAKE2b-256 |
31ffeae8f67046e6123f33e2bb7cb80be13f74476f426895578ed055812fe2e4
|
File details
Details for the file penaltymodel-1.2.0-py3-none-any.whl.
File metadata
- Download URL: penaltymodel-1.2.0-py3-none-any.whl
- Upload date:
- Size: 36.9 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/5.1.1 CPython/3.9.20
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
7496f3d7617d3fce1c863e06419601e9040428f08aa91d878e5e52895d93d8b6
|
|
| MD5 |
e5d9aaaf1001dd7a0fd389503be5273b
|
|
| BLAKE2b-256 |
d96efbde4d088eda36e9e1664d5c9196d29b43d3e76792fb579aaab0089955bd
|











