Welcome to pentapy
Purpose
pentapy is a toolbox to deal with pentadiagonal matrices in Python.
Pentadiagonal linear equation systems arise in many areas of science and engineering: e.g. when solving differential equations, in interpolation problems, or in numerical schemes like finite difference.
Installation
The package can be installed via pip. On Windows you can install WinPython to get Python and pip running.
pip install pentapy
There are pre-built wheels for Linux, MacOS and Windows for most Python versions.
To get the scipy solvers running, you have to install scipy or you can use the following extra argument:
pip install pentapy[all]
Instead of "all" you can also typ "scipy" or "umfpack" to get one of these specific packages.
Citation
If you use pentapy in your publication, please cite it:
Müller, (2019). pentapy: A Python toolbox for pentadiagonal linear systems. Journal of Open Source Software, 4(42), 1759, https://doi.org/10.21105/joss.01759
To cite a certain release, have a look at the Zenodo site: https://doi.org/10.5281/zenodo.2587158
References
The solver is based on the algorithms PTRANS-I and PTRANS-II presented by Askar et al. 2015.
Documentation and Examples
You can find the documentation under https://pentapy.readthedocs.org.
Solving a pentadiagonal linear equation system
This is an example of how to solve a LES with a pentadiagonal matrix.
import numpy as np
import pentapy as pp
size = 1000
# create a flattened pentadiagonal matrix
M_flat = (np.random.random((5, size)) - 0.5) * 1e-5
V = np.random.random(size) * 1e5
# solve the LES with M_flat as row-wise flattened matrix
X = pp.solve(M_flat, V, is_flat=True)
# create the corresponding matrix for checking
M = pp.create_full(M_flat, col_wise=False)
# calculate the error
print(np.max(np.abs(np.dot(M, X) - V)))
This should give something like:
4.257890395820141e-08
Performance
In the following a couple of solvers for pentadiagonal systems are compared:
- Solver 1: Standard linear algebra solver of Numpy
np.linalg.solve - Solver 2:
scipy.sparse.linalg.spsolve - Solver 3: Scipy banded solver
scipy.linalg.solve_banded - Solver 4: pentapy.solve with
solver=1 - Solver 5: pentapy.solve with
solver=2
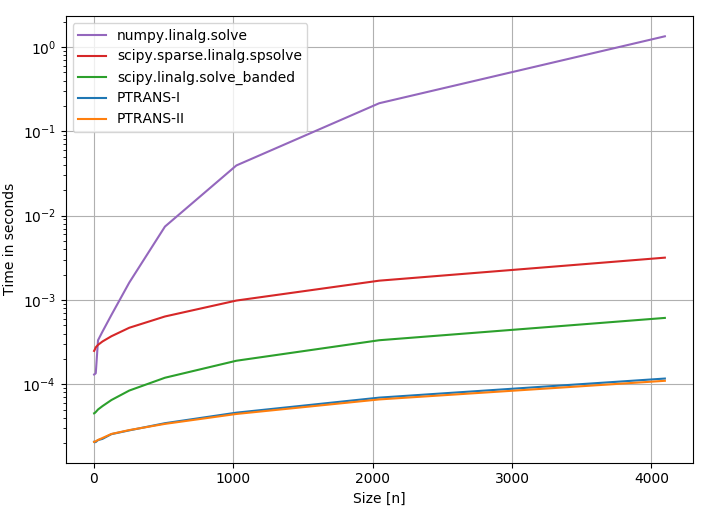
The implementations of pentapy are almost one order of magnitude faster than the scipy algorithms for banded or sparse matrices.
The performance plot was created with perfplot.
Have a look at the script: examples/03_perform_simple.py.
Requirements:
Optional
Contact
You can contact us via info@geostat-framework.org.
License
MIT © 2019 - 2023
3 maintainers
Release files for pentapy 1.4.1
For a detailed explanation of source distributions (sdists) and built distributions (wheels), please see the package formats documentation.
Source distribution (sdist)
| File | Size | Uploaded | |
|---|---|---|---|
| pentapy-1.4.1.tar.gz | 10.5 kB | Details |
Built distributions (wheels)
Total release size: 15.0 MB
Release files / pentapy-1.4.1.tar.gz
| Download URL | pentapy-1.4.1.tar.gz |
|---|---|
| Size | 10.5 kB |
| Tags | Source |
|
SHA-256 checksum How to use checksums |
d0dc6d840d9aa41ba60b6c74413bab4064b5259121627042658e66170259e9dc
|
|
BLAKE2b-256 checksum How to use checksums |
d6ad4c87b9a98ed8b9abea0a89f493a351ae3a70e44d6df9bc82354356bae07e
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-pp311-pypy311_pp73-win_amd64.whl
| Download URL | pentapy-1.4.1-pp311-pypy311_pp73-win_amd64.whl |
|---|---|
| Size | 75.5 kB |
| Tags | PyPy 3.11 PyPy 3.11 7.3 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
f670ee8e32965082372eb97125060966e67ee3148b6a69bf4b850dd2965110ae
|
|
BLAKE2b-256 checksum How to use checksums |
3b6749b6cf02feace4a34828c278674e828e635fb0affe7ecfb12c82971b4c20
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-pp311-pypy311_pp73-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-pp311-pypy311_pp73-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 88.9 kB |
| Tags | Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 PyPy 3.11 PyPy 3.11 7.3 |
|
SHA-256 checksum How to use checksums |
50590ed9cfdfb777a46dde0b0ec86aa280b7167719564c400273d7627edd7929
|
|
BLAKE2b-256 checksum How to use checksums |
f99f5b947016b9527518ba6036b2ef44cf3bcf0e4bbf9a7bbdd621f8fda15419
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-pp311-pypy311_pp73-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-pp311-pypy311_pp73-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 86.1 kB |
| Tags | Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 PyPy 3.11 PyPy 3.11 7.3 |
|
SHA-256 checksum How to use checksums |
7dc5ff5abdfee53f0efaa6e20e278bdb532301242c1c17baf65ad8b550e87b69
|
|
BLAKE2b-256 checksum How to use checksums |
8850b245193d55dc6036440261f46b8745f9963a2254717da9fec27fba940e32
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-pp311-pypy311_pp73-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-pp311-pypy311_pp73-macosx_11_0_arm64.whl |
|---|---|
| Size | 74.3 kB |
| Tags | PyPy 3.11 PyPy 3.11 7.3 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
5dd13dc83305681d45e2185121cc54f70a55cc764188075325adc4b80bfaa0d7
|
|
BLAKE2b-256 checksum How to use checksums |
5db52febec506b59d8f6ff6427b9d95e14b9620a01918525f11e2d17cdff000f
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-pp311-pypy311_pp73-macosx_10_15_x86_64.whl
| Download URL | pentapy-1.4.1-pp311-pypy311_pp73-macosx_10_15_x86_64.whl |
|---|---|
| Size | 75.2 kB |
| Tags | PyPy 3.11 PyPy 3.11 7.3 macOS 10.15+ x86-64 |
|
SHA-256 checksum How to use checksums |
4408b1d72d419561a317284ed92d10ba96ecfdcd42c2c31d6f1ecd0fd6a67fce
|
|
BLAKE2b-256 checksum How to use checksums |
795b209713f1cb7b82a07a09c2565e441c274a73578ca59de51702aeac16ef79
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-win_arm64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-win_arm64.whl |
|---|---|
| Size | 70.0 kB |
| Tags | CPython 3.14 Windows ARM64 |
|
SHA-256 checksum How to use checksums |
4a11a58829c8bd724807d9c36ec382e88f43080725406dedc3ee01b63c958fee
|
|
BLAKE2b-256 checksum How to use checksums |
ce2da2a90d839a552a3fe6691fcdbc61fa43c0c378eb6f36f84b7fa4d2f4abf8
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-win_amd64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-win_amd64.whl |
|---|---|
| Size | 82.2 kB |
| Tags | CPython 3.14 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
04ad3743424b6e69fee54e5c1ce2ecbe2b1c42240fb27710cf5e0e21192e31df
|
|
BLAKE2b-256 checksum How to use checksums |
359ede0f4cf87a24103fb443eb68cabf54b66366bba6840504782fa64e13e800
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-win32.whl
| Download URL | pentapy-1.4.1-cp314-cp314-win32.whl |
|---|---|
| Size | 69.0 kB |
| Tags | CPython 3.14 Windows x86-32 |
|
SHA-256 checksum How to use checksums |
67d135cf6e2d1dffd8f201969cb5237d209fe3bd72fdb9a4cdc8b9eb71bed2f8
|
|
BLAKE2b-256 checksum How to use checksums |
02b13646d12ba5cbf861328e6ff05705bf7790a657666b0d83867f252125d816
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-musllinux_1_2_x86_64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-musllinux_1_2_x86_64.whl |
|---|---|
| Size | 518.5 kB |
| Tags | CPython 3.14 Linux musl 1.2+ x86-64 |
|
SHA-256 checksum How to use checksums |
4f649d90f9eac532b823f9c5a7b948b34802686ae0a818bf07bc1e5ec7af3155
|
|
BLAKE2b-256 checksum How to use checksums |
14cbb87c19545dec8ecf7dcd606fb7854a190dfd6936c6b9095f2113124c7073
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-musllinux_1_2_aarch64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-musllinux_1_2_aarch64.whl |
|---|---|
| Size | 497.6 kB |
| Tags | CPython 3.14 Linux musl 1.2+ ARM64 |
|
SHA-256 checksum How to use checksums |
1c49b8bd918f1e9f1f5e7120ec88166670c36c8fde4a5464bd36bc5ede3b4ac3
|
|
BLAKE2b-256 checksum How to use checksums |
7ea761e7b5432de323664e87f4e1f18f41afb8d100c90748953b4891deb6bd62
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 519.8 kB |
| Tags | CPython 3.14 Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 |
|
SHA-256 checksum How to use checksums |
b100dd80ea8a7921dccd04386795fa80fd91ea4bb7701832ff304bb2040bbeae
|
|
BLAKE2b-256 checksum How to use checksums |
b1fd6f4742715f8081a3d4cf93c3097fafcf695bfeebdfdccd83bc492c26ca39
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 507.0 kB |
| Tags | CPython 3.14 Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 |
|
SHA-256 checksum How to use checksums |
b6b3e10cd96ab791cffebd975e49773a62fb60be10964f4d4c8e4e6afa9b3217
|
|
BLAKE2b-256 checksum How to use checksums |
07047575c5412533d7daa24e8a7014cae4117cfb53fb5b9d1b90d304232f25dc
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-macosx_11_0_arm64.whl |
|---|---|
| Size | 91.3 kB |
| Tags | CPython 3.14 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
51ede93f3e0f598020286b7dca5ff4d6e24f5e7880a1059d5dfd294257c711ca
|
|
BLAKE2b-256 checksum How to use checksums |
524a015b998a98be77dd2716a0227903dc6c7ff35c365ded88480ebdd3bfe7f1
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp314-cp314-macosx_10_15_x86_64.whl
| Download URL | pentapy-1.4.1-cp314-cp314-macosx_10_15_x86_64.whl |
|---|---|
| Size | 92.6 kB |
| Tags | CPython 3.14 macOS 10.15+ x86-64 |
|
SHA-256 checksum How to use checksums |
33b8a5a5bb9a6e61badcb92064fc21588d10def133c2fbbb3f1e0ef50482351f
|
|
BLAKE2b-256 checksum How to use checksums |
0251c8c9b16e3779ef430d8fad1df4e3250f87a2df1f1426d3d5dfc80c027bbe
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-win_arm64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-win_arm64.whl |
|---|---|
| Size | 67.8 kB |
| Tags | CPython 3.13 Windows ARM64 |
|
SHA-256 checksum How to use checksums |
13d9d2ea6fd6aa988ba09eea9bfbf5b4d8cc2d7fa6a61b8ab155b29e7d6c6a9e
|
|
BLAKE2b-256 checksum How to use checksums |
5fb8342c21efa62e63bd737370fbb3d4a855ac5860746feb99e1f535246391ae
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-win_amd64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-win_amd64.whl |
|---|---|
| Size | 79.9 kB |
| Tags | CPython 3.13 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
8cdf36271ef72396d24d800269eb2794fda2c49269db8339db68a3365e8afe78
|
|
BLAKE2b-256 checksum How to use checksums |
248020641bd140d5466e4b124feb6ba23ac1eea722679b4e7af13e51929b0b60
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-win32.whl
| Download URL | pentapy-1.4.1-cp313-cp313-win32.whl |
|---|---|
| Size | 67.3 kB |
| Tags | CPython 3.13 Windows x86-32 |
|
SHA-256 checksum How to use checksums |
dccacd3fd93b82cd401ae4ded9621292e3fac1a82a8c82f7423b236e46d1c4cd
|
|
BLAKE2b-256 checksum How to use checksums |
ea9dfaa8c6c46ee13e8fcfd03b0f0669d080c82d29c6f518a94670ce395da04c
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-musllinux_1_2_x86_64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-musllinux_1_2_x86_64.whl |
|---|---|
| Size | 522.6 kB |
| Tags | CPython 3.13 Linux musl 1.2+ x86-64 |
|
SHA-256 checksum How to use checksums |
664e2a25481e6f8b2aede38a192164bafa0d90a83101666cda35b35e50559722
|
|
BLAKE2b-256 checksum How to use checksums |
49d79fc8a8e326d393a84f976024dfa4f821c184961a25594ec499f7af3b8f34
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-musllinux_1_2_aarch64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-musllinux_1_2_aarch64.whl |
|---|---|
| Size | 499.1 kB |
| Tags | CPython 3.13 Linux musl 1.2+ ARM64 |
|
SHA-256 checksum How to use checksums |
0c9e1e32ed50a6444e2ae5269dcdce08d9fa7d27dd432068b932751399fd3761
|
|
BLAKE2b-256 checksum How to use checksums |
cd8679265cfb0ebbda8bd446004cfc314ec764845bc7faf07b7653e223b5ad64
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 525.5 kB |
| Tags | CPython 3.13 Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 |
|
SHA-256 checksum How to use checksums |
e7d4ca2b55c047530cb56e243ed494ecd108ff386202662f841970512ae58c12
|
|
BLAKE2b-256 checksum How to use checksums |
94a5e7506ef758bcf5dc6bb21a2653bc1dc81cd83a44b2f581ebbb1b30f5ac7b
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 508.6 kB |
| Tags | CPython 3.13 Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 |
|
SHA-256 checksum How to use checksums |
1cfa47e96ad79ea17349642bceeee32f477309a6e8c3e2a1234a13e9b4568e1a
|
|
BLAKE2b-256 checksum How to use checksums |
378c0084ce8b3c32997c4afb34cdf0110956e98cb924b9113d314a67ff2a4bc2
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-macosx_11_0_arm64.whl |
|---|---|
| Size | 90.5 kB |
| Tags | CPython 3.13 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
d0699c1a2f580e9abd48131da716e92f6dd31fde626029c9ae5df0f718e28199
|
|
BLAKE2b-256 checksum How to use checksums |
7f8133afba06764a3c55411bd7c4d29cb8a8a7d14975486a16ebb7aca256531f
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp313-cp313-macosx_10_13_x86_64.whl
| Download URL | pentapy-1.4.1-cp313-cp313-macosx_10_13_x86_64.whl |
|---|---|
| Size | 92.6 kB |
| Tags | CPython 3.13 macOS 10.13+ x86-64 |
|
SHA-256 checksum How to use checksums |
93823a1c6028918fe824a37e0d94a4d2d5348fe290ea3d46cc8dfc6b6dc501fe
|
|
BLAKE2b-256 checksum How to use checksums |
fec45d55fbaeb2924c469b4338050d8c37eee3d63252c55e96ad9f3202406ee4
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-win_arm64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-win_arm64.whl |
|---|---|
| Size | 67.9 kB |
| Tags | CPython 3.12 Windows ARM64 |
|
SHA-256 checksum How to use checksums |
7bd24370e4f3bd8114e6edb05d2af8b52312cba34c3a009af7c6ac500199b60a
|
|
BLAKE2b-256 checksum How to use checksums |
97723ffdb911850a516c6266e63611d920da595cfd8192ec729c71f4974f103d
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-win_amd64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-win_amd64.whl |
|---|---|
| Size | 80.1 kB |
| Tags | CPython 3.12 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
4b7a2386e8b506d5a49e008f0eb04bb837a73f070c936efbd7189730729ddcbe
|
|
BLAKE2b-256 checksum How to use checksums |
4d9934e51e07618aa16b50e1b3db3b54884518df0aed381e185ea1c95ff1c6ad
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-win32.whl
| Download URL | pentapy-1.4.1-cp312-cp312-win32.whl |
|---|---|
| Size | 67.6 kB |
| Tags | CPython 3.12 Windows x86-32 |
|
SHA-256 checksum How to use checksums |
c6a031604792e43f20aeae76d2cdfac188cde0e08007cf3696d44a45d7b27179
|
|
BLAKE2b-256 checksum How to use checksums |
28fc63d4911c0a494db00b9e6ae4532c986a361a317b7d917b4bfa55ebfd912b
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-musllinux_1_2_x86_64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-musllinux_1_2_x86_64.whl |
|---|---|
| Size | 528.2 kB |
| Tags | CPython 3.12 Linux musl 1.2+ x86-64 |
|
SHA-256 checksum How to use checksums |
851aed57116d1d2407012cfb27bdefc31b4c887f129208a39c6605bfc56738fa
|
|
BLAKE2b-256 checksum How to use checksums |
9f910863d9dd3bf31a31ebd6f004199dabe7aeb4e8d2a8c55afb92c6ef3c558f
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-musllinux_1_2_aarch64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-musllinux_1_2_aarch64.whl |
|---|---|
| Size | 505.9 kB |
| Tags | CPython 3.12 Linux musl 1.2+ ARM64 |
|
SHA-256 checksum How to use checksums |
fbbe48c85e0d8b3cbc7396c3e2cadbe1c541216bf833a5cc657c99079fb41ab5
|
|
BLAKE2b-256 checksum How to use checksums |
52a0f8ebc9afc1b9a013837e6393a4319d21fecac24a29fe5d76d554b15f6eed
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 531.0 kB |
| Tags | CPython 3.12 Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 |
|
SHA-256 checksum How to use checksums |
3da920fd8da8a2fc9ea49006a6077fd44c635fb4711a09e292c1836de7b88423
|
|
BLAKE2b-256 checksum How to use checksums |
ef0e8c4e70a033b789b5d634b67e4a6f93a89b82ae068c44daa08424cdcff173
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 517.0 kB |
| Tags | CPython 3.12 Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 |
|
SHA-256 checksum How to use checksums |
027dbad461b81f71a18be5798b2e944a8fba4e564e8184c4b0ea52f8feffc137
|
|
BLAKE2b-256 checksum How to use checksums |
de31c61a21fe66efa5e93af0f093825ee5092fb3aacf4fea14dff70ad2a61689
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-macosx_11_0_arm64.whl |
|---|---|
| Size | 91.4 kB |
| Tags | CPython 3.12 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
ffeaa3a749187ae8f2cfc4fdddbb2902264331138e3fd00f15bccb8cbfd56609
|
|
BLAKE2b-256 checksum How to use checksums |
04767ee9158c65475ae350a4f6ed04647b181784316717ff79c4a5a3534fafc2
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp312-cp312-macosx_10_13_x86_64.whl
| Download URL | pentapy-1.4.1-cp312-cp312-macosx_10_13_x86_64.whl |
|---|---|
| Size | 93.6 kB |
| Tags | CPython 3.12 macOS 10.13+ x86-64 |
|
SHA-256 checksum How to use checksums |
8c19dd70bd1e6f872f686c2f632a20fc4495079f368bd9f2f198657047a1a071
|
|
BLAKE2b-256 checksum How to use checksums |
47428e035dbf98912cf05393c7095a16bb5617e61b8edc3ce4a1f5edc90a9ee7
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-win_arm64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-win_arm64.whl |
|---|---|
| Size | 68.5 kB |
| Tags | CPython 3.11 Windows ARM64 |
|
SHA-256 checksum How to use checksums |
fe38ab0dd30f73925061314089c7dcefeba5690ebe252b68ad30ea9bc44c45d7
|
|
BLAKE2b-256 checksum How to use checksums |
c7625c6a3f0e9543d52d90ea72e881d8ad133a9fb0f286f7f2f794f6c843daa9
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-win_amd64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-win_amd64.whl |
|---|---|
| Size | 79.9 kB |
| Tags | CPython 3.11 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
a7086ff53063f15f199034252fb69096bd32212a1fe7bb5017f64fc9685117d8
|
|
BLAKE2b-256 checksum How to use checksums |
7aabf3e865e9d22133b021c67cac40f93f1b26855d1055f4703d07e651251836
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-win32.whl
| Download URL | pentapy-1.4.1-cp311-cp311-win32.whl |
|---|---|
| Size | 67.7 kB |
| Tags | CPython 3.11 Windows x86-32 |
|
SHA-256 checksum How to use checksums |
6dd26b054938e557d46125055b96ed118c0574ebe4b95aca9f361b8e5ba009d9
|
|
BLAKE2b-256 checksum How to use checksums |
e6a6f0fb90c5f21e64426468e21f7224d64faf23b3dbd6e5ba59cc6e8d4cd774
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-musllinux_1_2_x86_64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-musllinux_1_2_x86_64.whl |
|---|---|
| Size | 537.4 kB |
| Tags | CPython 3.11 Linux musl 1.2+ x86-64 |
|
SHA-256 checksum How to use checksums |
c6753d8f8aa2e4d72b2585b1036c409e4e6cc5fd31774bcee754a8575e13dffd
|
|
BLAKE2b-256 checksum How to use checksums |
4000c76c12361909ae3b694652f18cfe9a65ba6270d29bf6affd8eb8d6d4d0f2
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-musllinux_1_2_aarch64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-musllinux_1_2_aarch64.whl |
|---|---|
| Size | 517.4 kB |
| Tags | CPython 3.11 Linux musl 1.2+ ARM64 |
|
SHA-256 checksum How to use checksums |
108ec505cf630e3d4ee10441972daa4a3ec8b56a655d0c568ffbbabc61c507f5
|
|
BLAKE2b-256 checksum How to use checksums |
4b84cf438fbd73358b2b149c8e17e417718f82d3c8f7ecce119035beebe44ad3
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 532.9 kB |
| Tags | CPython 3.11 Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 |
|
SHA-256 checksum How to use checksums |
646e15fd13ecce48af8392d04a93ee9db2a683f9ded86fb37f71b603e5494d0d
|
|
BLAKE2b-256 checksum How to use checksums |
845be11805ddb6e678e68a57d4893f35a81cfa0652d0c77bb62697fc2b0a8fcf
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 524.6 kB |
| Tags | CPython 3.11 Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 |
|
SHA-256 checksum How to use checksums |
232fdbf2e40b9349360b6ef08c93fce985e26c3fc937ed09fb8c592c206eb3a4
|
|
BLAKE2b-256 checksum How to use checksums |
5e8ca0963cca79e9313de24a82c29e3a4ee8415e0e9567233e4ba0808283812f
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-macosx_11_0_arm64.whl |
|---|---|
| Size | 91.5 kB |
| Tags | CPython 3.11 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
c0cc2a4793a8e6cd6dd06d16e9a72cb9859a0dd86906f0904106f83aacc33aba
|
|
BLAKE2b-256 checksum How to use checksums |
9436d1c954b54473de04018394d6aa57579b7d20fe8dac66b823838b65d4fc4a
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp311-cp311-macosx_10_9_x86_64.whl
| Download URL | pentapy-1.4.1-cp311-cp311-macosx_10_9_x86_64.whl |
|---|---|
| Size | 93.2 kB |
| Tags | CPython 3.11 macOS 10.9+ x86-64 |
|
SHA-256 checksum How to use checksums |
4f134f02c95bba2547beadfb24a84ff4d42c5d5ea657d8235054fd607d77395f
|
|
BLAKE2b-256 checksum How to use checksums |
7725e9c079a7eddf4432e5c6555221c6839d587a5e2d5d92823ffc478ec70212
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-win_amd64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-win_amd64.whl |
|---|---|
| Size | 80.0 kB |
| Tags | CPython 3.10 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
af3f31b1288dc026b689abc6ef5ad851d14e3e615453b5916618c88b4004ef61
|
|
BLAKE2b-256 checksum How to use checksums |
83a07bb848ff3ad90980ad63875219a58c85e932f538fc1237b2876531b491d6
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-win32.whl
| Download URL | pentapy-1.4.1-cp310-cp310-win32.whl |
|---|---|
| Size | 68.1 kB |
| Tags | CPython 3.10 Windows x86-32 |
|
SHA-256 checksum How to use checksums |
17b27e5efa62d75595753c133e4dd72bb4cc90eb108c2ee1d385d2590e1a213d
|
|
BLAKE2b-256 checksum How to use checksums |
0d1672ad8f17ea127db71d1859e00f5e4dca3e0100793bd138f05c495f4089f2
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-musllinux_1_2_x86_64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-musllinux_1_2_x86_64.whl |
|---|---|
| Size | 510.3 kB |
| Tags | CPython 3.10 Linux musl 1.2+ x86-64 |
|
SHA-256 checksum How to use checksums |
d7e6832be4c15c740f59e3e411afaafbaaba902f63f980e85955ab688fe62466
|
|
BLAKE2b-256 checksum How to use checksums |
2b134bf2be1000c199c8aaf68fc2d7358f8d02e45f83b7d3df8f55dcb81936d6
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-musllinux_1_2_aarch64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-musllinux_1_2_aarch64.whl |
|---|---|
| Size | 491.0 kB |
| Tags | CPython 3.10 Linux musl 1.2+ ARM64 |
|
SHA-256 checksum How to use checksums |
644d4546f076a3b04b4079582041f6dac6edd5bb641d1c90806c2bfb54ab0a33
|
|
BLAKE2b-256 checksum How to use checksums |
77416e6f687082962168f39e1f2ca86ff8a5d1b2e95cd962bd0a7966e0fc2e84
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 506.9 kB |
| Tags | CPython 3.10 Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 |
|
SHA-256 checksum How to use checksums |
135f1676fcac9e92155c39fe3f33b70fa7ed26a57745b291f322def294141c04
|
|
BLAKE2b-256 checksum How to use checksums |
411400623b2e57d57d2bca66d7adc53ccad9b2f7baf4faabdb79df7f7ecd96e5
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 498.5 kB |
| Tags | CPython 3.10 Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 |
|
SHA-256 checksum How to use checksums |
6033f55c0ee8768b00b3980818a6afd078123c948c543478dc48d4d886f6b8f1
|
|
BLAKE2b-256 checksum How to use checksums |
c52660ed66aa0f0e8426270c4f6a91054650ea6731ba10db5a15056260a36757
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-macosx_11_0_arm64.whl |
|---|---|
| Size | 91.7 kB |
| Tags | CPython 3.10 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
194fa09f69e894cfa8c23266794150525f2d20176ef4f3f5a0b7f0e23e3d7b2e
|
|
BLAKE2b-256 checksum How to use checksums |
25b690ee233e68b9d87a3e69e261a8ae8deec911ec9a04006753f5a3dbe0188f
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp310-cp310-macosx_10_9_x86_64.whl
| Download URL | pentapy-1.4.1-cp310-cp310-macosx_10_9_x86_64.whl |
|---|---|
| Size | 93.5 kB |
| Tags | CPython 3.10 macOS 10.9+ x86-64 |
|
SHA-256 checksum How to use checksums |
d950192323b586c833c82d7f7c2f32846cd8545107cf5f0f1baf6b54fc0372a9
|
|
BLAKE2b-256 checksum How to use checksums |
6179e2178dc1ef95b75cbeb708c79ff5910c6ddb9d63b19e151e5da79d0a71a9
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-win_amd64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-win_amd64.whl |
|---|---|
| Size | 80.2 kB |
| Tags | CPython 3.9 Windows x86-64 |
|
SHA-256 checksum How to use checksums |
2aef29399f02e0d6a7bd4fd5778bfb8da327cc25e034084e8752c3bb9d125630
|
|
BLAKE2b-256 checksum How to use checksums |
367431dc68937d5ce21db9831da03b57263604f07e4efd65f1bc7e752c1e443a
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-win32.whl
| Download URL | pentapy-1.4.1-cp39-cp39-win32.whl |
|---|---|
| Size | 68.2 kB |
| Tags | CPython 3.9 Windows x86-32 |
|
SHA-256 checksum How to use checksums |
ca437e15c732a2db4105962f73a557199ca428776c5432bd74cfe6c4d1b8163b
|
|
BLAKE2b-256 checksum How to use checksums |
20dfb7cb1289b5056341d6beba377ec4ff3430de18dfdfe830e89184a7cdab17
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-musllinux_1_2_x86_64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-musllinux_1_2_x86_64.whl |
|---|---|
| Size | 509.3 kB |
| Tags | CPython 3.9 Linux musl 1.2+ x86-64 |
|
SHA-256 checksum How to use checksums |
a580d85ca8c5f97bde11b42e91f52019389520f715e38085f388fac80c225206
|
|
BLAKE2b-256 checksum How to use checksums |
8738be1c93812d385216f42dd943e574ae9388d3b5fecf3ac8c49b1294c58e2b
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-musllinux_1_2_aarch64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-musllinux_1_2_aarch64.whl |
|---|---|
| Size | 489.6 kB |
| Tags | CPython 3.9 Linux musl 1.2+ ARM64 |
|
SHA-256 checksum How to use checksums |
e7c84577031ff779a6968db70695e8366ee6d3f3037c827dd99ee3b5b9247f46
|
|
BLAKE2b-256 checksum How to use checksums |
d88737b4ab710b62302ac316518cd3bc999b08a4dd106f255de26c15982552ab
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-manylinux2014_x86_64.manylinux_2_17_x86_64.manylinux_2_28_x86_64.whl |
|---|---|
| Size | 505.9 kB |
| Tags | CPython 3.9 Linux glibc 2.17+ x86-64 Linux glibc 2.28+ x86-64 |
|
SHA-256 checksum How to use checksums |
f091dc5aa0eeec1c24857a030d0f3168d4c7c6dd210dee63928ef02f5b6be4ec
|
|
BLAKE2b-256 checksum How to use checksums |
93d75693017321d24defbcccbaac0831c7159196039335e177f08f230914be67
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-manylinux2014_aarch64.manylinux_2_17_aarch64.manylinux_2_28_aarch64.whl |
|---|---|
| Size | 497.1 kB |
| Tags | CPython 3.9 Linux glibc 2.17+ ARM64 Linux glibc 2.28+ ARM64 |
|
SHA-256 checksum How to use checksums |
6bad35dbb49689abb7cabab699695eb2e5bd81b8ed1c2ef2cc76b144e4c71697
|
|
BLAKE2b-256 checksum How to use checksums |
ca00a46fe9e3c47eacf0fadd108e3a39d94f69344876d449c6cbc830b9d0be8c
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-macosx_11_0_arm64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-macosx_11_0_arm64.whl |
|---|---|
| Size | 92.0 kB |
| Tags | CPython 3.9 macOS 11.0+ ARM64 |
|
SHA-256 checksum How to use checksums |
38d6e7aa63f570926b2abd3e1ccc7f4c797fe62693cbd3b9ff8276fbe1317b72
|
|
BLAKE2b-256 checksum How to use checksums |
fe554630155081c8e6e0134b4e747c764ff84dd74a80cdea3be0ed1c35edaf12
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
Release files / pentapy-1.4.1-cp39-cp39-macosx_10_9_x86_64.whl
| Download URL | pentapy-1.4.1-cp39-cp39-macosx_10_9_x86_64.whl |
|---|---|
| Size | 93.8 kB |
| Tags | CPython 3.9 macOS 10.9+ x86-64 |
|
SHA-256 checksum How to use checksums |
8504fd12da3f2fa08e160283e7dd92dcdd0e2a8877364f494941578209ef7b59
|
|
BLAKE2b-256 checksum How to use checksums |
4c2d69e65fff1b831bd63682f71481efcd5f6594ceb7b840f3a7e1972da87571
|
| Upload date | |
|
Uploaded using Trusted Publishing? What is trusted publishing? |
No |
| Uploaded via |
twine/6.1.0 CPython/3.13.7
|
