Mathematical graphs for Python
Project description
PGraph: graphs for Python
- GitHub repository
- Wiki (examples and details)
- Documentation
- Changelog
- Dependencies:
numpyspatialmath
This Python package allows the manipulation of directed and non-directed graphs. Also supports embedded graphs. It is suitable for graphs with thousands of nodes.
from pgraph import *
import json
# load places and routes
with open('places.json', 'r') as f:
places = json.loads(f.read())
with open('routes.json', 'r') as f:
routes = json.loads(f.read())
# build the graph
g = UGraph()
for name, info in places.items():
g.add_vertex(name=name, coord=info["utm"])
for route in routes:
g.add_edge(route[0], route[1], cost=route[2])
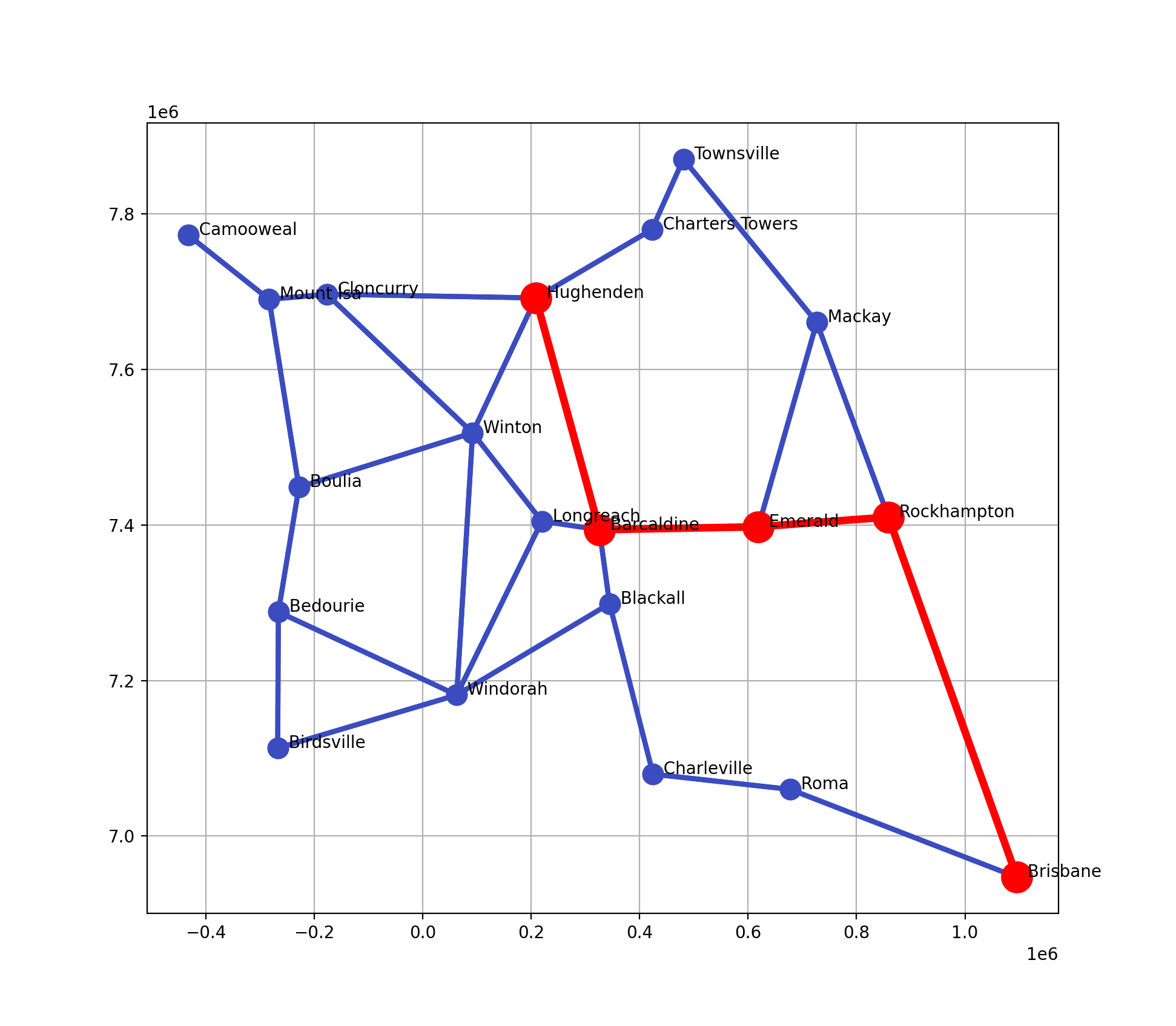
# plan a path from Hughenden to Brisbane
p = g.path_Astar('Hughenden', 'Brisbane')
g.plot(block=False) # plot it
g.highlight_path(p) # overlay the path
Properties and methods of the graph
Graphs belong to the class UGraph or DGraph for undirected or directed graphs respectively. The graph is essentially a container for the vertices.
-
g.add_vertex()add a vertex -
g.nthe number of vertices -
gis an iterator over vertices, can be used asfor vertex in g: -
g[i]reference a vertex by its index or name
-
g.add_edge()connect two vertices -
g.edges()all edges in the graph -
g.plot()plots the vertices and edges -
g.ncthe number of graph components, 1 if fully connected -
g.component(v)the component that vertexvbelongs to
-
g.path_BFS()breadth-first search -
g.path_Astar()A* search
-
g.adjacency()adjacency matrix -
g.Laplacian()Laplacian matrix -
g.incidence()incidence matrix
Properties and methods of a vertex
Vertices belong to the class UVertex (for undirected graphs) or DVertex (for directed graphs), which are each subclasses of Vertex.
v.coordthe coordinate vector for embedded graph (optional)v.namethe name of the vertex (optional)v.neighbours()is a list of the neighbouring verticesv1.samecomponent(v2)predicate for vertices belonging to the same component
Vertices can be named and referenced by name.
Properties and methods of an edge
Edges are instances of the class Edge.
Edges are not referenced by the graph object, each edge references a pair of vertices, and the vertices reference the edges. For a directed graph only the start vertex of an edge references the edge object, whereas for an undirected graph both vertices reference the edge object.
e.costcost of edge for planning methodse.next(v)vertex on edgeethat is notve.v1,e.v2the two vertices that define the edgee
Modifying a graph
g.remove(v)remove vertexve.remove()remove edgee
Subclasing pgraph classes
Consider a user class Foo that we would like to connect using a graph overlay, ie.
instances of Foo becomes vertices in a graph.
- Have it subclass either
DVertexorUVertexdepending on graph type - Then place instances of
Foointo the graph usingadd_vertexand create edges as required
class Foo(UVertex):
# foo stuff goes here
f1 = Foo(...)
f2 = Foo(...)
g = UGraph() # create a new undirected graph
g.add_vertex(f1)
g.add_vertex(f2)
f1.connect(f2, cost=3)
for f in f1.neighbours():
# say hi to the neighbours
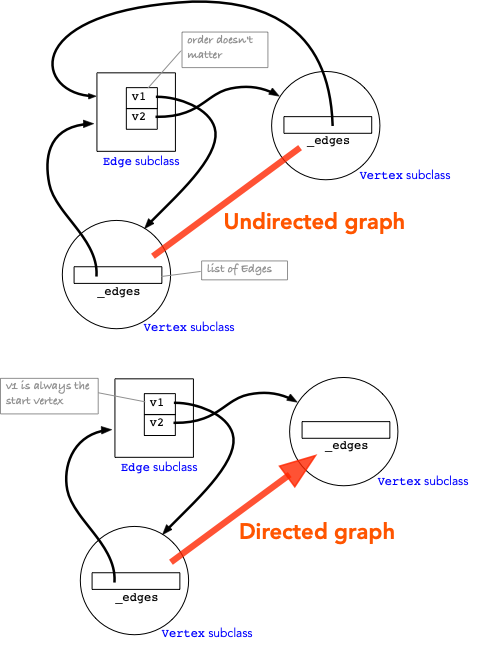
Under the hood
The key objects and their interactions are shown below.
MATLAB version
This is a re-engineered version of PGraph.m which ships as part of the Spatial Math Toolbox for MATLAB. This class is used to support bundle adjustment, pose-graph SLAM and various planners such as PRM, RRT and Lattice.
The Python version was designed from the start to work with directed and undirected graphs, whereas directed graphs were a late addition to the MATLAB version. Semantics are similar but not identical. In particular the use of subclassing rather than references to user data is encouraged.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file pgraph_python-0.6.3.tar.gz.
File metadata
- Download URL: pgraph_python-0.6.3.tar.gz
- Upload date:
- Size: 22.6 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.0.1 CPython/3.10.16
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
ff41f718daf7ae925d36cd7d17f567b67479f115f073f497f985733ecbbc90b4
|
|
| MD5 |
48b50e270c1b475eb6ba858fe7cbb50e
|
|
| BLAKE2b-256 |
637f89b04d2bfbb0e46a08a93c51b63d96a7be32d0b861021e9db533762ba356
|
File details
Details for the file pgraph_python-0.6.3-py3-none-any.whl.
File metadata
- Download URL: pgraph_python-0.6.3-py3-none-any.whl
- Upload date:
- Size: 17.7 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.0.1 CPython/3.10.16
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
184d51b5acc595daceb92d9505d614ec9b72539d37e3162cbe6fc880d6d1d807
|
|
| MD5 |
2283d7de54b2abbe2c8a3b2bee6f42f1
|
|
| BLAKE2b-256 |
a1a4b7c6b1971bdff95429a52e60ab04c21d9176307d36299a07d0076fa63b1b
|