pwlf 1.1.7

fit piecewise linear functions to data

About

A library for fitting continuous piecewise linear functions to data. Just specify the number of line segments you desire and provide the data.

Check out the documentation!

Read the blog post.

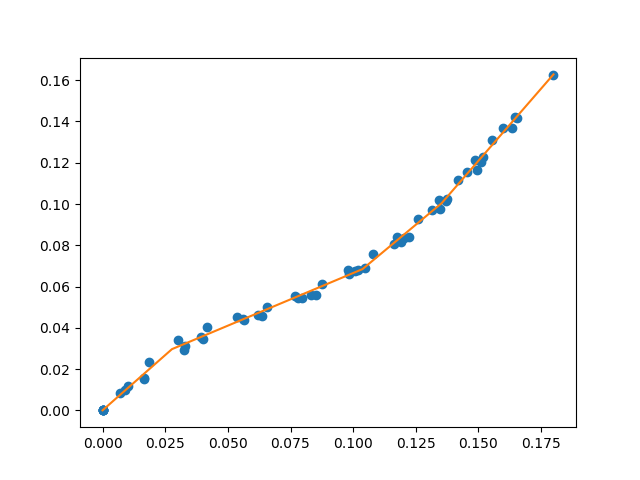
Example of a continuous piecewise linear fit to data.

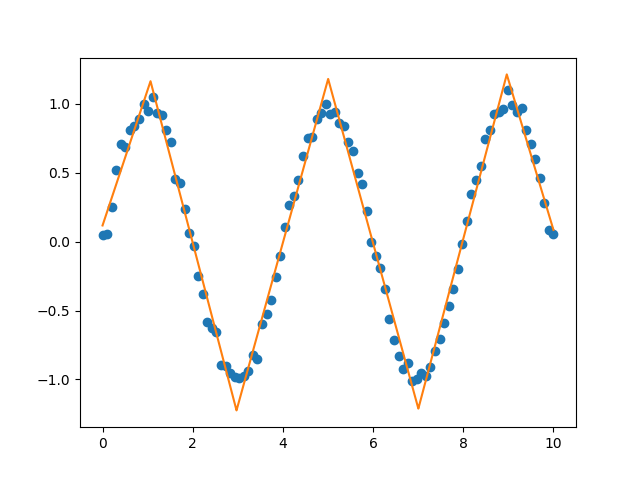
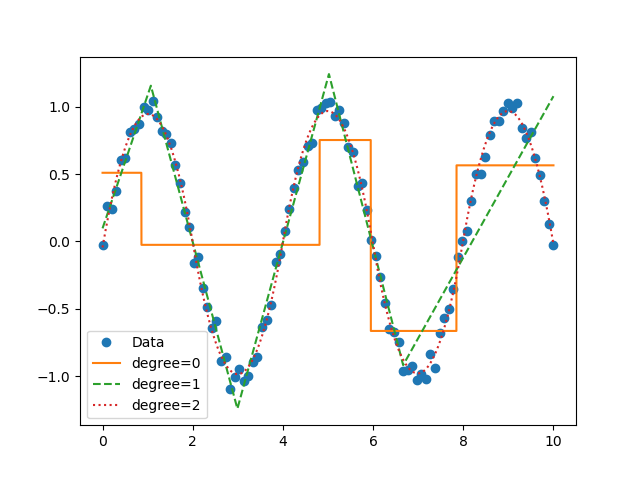
Example of a continuous piecewise linear fit to a sine wave.

Now you can perform segmented constant fitting and piecewise polynomials!

Features

For a specified number of line segments, you can determine (and predict from) the optimal continuous piecewise linear function f(x). See this example.

You can fit and predict a continuous piecewise linear function f(x) if you know the specific x locations where the line segments terminate. See this example.

If you want to pass different keywords for the SciPy differential evolution algorithm see this example.

You can use a different optimization algorithm to find the optimal location for line segments by using the objective function that minimizes the sum of square of residuals. See this example.

Instead of using differential evolution, you can now use a multi-start gradient optimization with fitfast() function. You can specify the number of starting points to use. The default is 2. This means that a latin hyper cube sampling (space filling DOE) of 2 is used to run 2 L-BFGS-B optimizations. See this example which runs fit() function, then runs the fitfast() to compare the runtime differences!

Installation

You can now install with pip.

[sudo] pip install pwlf

Or clone the repo

git clone https://github.com/cjekel/piecewise_linear_fit_py.git

then install with pip

[sudo] pip install ./piecewise_linear_fit_py

How it works

This paper explains how this library works in detail.

This is based on a formulation of a piecewise linear least squares fit, where the user must specify the location of break points. See this post which goes through the derivation of a least squares regression problem if the break point locations are known. Alternatively check out Golovchenko (2004).

Global optimization is used to find the best location for the user defined number of line segments. I specifically use the differential evolution algorithm in SciPy. I default the differential evolution algorithm to be aggressive, and it is probably overkill for your problem. So feel free to pass your own differential evolution keywords to the library. See this example.

Changelog

All changes now stored in CHANGELOG.md

New degree= keyword allows you to fit segmented constants or piecewise polynomials! Now you can calculate standard error and p-values for the non-linear regression problem!

Requirements

Python 2.7+

NumPy (Tested on version >= 1.14.0)

SciPy (Tested on version >= 1.2.0)

pyDOE (Tested on version >= 0.3.8)

setuptools >= 38.6.0

Optional:

TensorFlow (Versions < 2.0.0)

License

MIT License

Citation

@Manual{pwlf,
    author = {Jekel, Charles F. and Venter, Gerhard},
    title = {{pwlf:} A Python Library for Fitting 1D Continuous Piecewise Linear Functions},
    year = {2019},
    url = {https://github.com/cjekel/piecewise_linear_fit_py}
}