A package for studying the arc diagrams of mathematical knots
Project description
PyArcKnot
PyArcKnot is a package for studying the arc diagrams of mathematical knots.
It was developed as part of my Final Project for my Industrial Design Engineering Degree, with the help and support of Pedro González Manchón. The Final Project paper (in Spanish) can be found here.
The following is just a showcase of some of the most important functions. For a more in-depth demonstration of the possibilities available, check out the Jupyter Notebook demo.
The package requires NumPy, Matplotlib, Sympy and Numba. They can be installed by running:
pip install numpy matplotlib sympy numba
To install the PyArcKnot package run:
pip install pyarcknot
The package consists of 4 modules:
import pyarcknot.knot_matrix as km
import pyarcknot.knot_diagram as kd
import pyarcknot.knot_calculate as kc
import pyarcknot.turaev_surface as ts
Knot Matrix
Knot Matrix is used to define the knot diagrams as NumPy arrays in order to be able to work with them
k8_21_arc = km.clean_k_arc('2 7 1 4 3 5 4 8 2 6 1 5 3 7 6 8')
k8_21_xco = km.xco_arc(k8_21_arc)
print(k8_21_xco)
[[0 0 0 0 0 1 0 2]
[0 0 1 0 0 3 2 0]
[1 0 3 0 2 0 0 0]
[0 1 3 0 3 2 0 0]
[0 0 0 2 3 0 3 1]
[0 0 2 3 1 0 0 0]
[2 3 0 1 0 0 0 0]
[0 2 0 0 0 0 1 0]]
Knot Diagram
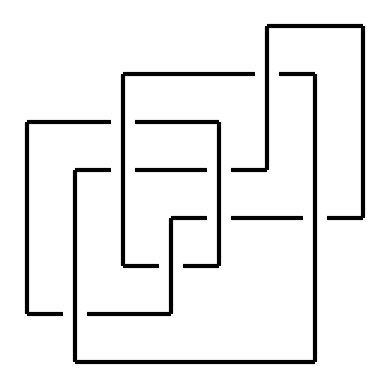
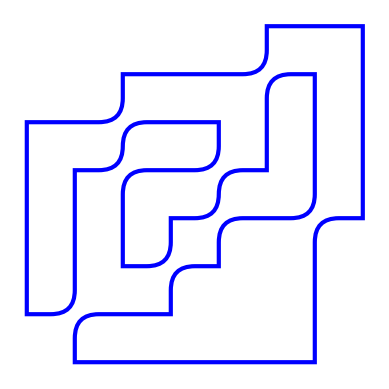
Knot Diagram uses Matplotlib to display diagrams of the knot.
kd.draw_arc(k8_21_xco)
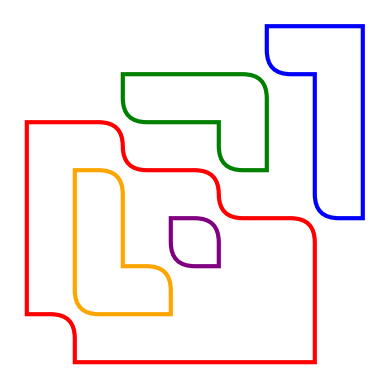
It can also return the number of loops in a smoothed diagram
kd.draw_diagrams(k8_21_xco)
Number of crossings = 8
|s_A D| = 5
|s_B D| = 1
Knot Calculate
Knot Calculate is used to calculate properties of the diagram such as the Kauffman Bracket Polynomial or the Jones Polynomial. For this, Sympy was used to work with polynomials and Numba to increase the performance and reduce the calculation time.
kc.kauffman_bracket(k8_21_xco)
$\displaystyle A^{16} - 2 A^{12} + 2 A^{8} - 3 A^{4} + 3 - \frac{2}{A^{4}} + \frac{2}{A^{8}}$
kc.jones_polynomial(k8_21_xco)
$\displaystyle \frac{2}{t} - \frac{2}{t^{2}} + \frac{3}{t^{3}} - \frac{3}{t^{4}} + \frac{2}{t^{5}} - \frac{2}{t^{6}} + \frac{1}{t^{7}}$
Turaev Surface
Turaev Surface uses Matplotlib to render a 3D surface obtained from the diagram of the knot.
ts.turaev_surf(k8_21_xco)
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file pyarcknot-0.0.2.tar.gz.
File metadata
- Download URL: pyarcknot-0.0.2.tar.gz
- Upload date:
- Size: 10.5 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.4
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
2b265a02183365cc6ad5407d0e925f24c8c87a6a8685072b37fadafc3d4e6b96
|
|
| MD5 |
cc93e06afec0a52449dd96665cfb2f9b
|
|
| BLAKE2b-256 |
1f2dc36810b1507e3a2b0f7ffec5cfc89b16de69370ce1acb331158d90452fa5
|
File details
Details for the file pyarcknot-0.0.2-py3-none-any.whl.
File metadata
- Download URL: pyarcknot-0.0.2-py3-none-any.whl
- Upload date:
- Size: 10.7 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.4
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
6758eadcf34acad7aac3473875f38c2a844a9f10ea767cc02889ed4c6d9be3bb
|
|
| MD5 |
bd0e08cf5aa9d9fbb4b722642fc8649d
|
|
| BLAKE2b-256 |
4591bad1f8e03edbd95a5e50c8e95ddcd32cf698dd961a6cda4ac19d8d8f233d
|