cut pursuit algorithms
Project description
Cut-Pursuit Algorithms, Parallelized Along Components (fork)
About this fork
The original code in available in this repository. https://gitlab.com/1a7r0ch3/parallel-cut-pursuit.
This a fork for python packaging purposes.
Please post issues in this repos only if you are sure your problem is related to the packaging... and please post issue on the upstream repository only if you are sure your problem is not related to the packaging.
See below the original README (only the python section was modified)
Original README
Generic C++ classes for implementing cut-pursuit algorithms.
Specialization to convex problems involving graph total variation, and nonconvex problems involving contour length, as explained in our articles (Landrieu and Obozinski, 2016; Raguet and Landrieu, 2018).
Parallel implementation with OpenMP.
MEX interfaces for GNU Octave or Matlab.
Extension modules for Python.
This Git repository uses submodules.
Clone with
git clone --recurse-submodules https://gitlab.com/1a7r0ch3/parallel-cut-pursuit
Pull changes with
git pull --recurse-submodules
Table of Contents
- General problem statement
- C++ classes and Specializations
2.1. Proximity operator of the graph total variation
2.2. Quadratic functional and graph total variation
2.3. Separable multidimensional loss and graph total variation
2.4. Separable distance and contour length - Documentation
3.1. Directory tree
3.2. Graph structure
3.3. C++ documentation
3.4. GNU Octave or Matlab
3.5. Python - References
- License
General problem statement
The cut-pursuit algorithms minimize functionals structured, over a weighted graph G = (V, E, w), as
F: x ∈ ΩV ↦ f(x) + ∑(u,v) ∈ E w(u,v) ψ(xu, xv) ,
where Ω is some base set, and the functional ψ: Ω² → ℝ penalizes dissimilarity between its arguments, in order to enforce solutions which are piecewise constant along the graph G.
The cut-pursuit approach is to seek partitions V of the set of vertices V, constituting the constant connected components of the solution, by successively solving the corresponding problem, structured over the reduced graph G = (V, E), that is
arg minξ ∈ ΩV F(x) , such that ∀ U ∈ V, ∀ u ∈ U, xu = ξU ,
and then refining the partition.
A key requirement is thus the ability to solve the reduced problem, which often have the exact same structure as the original one, but with much less vertices |V| ≪ |V|. If the solution of the original problem has only few constant connected components in comparison to the number of vertices, the cut-pursuit strategy can speed-up minimization by several orders of magnitude.
Cut-pursuit algorithms come in two main flavors, namely “directionally differentiable” and “noncontinuous”.
-
In the directionally differentiable case, the base set Ω is typically a vector space, and it is required that f is differentiable, or at least that its nondifferentiable part is separable along the graph and admits (potentially infinite) directional derivatives. This comprises notably many convex problems, where ψ(xu, xv) = ║xu − xv║, that is to say involving a graph total variation. The refinement of the partition is based on the search for a steep directional derivative, and the reduced problem is solved using convex or continuous optimization; optimality guarantees can be provided.
-
In the noncontinuous case, the dissimilarity penalization typically uses ψ(xu, xv) = 0 if xu =xv, 1 otherwise, resulting in a measure of the contour length of the constant connected components. The functional f is typically required to be separable along the graph, and to have computational properties favorable enough for solving reduced problems. The refinement of the partition relies on greedy heuristics.
Both flavors admit multidimensional extensions, that is to say Ω is not required to be only a set of scalars.
C++ classes and Specializations
The module maxflow implements the class Maxflow, a modification of the Graph class of Y. Boykov and V. Kolmogorov, for making use of their maximum flow algorithm.
The module cut_pursuit implements the base class Cp, defining all steps of the cut-pursuit approach in virtual methods.
The module cut_pursuit_d1 implements the class Cp_d1 derived from Cp, specializing cut-pursuit for directionally differentiable cases involving the graph total variation.
The module cut_pursuit_d0 implements the class Cp_d0 derived from Cp, specializing cut-pursuit for noncontinuous cases involving the contour length penalization.
Cp_prox_tv: proximity operator of the graph total variation
Also coined “graph total variation denoising” or “general fused LASSO signal approximation”. The objective functional is
F: x ∈ ℝD⨯V ↦ 1/2 ║y − x║Mℓ2 + ∑(u,v) ∈ E w(u,v) ║xu − xv║p, Mδ ,
where D is the dimension of the signal on each vertex, y ∈ ℝD⨯V, Mℓ is a diagonal metric weighting the square ℓ2 norm, w ∈ ℝE are regularization weights, and the norm on the finite differences is defined by p being 1 or 2 and a weighting diagonal metric Mδ.
The reduced problem is solved using the preconditioned forward-Douglas–Rachford splitting algorithm, included as a git submodule pcd-prox-split.
Cp_d1_ql1b: quadratic functional, ℓ1 norm, bounds, and graph total variation
The base set is Ω = ℝ, and the general form is
F: x ∈ ℝV ↦
1/2 ║y(ℓ2) − Ax║2 +
∑v ∈ V λv
|y(ℓ1) − xv| +
∑v ∈ V
ι[mv, Mv](xv) +
∑(u,v) ∈ E w(u,v)
|xu − xv| ,
where y(ℓ2) ∈ ℝn, A: ℝV → ℝn is a linear operator, y(ℓ1) ∈ ℝV and λ ∈ ℝV and w ∈ ℝE are regularization weights, m, M ∈ ℝV are parameters and ι[a,b] is the convex indicator of [a, b] : x ↦ 0 if x ∈ [a, b], +∞ otherwise.
When y(ℓ1) is zero, the combination of ℓ1 norm and total variation is sometimes coined fused LASSO.
When A is the identity, λ is zero and there are no box constraints, the problem boils down to the proximity operator of the graph total variation.
Currently, A must be provided as a matrix. See the documentation for special cases.
The reduced problem is solved using the preconditioned forward-Douglas–Rachford splitting algorithm, included as a git submodule pcd-prox-split.
An example with GNU Octave or Matlab and Python interfaces, where A is a full ill-conditioned matrix, with positivity and fused LASSO constraints, on a task of brain source identification from electroencephalography.
| ground truth | raw retrieved activity | identified sources | ||||
 |
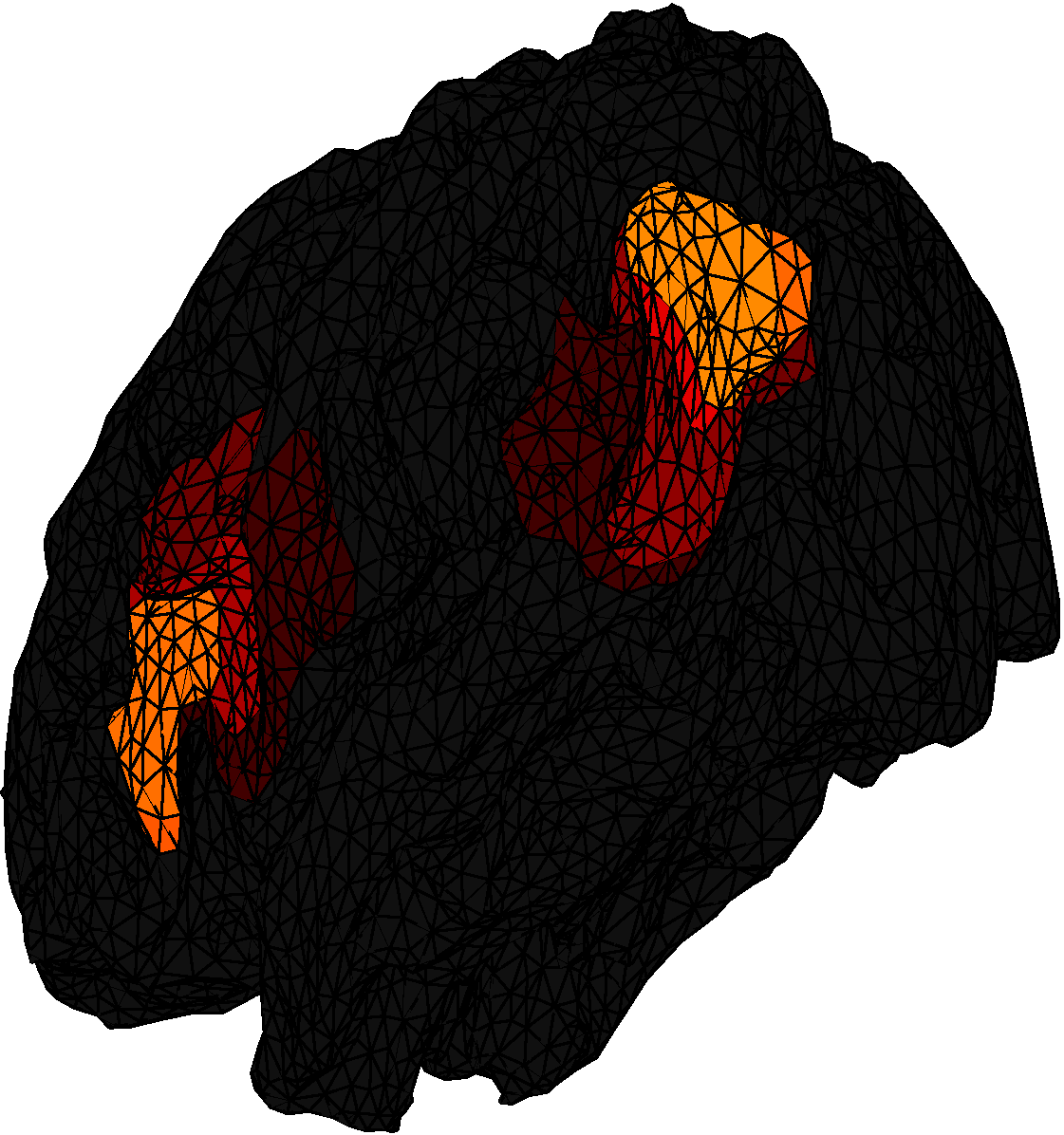 |
 |
Cp_d1_lsx: separable loss, simplex constraints, and graph total variation
The base set is Ω = ℝD, where D can be seen as a set of labels, and the general form is
F: x ∈ ℝD⨯V ↦ f(y, x) +
∑v ∈ V ιΔD(xv) +
∑(u,v) ∈ E w(d1)(u,v)
∑d ∈ D λd |xu,d − xv,d| ,
where y ∈ ℝD⨯V, f is a loss functional (see below), w(d1) ∈ ℝE and λ ∈ ℝD are regularization weights, and ιΔD is the convex indicator of the simplex ΔD = {x ∈ ℝD | ∑d xd = 1 and ∀ d, xd ≥ 0}: x ↦ 0 if x ∈ ΔD, +∞ otherwise.
The following loss functionals are available, where w(f) ∈ ℝV are weights on vertices.
Linear: f(y, x) = − ∑v ∈ V w(f)v ∑d ∈ D xv,d yv,d
Quadratic: f(y, x) = ∑v ∈ V w(f)v ∑d ∈ D (xv,d − yv,d)2
Smoothed Kullback–Leibler divergence (equivalent to cross-entropy):
f(y, x) = ∑v ∈ V w(f)v
KL(α u + (1 − α) yv, α u + (1 − α) xv),
where α ∈ ]0,1[,
u ∈ ΔD is the uniform discrete distribution over D,
and
KL: (p, q) ↦ ∑d ∈ D pd log(pd/qd).
The reduced problem is solved using the preconditioned forward-Douglas–Rachford splitting algorithm, included as a git submodule pcd-prox-split.
An example with the smoothed Kullback–Leibler is provided with GNU Octave or Matlab and Python interfaces, on a task of spatial regularization of semantic classification of a 3D point cloud.
| ground truth | random forest classifier | regularized classification | ||||
 |
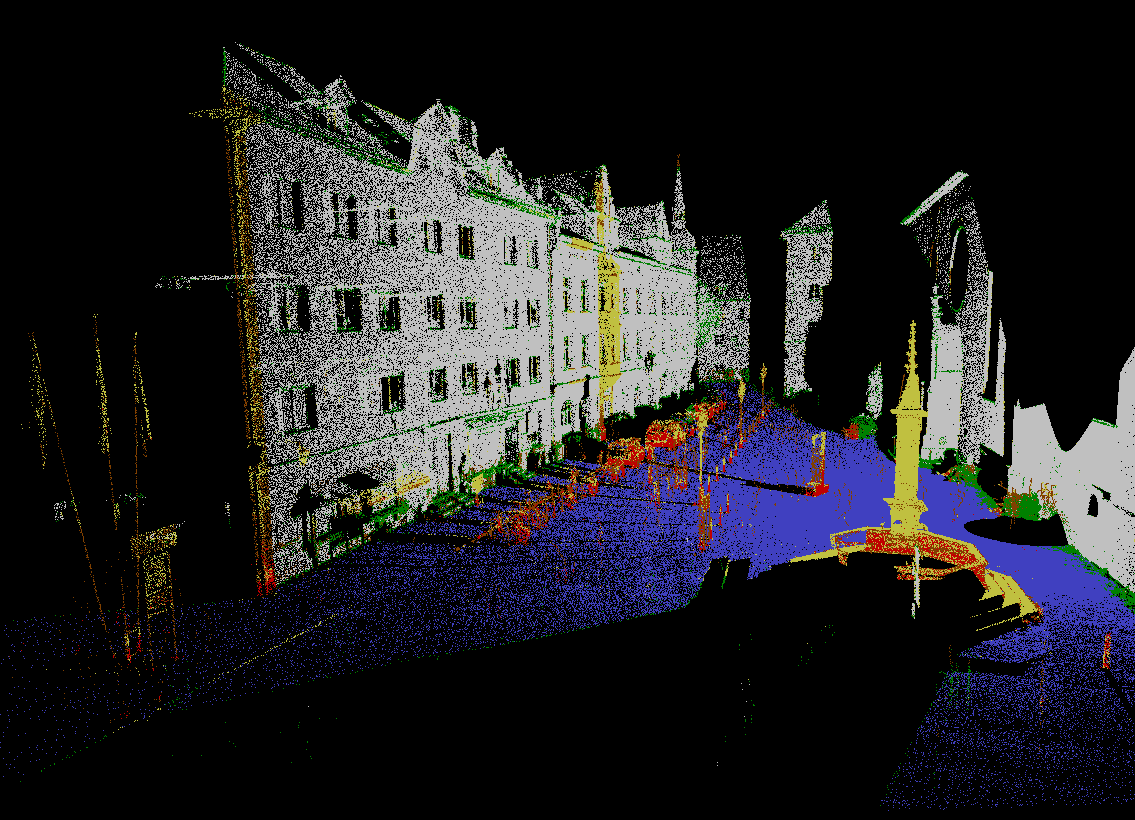 |
 |
Cp_d0_dist: separable distance and weighted contour length
The base set is Ω = ℝD or ΔD and the general form is
F: x ∈ ℝD⨯V ↦ f(y, x) + ∑(u,v) ∈ E w(d0)(u,v) ║xu − xv║0 ,
where y ∈ ΩV, f is a loss functional akin to a distance (see below), and ║·║0 is the ℓ0 pseudo-norm x ↦ 0 if x = 0, 1 otherwise.
The following loss functionals are available, where w(f) ∈ ℝV are weights on vertices and m(f) ∈ ℝD are weights on coordinates.
Weighted quadratic: Ω = ℝD and
f(y, x) = ∑v ∈ V w(f)v ∑d ∈ D m(f)d (xv,d − yv,d)2
Weighted smoothed Kullback–Leibler divergence (equivalent to cross-entropy):
Ω = ΔD and
f(y, x) = ∑v ∈ V w(f)v
KLm(f)(α u + (1 − α) yv, α u + (1 − α) xv),
where α ∈ ]0,1[,
u ∈ ΔD is the uniform discrete distribution over D,
and
KLm(f): (p, q) ↦ ∑d ∈ D m(f)d pd log(pd/qd).
The reduced problem amounts to averaging, and the split step uses k-means++ algorithm.
When the loss is quadratic, the resulting problem is sometimes coined “minimal partition problem”.
An example with the smoothed Kullback–Leibler is provided with GNU Octave or Matlab interface, on a task of spatial regularization of semantic classification of a 3D point cloud.
Documentation
Directory tree
.
├── include/ C++ headers, with some doc
├── octave/ GNU Octave or Matlab code
│ ├── doc/ some documentation
│ └── mex/ MEX C++ interfaces
├── pcd-prox-split/ git submodule preconditionned forward-Douglas–Rachford
│ algorithm (required only for directionnaly
│ differentiable cases and example data)
├── python/ Python code
│ ├── cpython/ C Python interfaces
│ └── wrappers/ python wrappers and documentation
├── src/ C++ sources
└── wth-element/ git submodule for weighted quantiles search
(required only for cp_d1_ql1b)
C++ documentation
Requires C++11.
Be sure to have OpenMP enabled with your compiler to enjoy parallelization. Note that, as of 2020, MSVC still does not support OpenMP 3.0 (published in 2008); consider switching to a decent compiler.
The number of parallel threads used in parallel regions is crucial for good performance; it is roughly controlled by a preprocessor macro MIN_OPS_PER_THREAD which can be again set with-D compilation flag. A rule of thumb is to set it to 10000 on personal computers with a handful of cores, and up to 100000 for large computer clusters with tens of cores.
The C++ classes are documented within the corresponding headers in include/.
Graph structure
Graph structures must be given as forward-star representation. For conversion from simple adjacency list representation, or for creation from scratch for regular N-dimensionnal grids (2D for images, 3D for volumes, etc.), see the pcd-prox-split/grid-graph git submodule.
GNU Octave or Matlab
See the script compile_parallel_cut_pursuit_mex.m for typical compilation commands; it can be run directly from the GNU Octave interpreter, but Matlab users must set compilation flags directly on the command line CXXFLAGS = ... and LDFLAGS = ....
The integer type holding the components assignment is by defaut on 16 bits. For applications expecting a large number of components, this can be extended to 32 bits with the compilation option -DCOMP_T_ON_32_BITS.
Extensive documentation of the MEX interfaces can be found within dedicated .m files in octave/doc/.
The script example_prox_tv.m exemplifies the use of Cp_prox_tv, on a task of color image denoising.
The script example_EEG.m exemplifies the use of Cp_d1_ql1b, on a task of brain source identification from electroencephalography.
The scripts example_labeling_3D.m and example_labeling_3D_d0.m exemplify the use of, respectively, Cp_d1_lsx and Cp_d0_dist, on a task of spatial regularization of semantic classification of a 3D point cloud.
Python
Requires numpy package.
See the script setup.py for compiling modules with setuptools; it can be run simply by using pip
e.g. python -m pip install .. pre compiled binaries for Windows and Linux will soon be available on PyPI.
if more than 65535 components are expected in you graph you can force the use of 32 bit indices by setting
the COMP_T_ON_32_BITS environement variable to 1 e.g. export COMP_T_ON_32_BITS=1 on bash.
Extensive documentation of the Python wrappers can be found in the corresponding .py files.
The script example_prox_tv.py exemplifies the use of Cp_prox_tv, on a task of color image denoising.
The script example_EEG.py exemplifies the use of Cp_d1_ql1b, on a task of brain source identification from electroencephalography.
The scripts example_labeling_3D.py and example_labeling_3D_d0.py exemplify the use of, respectively, Cp_d1_lsx and Cp_d0_dist, on a task of spatial regularization of semantic classification of a 3D point cloud.
References
L. Landrieu and G. Obozinski, Cut Pursuit: Fast Algorithms to Learn Piecewise Constant Functions on Weighted Graphs, 2017.
H. Raguet and L. Landrieu, Cut-pursuit Algorithm for Regularizing Nonsmooth Functionals with Graph Total Variation, 2018.
Y. Boykov and V. Kolmogorov, An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004.
License
This software is under the GPLv3 license.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distributions
Hashes for pycut_pursuit-0.1.3-cp312-cp312-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ca039b18b6599f807c9979bbcf0ff0a8edbfdc44c81b6380343dc6e33c327cde |
|
| MD5 | 35f467f7a3ec1b670292d05661a354a3 |
|
| BLAKE2b-256 | 0f3f157d531c5e822d2f97fcf554bf780718c2a528c7fa665042bb5200dc50d0 |
Hashes for pycut_pursuit-0.1.3-cp312-cp312-musllinux_1_1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 97e79137fd47460f4f6ae64ae3d30c87c3d405d315f6e8c06bb0f7960cb34248 |
|
| MD5 | 93fbc23e2640fc96a4646aac18089745 |
|
| BLAKE2b-256 | 23edc1eb467fbc0aa1d394af3dc6cc1b3c403b3a260d1552fe70547bec29d0b0 |
Hashes for pycut_pursuit-0.1.3-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 3670da22fb973e5e5c480f19e447c3ef1918bf63be760a028ce40417af45cb2c |
|
| MD5 | 0910003e46b093de193dee7131cbe6c6 |
|
| BLAKE2b-256 | 615f49f37f6a540917d2a887977b65661d3486222d384f4d39669ced8c928c93 |
Hashes for pycut_pursuit-0.1.3-cp312-cp312-macosx_14_0_arm64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 8b73c930472878d08b3d58278fdd4f28d2495e7fe760d4a5127232d1c69f710b |
|
| MD5 | a9ffc574d68f0146c51c08726fbff885 |
|
| BLAKE2b-256 | b4f1e4e4d4885ace3baeb37fbbac7af06bd5706327ad16dbea047b440f754361 |
Hashes for pycut_pursuit-0.1.3-cp312-cp312-macosx_11_0_arm64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 7db9f5ef373e977d35097786f7b5c6e6dc0673f8a7af41ec8fdff3f2d4355f3e |
|
| MD5 | 71608da8e1c608d7d4c3da8ab13ededf |
|
| BLAKE2b-256 | 9180a99d7071efc508ed9f15f129d132b0dcb5ea1f0878c9a027a997b4dadad8 |
Hashes for pycut_pursuit-0.1.3-cp311-cp311-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | af95b2dc513a03d1f15ccebf91101ea923eecb456d998a9da9862dac76044f64 |
|
| MD5 | 0d522562ba35b79d95fe29e96a3dacf8 |
|
| BLAKE2b-256 | b30e684da6a65f65600afd4861fdee9ccf8de770d551ba19e19f405d655a9bcd |
Hashes for pycut_pursuit-0.1.3-cp311-cp311-musllinux_1_1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 6eaf379d4a9ad41b1ccf498496cdabe0e764bcfa9b34e1ddcfcd04be98e3f112 |
|
| MD5 | e171ee5b3832ce0974ae7e98f619cae8 |
|
| BLAKE2b-256 | 9b73bdc49941e8dc59133b90c1a978baaa751f3c5022b87cc3dbc961df7971cf |
Hashes for pycut_pursuit-0.1.3-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 67b79e11a99b69e11e67eb408d2494663bd4ad224d9148f6e75fc02b44338347 |
|
| MD5 | 438c958ed2090874b292a78242f6840a |
|
| BLAKE2b-256 | b766c4d6e259986dd7e4864ae9c704fc1c5a594c89803b467f9efc284a5fe919 |
Hashes for pycut_pursuit-0.1.3-cp311-cp311-macosx_11_0_arm64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 94b5a69f85074817625a7e4836b5e63c5d500b294e92dd94bbc5dc7e3421e75e |
|
| MD5 | c4622e16763e3a59f1d9532f5e42440c |
|
| BLAKE2b-256 | c359f92ba775bbe79c6ec54d7fba8e4c5fa2b88a7ff91112849d5795d1ae0912 |
Hashes for pycut_pursuit-0.1.3-cp310-cp310-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | aefbfe5c121a6195c6b6a0f367e03a8bf9fccf0d34250a52ba245ecdffa194db |
|
| MD5 | d9d12441032fe236e62dd88ae3c42b18 |
|
| BLAKE2b-256 | 6ca47cef6f018a993f4542fa375f8a228bdb9a7d1cc3bfb98d45b0138881d5da |
Hashes for pycut_pursuit-0.1.3-cp310-cp310-musllinux_1_1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 46e4fa40a31b6213799c76d9ba4262570c8250365f6951b4ea87bd0f0b9ccad3 |
|
| MD5 | d413f180199c862ba347c09547f50bd5 |
|
| BLAKE2b-256 | 17eda56e4def9645ec5e8218f003922135529da9e3e9a1ca1053bd6b29be71e7 |
Hashes for pycut_pursuit-0.1.3-cp310-cp310-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 35bea9b0ac0d227e1461cc851a05ad1bab5b6d62e14a57b30a6768fbbfa573e9 |
|
| MD5 | 262599aac53fe18101bf283cc91aaab5 |
|
| BLAKE2b-256 | 7aedc150f7ae686ae423555e1b36a94d3547fb0477d02868e1b17a5039f03486 |
Hashes for pycut_pursuit-0.1.3-cp310-cp310-macosx_11_0_arm64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 74a69ecc5d9685e2a4e98fd037e46fc1c0b932e00ac75fbc85e82bb47a24144b |
|
| MD5 | dc1b637e379d3f02e3572933a9054c10 |
|
| BLAKE2b-256 | d0816a7edcceb2b63ecd68fe3a6e924361589a7f84043ea5207d42101b2a15de |
Hashes for pycut_pursuit-0.1.3-cp39-cp39-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 35f0af2ca9d0affbb361a76953cc651b3037b2cae3c29d43add8e7947ed707ef |
|
| MD5 | 2358dde33f1ad860a829a487679baf15 |
|
| BLAKE2b-256 | 4746a7f3a8bd383d53438dcc38480b01df2f34b29bf9b5865fcf6a48148bd562 |
Hashes for pycut_pursuit-0.1.3-cp39-cp39-musllinux_1_1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | f44acd6c5f417dc2836baf3c805e1e5c55f13264964196fd3f325c8354fdb31f |
|
| MD5 | 0abaed7860ea914892322067c1e30c81 |
|
| BLAKE2b-256 | 4b22c8b62847c2c722e7f88f9cffa9bdd272ea0ecc9ebbe6a68225a15e4308d0 |
Hashes for pycut_pursuit-0.1.3-cp39-cp39-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 4d587ee4207a48a1f4d1269c9595ffdb32ccb723ae46ad645193d7c7eabf7850 |
|
| MD5 | 84079a33616cc36a19496cd8dbd3749f |
|
| BLAKE2b-256 | d635a362e779b44b332edc835fd4f3ca5423e0953e7e21163d268cdcd61272df |
Hashes for pycut_pursuit-0.1.3-cp39-cp39-macosx_11_0_arm64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 0dd577efe130ba04364bae892a6c3fb8e15fa263d7f05726f1bfc9f8e990b188 |
|
| MD5 | db7984f715967e056633eb12c45be7ad |
|
| BLAKE2b-256 | 2570bc2090252334d3bbd06b84b0023deba0bbebc60dd3ceb1e99d7e77a15ed6 |











