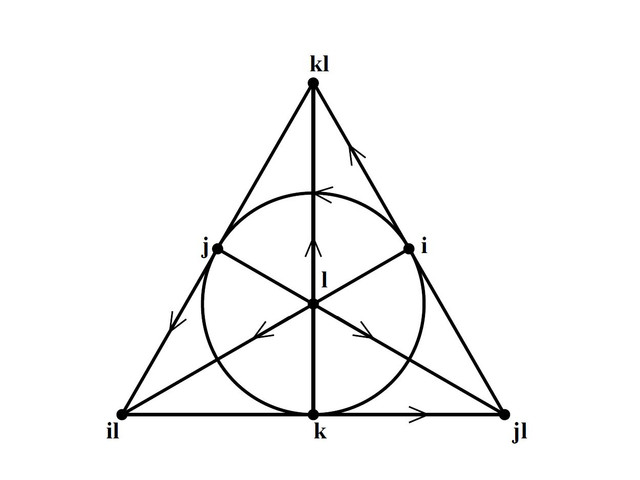
Octonion Number System
Project description
pyoctonion
Octonion in Python
Authors: Charith Atapattu & Kalpa Thudewaththage
In this project, we introduce Python Library for octonions. There is a Python Library for facilitating algebra in quaternions called "pyquaternion". However, no python Library for doing algebraic operations in octonions. We introduce this "pyoctonion" library for researchers who need calculations in octonions. Due to lack of commutativity and Associativity, manual simpliflication is always time consuming and might go wrong. This package will certainly help to check octonionic identities and work with wide range of problems in octonions.
Installation
Install from PyPI Please visit the pyoctonion homepage for full information and the latest documentation. Designed for Python 2.7+ and 3.0+
$ pip install pyoctonion
Quick Start
Run the following for a basic overview. A copy of this example can be found in demo.ipynb.
Basic Usage
In your code, simply import the Octonion object from the pyoctonion module:
from pyoctonion import Octonion
Octonion Features
Define Octonion objects
Define a,b,c Octonions.
a = Octonion(1,2,3,4,5,6,7,8)
b = Octonion(1,3,5,7,9,2,4,6)
c = Octonion(8,7,6,5,4,3,2,1)
#printing octonion objects values
print(a)
print(b)
print(c)
output
+1.0000 +2.0000i +3.0000j +4.0000k +5.0000l +6.0000il +7.0000jl +8.0000kl
+1.0000 +3.0000i +5.0000j +7.0000k +9.0000l +2.0000il +4.0000jl +6.0000kl
+8.0000 +7.0000i +6.0000j +5.0000k +4.0000l +3.0000il +2.0000jl +1.0000kl
Addition
a + b
output
+2.0000 +5.0000i +8.0000j +11.0000k +14.0000l +8.0000il +11.0000jl +14.0000kl
Subtraction
a - b
output
+0.0000 -1.0000i -2.0000j -3.0000k -4.0000l +4.0000il +3.0000jl +2.0000kl
Multiplication
a * b
output
-181.0000 -48.0000i -17.0000j -40.0000k +83.0000l +0.0000il +35.0000jl +4.0000kl
Division
a / b
output
+0.8281 +0.2353i +0.1041j +0.2172k -0.3303l +0.0543il -0.0950jl +0.0543kl
Norm
a.norm
output
14.2828568570857
Conjugation
a.conjugate
output
+1.0000 -2.0000i -3.0000j -4.0000k -5.0000l -6.0000il -7.0000jl -8.0000kl
Inverse
a.inverse
output
+0.0049 -0.0098i -0.0147j -0.0196k -0.0245l -0.0294il -0.0343jl -0.0392kl
Power
a ** 3
output
-608.0000 -400.0000i -600.0000j -800.0000k -1000.0000l -1200.0000il -1400.0000jl -1600.0000kl
Real Part
a.x_0
output
1
Similary, we can obtain coeficient of imaginary units
Example 1:
a.x_1
output
2
Example 2:
a.x_7
output
8
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file pyoctonion-3.12.tar.gz.
File metadata
- Download URL: pyoctonion-3.12.tar.gz
- Upload date:
- Size: 5.6 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.9.13
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a0ed5c58dc0f19368cc794eb076403b48a7cc6e35cf0a8bfe1e45f7d6b906d0c
|
|
| MD5 |
fdaba23a8739c842d176cde6a301e3fe
|
|
| BLAKE2b-256 |
05d60834fe6d98815415f57558f2432607b0f5ba73ab41f1eaffaaf00a5ada96
|
File details
Details for the file pyoctonion-3.12-py3-none-any.whl.
File metadata
- Download URL: pyoctonion-3.12-py3-none-any.whl
- Upload date:
- Size: 5.7 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.9.13
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
f9d29737235aa22a9c0b6e9bab2edca345f3f1259d528bd8ee89a6b7170107ef
|
|
| MD5 |
61c37df068a34b1fcf417fffe88dc727
|
|
| BLAKE2b-256 |
0aa602974d90fc4ee7af6c6b1f11d30541b5740b0596f7c9cda67515482b59a3
|