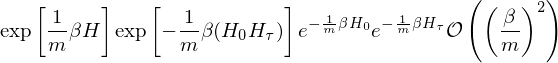pyqlearning is Python library to implement Reinforcement Learning and Deep Reinforcement Learning, especially for Q-Learning, Deep Q-Network, and Multi-agent Deep Q-Network which can be optimized by Annealing models such as Simulated Annealing, Adaptive Simulated Annealing, and Quantum Monte Carlo Method.
Project description
Reinforcement Learning Library: pyqlearning
pyqlearning is Python library to implement Reinforcement Learning and Deep Reinforcement Learning, especially for Q-Learning, Deep Q-Network, and Multi-agent Deep Q-Network which can be optimized by Annealing models such as Simulated Annealing, Adaptive Simulated Annealing, and Quantum Monte Carlo Method.
This library makes it possible to design the information search algorithm such as the Game AI, web crawlers, or Robotics. But this library provides components for designers, not for end-users of state-of-the-art black boxes. Briefly speaking the philosophy of this library, give user hype-driven blackboxes and you feed him for a day; show him how to design algorithms and you feed him for a lifetime. So algorithm is power.
|
Deep Reinforcement Learning (Deep Q-Network: DQN) to solve Maze. |
Multi-agent Deep Reinforcement Learning to solve the pursuit-evasion game. |
Installation
Install using pip:
pip install pyqlearning
Source code
The source code is currently hosted on GitHub.
Python package index(PyPI)
Installers for the latest released version are available at the Python package index.
Dependencies
Option
- accel-brain-base: v1.0.0 or higher.
- Only if you want to implement the Deep Reinforcement Learning.
- mxnet or mxnet-cu*: latest.
- Only when building a model of this library using Apache MXNet.
- torch
- Only when building a model of this library using PyTorch.
Documentation
Full documentation is available on https://code.accel-brain.com/Reinforcement-Learning/ . This document contains information on functionally reusability, functional scalability and functional extensibility.
Description
pyqlearning is Python library to implement Reinforcement Learning and Deep Reinforcement Learning, especially for Q-Learning, Deep Q-Network, and Multi-agent Deep Q-Network which can be optimized by Annealing models such as Simulated Annealing, Adaptive Simulated Annealing, and Quantum Monte Carlo Method.
This library provides components for designers, not for end-users of state-of-the-art black boxes. Reinforcement learning algorithms are highly variable because they must design single or multi-agent behavior depending on their problem setup. Designers of algorithms and architectures are required to design according to the situation at each occasion. Commonization and commoditization for end users who want easy-to-use tools is not easy. Nonetheless, commonality / variability analysis and object-oriented analysis are not impossible. I am convinced that a designer who can practice abstraction of concepts by drawing a distinction of concepts related to his/her own concrete problem settings makes it possible to distinguish commonality and variability of various Reinforcement Learning algorithms.
The commonality/variability of Epsilon Greedy Q-Leanring and Boltzmann Q-Learning
According to the Reinforcement Learning problem settings, Q-Learning is a kind of Temporal Difference learning(TD Learning) that can be considered as hybrid of Monte Carlo method and Dynamic Programming method. As Monte Carlo method, TD Learning algorithm can learn by experience without model of environment. And this learning algorithm is functional extension of bootstrap method as Dynamic Programming Method.
In this library, Q-Learning can be distinguished into Epsilon Greedy Q-Leanring and Boltzmann Q-Learning. These algorithm is functionally equivalent but their structures should be conceptually distinguished.
Epsilon Greedy Q-Leanring algorithm is a typical off-policy algorithm. In this paradigm, stochastic searching and deterministic searching can coexist by hyperparameter 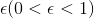
Boltzmann Q-Learning algorithm is based on Boltzmann action selection mechanism, where the probability
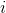
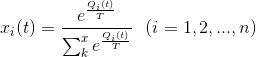
where the temperature 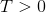
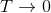
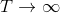
Commonality/variability of Q-learning models
Considering many variable parts and functional extensions in the Q-learning paradigm from perspective of commonality/variability analysis in order to practice object-oriented design, this library provides abstract class that defines the skeleton of a Q-Learning algorithm in an operation, deferring some steps in concrete variant algorithms such as Epsilon Greedy Q-Leanring and Boltzmann Q-Learning to client subclasses. The abstract class in this library lets subclasses redefine certain steps of a Q-Learning algorithm without changing the algorithm's structure.
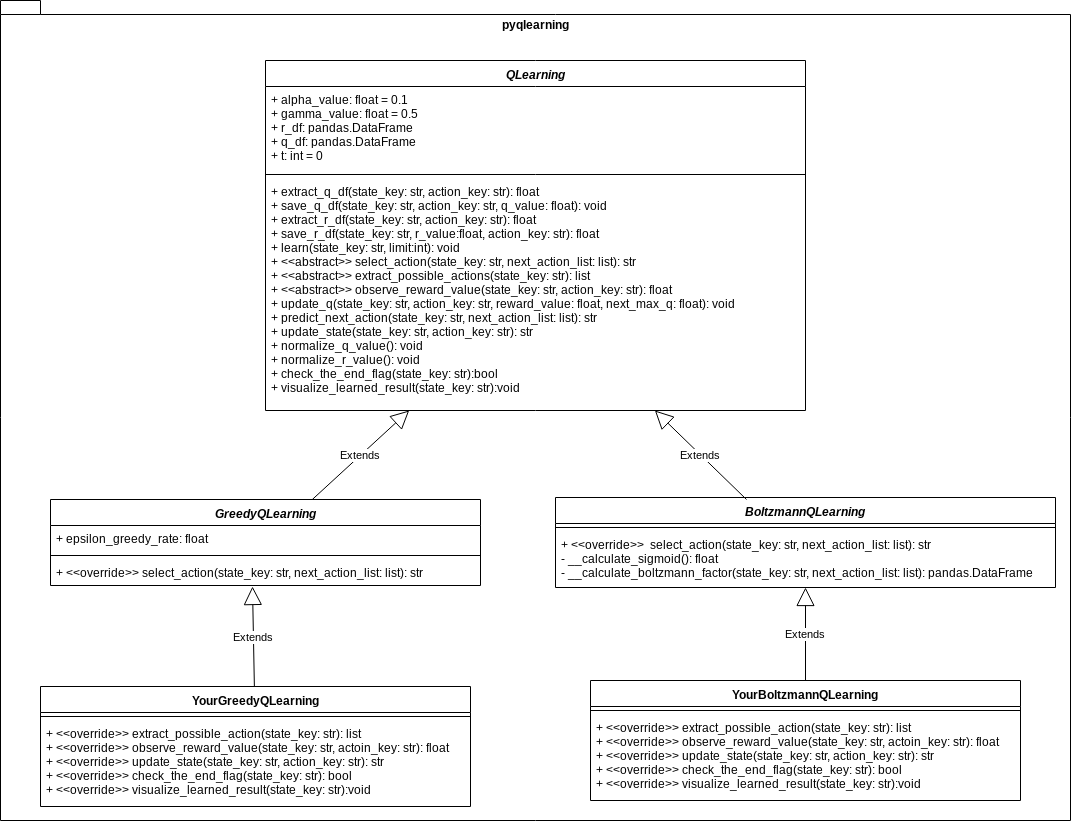
Typical concepts such as State, Action, Reward, and Q-Value in Q-learning models should be refered as viewpoints for distinguishing between commonality and variability. Among the functions related to these concepts, the class QLearning is responsible for more common attributes and behaviors. On the other hand, in relation to your concrete problem settings, more variable elements have to be implemented by subclasses such as YourGreedyQLearning or YourBoltzmannQLearning.
For more detailed specification of this template method, refer to API documentation: pyqlearning.q_learning module. If you want to know the samples of implemented code, see demo/.
Structural extension: Deep Reinforcement Learning
The Reinforcement learning theory presents several issues from a perspective of deep learning theory(Mnih, V., et al. 2013). Firstly, deep learning applications have required large amounts of hand-labelled training data. Reinforcement learning algorithms, on the other hand, must be able to learn from a scalar reward signal that is frequently sparse, noisy and delayed.
The difference between the two theories is not only the type of data but also the timing to be observed. The delay between taking actions and receiving rewards, which can be thousands of timesteps long, seems particularly daunting when compared to the direct association between inputs and targets found in supervised learning.
Another issue is that deep learning algorithms assume the data samples to be independent, while in reinforcement learning one typically encounters sequences of highly correlated states. Furthermore, in Reinforcement learning, the data distribution changes as the algorithm learns new behaviours, presenting aspects of recursive learning, which can be problematic for deep learning methods that assume a fixed underlying distribution.
Generalisation, or a function approximation
This library considers problem setteing in which an agent interacts with an environment 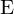
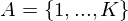
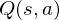
The goal of the agent is to interact with the 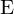
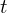
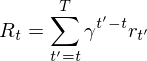
where 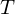
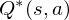

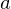
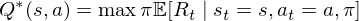
where 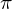
The optimal state/action-value function obeys an important identity known as the Bellman equation. This is based on the following intuition: if the optimal value 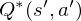
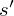
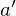
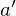
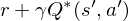
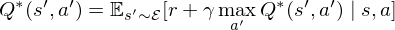
The basic idea behind many reinforcement learning algorithms is to estimate the state/action-value function, by using the Bellman equation as an iterative update,
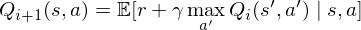
Such value iteration algorithms converge to the optimal state/action-value function, 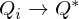
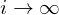
But increasing the complexity of states/actions is equivalent to increasing the number of combinations of states/actions. If the value function is continuous and granularities of states/actions are extremely fine, the combinatorial explosion will be encountered. In other words, this basic approach is totally impractical, because the state/action-value function is estimated separately for each sequence, without any generalisation. Instead, it is common to use a function approximator to estimate the state/action-value function,
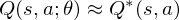
So the Reduction of complexities is required.
Deep Q-Network
In this problem setting, the function of nerual network or deep learning is a function approximation with weights 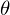
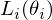
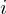
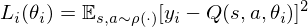
where
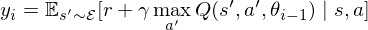
is the target for iteration 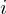
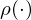
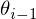
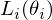
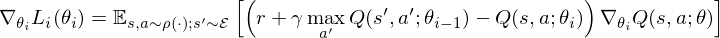
Tutorial: Maze Solving and the pursuit-evasion game by Deep Q-Network (Jupyter notebook)
demo/search_maze_by_deep_q_network.ipynb is a Jupyter notebook which demonstrates a maze solving algorithm based on Deep Q-Network, rigidly coupled with Deep Convolutional Neural Networks(Deep CNNs). The function of the Deep Learning is generalisation and CNNs is-a function approximator. In this notebook, several functional equivalents such as CNN and LSTM can be compared from a functional point of view.
- Black squares represent a wall.
- Light gray squares represent passages.
- A dark gray square represents a start point.
- A white squeare represents a goal point.
The pursuit-evasion game
Expanding the search problem of the maze makes it possible to describe the pursuit-evasion game that is a family of problems in mathematics and computer science in which one group attempts to track down members of another group in an environment.
This problem can be re-described as the multi-agent control problem, which involves decomposing the global system state into an image like representation with information encoded in separate channels. This reformulation allows us to use convolutional neural networks to efficiently extract important features from the image-like state.
Egorov, M. (2016) and Gupta, J. K. et al.(2017) proposed new algorithm which uses the image-like state representation of the multi-agent system as an input, and outputs the estimated Q-values for the agent in question. They described a number of implementation contributions that make training efficient and allow agents to learn directly from the behavior of other agents in the system.
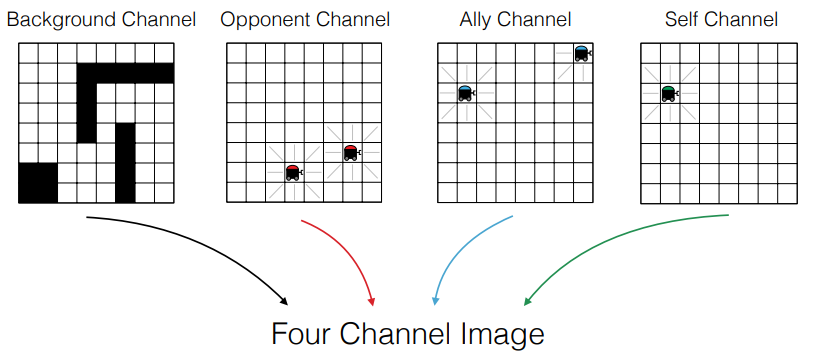
Egorov, M. (2016). Multi-agent deep reinforcement learning., p4.
An important aspect of this data modeling is that by expressing each state of the multi-agent as channels, it is possible to enclose states of all the agents as a target of convolution operation all at once. By the affine transformation executed by the neural network, combinations of an enormous number of states of multi-agent can be computed in principle with an allowable range of memory.
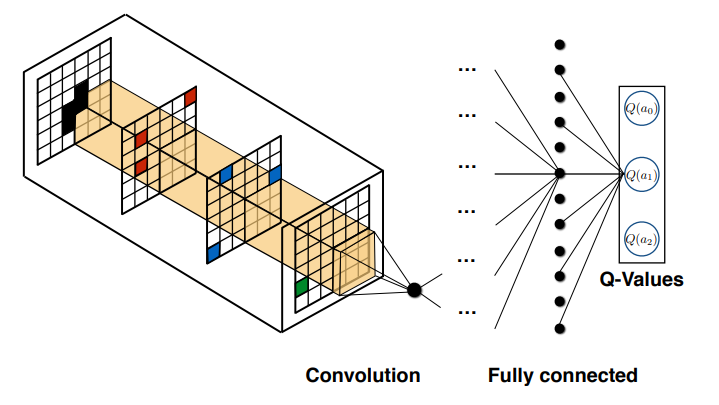
Egorov, M. (2016). Multi-agent deep reinforcement learning., p4.
demo/multi_agent_maze_by_deep_q_network.ipynb also prototypes Multi Agent Deep Q-Network to solve the pursuit-evasion game based on the image-like state representation of the multi-agent.
|
Multi-agent Deep Reinforcement Learning to solve the pursuit-evasion game. The player is caught by enemies. |
Multi-agent Deep Reinforcement Learning to solve the pursuit-evasion game. The player reaches the goal. |
- Black squares represent a wall.
- Light gray squares represent passages.
- A dark gray square represents a start point.
- Moving dark gray squares represent enemies.
- A white squeare represents a goal point.
Tutorial: Complexity of Hyperparameters, or how can be hyperparameters decided?
There are many hyperparameters that we have to set before the actual searching and learning process begins. Each parameter should be decided in relation to Deep/Reinforcement Learning theory and it cause side effects in training model. Because of this complexity of hyperparameters, so-called the hyperparameter tuning must become a burden of Data scientists and R & D engineers from the perspective of not only a theoretical point of view but also implementation level.
Combinatorial optimization problem and Simulated Annealing.
This issue can be considered as Combinatorial optimization problem which is an optimization problem, where an optimal solution has to be identified from a finite set of solutions. The solutions are normally discrete or can be converted into discrete. This is an important topic studied in operations research such as software engineering, artificial intelligence(AI), and machine learning. For instance, travelling sales man problem is one of the popular combinatorial optimization problem.
In this problem setting, this library provides an Annealing Model to search optimal combination of hyperparameters. For instance, Simulated Annealing is a probabilistic single solution based search method inspired by the annealing process in metallurgy. Annealing is a physical process referred to as tempering certain alloys of metal, glass, or crystal by heating above its melting point, holding its temperature, and then cooling it very slowly until it solidifies into a perfect crystalline structure. The simulation of this process is known as simulated annealing.
Functional comparison.
demo/annealing_hand_written_digits.ipynb is a Jupyter notebook which demonstrates a very simple classification problem: Recognizing hand-written digits, in which the aim is to assign each input vector to one of a finite number of discrete categories, to learn observed data points from already labeled data how to predict the class of unlabeled data. In the usecase of hand-written digits dataset, the task is to predict, given an image, which digit it represents.
There are many structural extensions and functional equivalents of Simulated Annealing. For instance, Adaptive Simulated Annealing, also known as the very fast simulated reannealing, is a very efficient version of simulated annealing. And Quantum Monte Carlo, which is generally known a stochastic method to solve the Schrödinger equation, is one of the earliest types of solution in order to simulate the Quantum Annealing in classical computer. In summary, one of the function of this algorithm is to solve the ground state search problem which is known as logically equivalent to combinatorial optimization problem. Then this Jupyter notebook demonstrates functional comparison in the same problem setting.
Demonstration: Epsilon Greedy Q-Learning and Simulated Annealing.
Import python modules.
from pyqlearning.annealingmodel.costfunctionable.greedy_q_learning_cost import GreedyQLearningCost
from pyqlearning.annealingmodel.simulated_annealing import SimulatedAnnealing
# See demo/demo_maze_greedy_q_learning.py
from demo.demo_maze_greedy_q_learning import MazeGreedyQLearning
The class GreedyQLearningCost is implemented the interface CostFunctionable to be called by AnnealingModel. This cost function is defined by
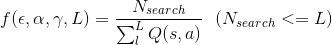
where 
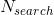
Like Monte Carlo method, let us draw random samples from a normal (Gaussian) or unifrom distribution.
# Epsilon-Greedy rate in Epsilon-Greedy-Q-Learning.
greedy_rate_arr = np.random.normal(loc=0.5, scale=0.1, size=100)
# Alpha value in Q-Learning.
alpha_value_arr = np.random.normal(loc=0.5, scale=0.1, size=100)
# Gamma value in Q-Learning.
gamma_value_arr = np.random.normal(loc=0.5, scale=0.1, size=100)
# Limit of the number of Learning(searching).
limit_arr = np.random.normal(loc=10, scale=1, size=100)
var_arr = np.c_[greedy_rate_arr, alpha_value_arr, gamma_value_arr, limit_arr]
Instantiate and initialize MazeGreedyQLearning which is-a GreedyQLearning.
# Instantiation.
greedy_q_learning = MazeGreedyQLearning()
greedy_q_learning.initialize(hoge=fuga)
Instantiate GreedyQLearningCost which is implemented the interface CostFunctionable to be called by AnnealingModel.
init_state_key = ("Some", "data")
cost_functionable = GreedyQLearningCost(
greedy_q_learning,
init_state_key=init_state_key
)
Instantiate SimulatedAnnealing which is-a AnnealingModel.
annealing_model = SimulatedAnnealing(
# is-a `CostFunctionable`.
cost_functionable=cost_functionable,
# The number of annealing cycles.
cycles_num=5,
# The number of trials of searching per a cycle.
trials_per_cycle=3
)
Fit the var_arr to annealing_model.
annealing_model.var_arr = var_arr
Start annealing.
annealing_model.annealing()
To extract result of searching, call the property predicted_log_list which is list of tuple: (Cost, Delta energy, Mean of delta energy, probability in Boltzmann distribution, accept flag). And refer the property x which is np.ndarray that has combination of hyperparameters. The optimal combination can be extracted as follow.
# Extract list: [(Cost, Delta energy, Mean of delta energy, probability, accept)]
predicted_log_arr = annealing_model.predicted_log_arr
# [greedy rate, Alpha value, Gamma value, Limit of the number of searching.]
min_e_v_arr = annealing_model.var_arr[np.argmin(predicted_log_arr[:, 2])]
Contingency of definitions
The above definition of cost function is possible option: not necessity but contingent from the point of view of modal logic. You should questions the necessity of definition and re-define, for designing the implementation of interface CostFunctionable, in relation to your problem settings.
Demonstration: Epsilon Greedy Q-Learning and Adaptive Simulated Annealing.
There are various Simulated Annealing such as Boltzmann Annealing, Adaptive Simulated Annealing(SAS), and Quantum Simulated Annealing. On the premise of Combinatorial optimization problem, these annealing methods can be considered as functionally equivalent. The Commonality/Variability in these methods are able to keep responsibility of objects all straight as the class diagram below indicates.
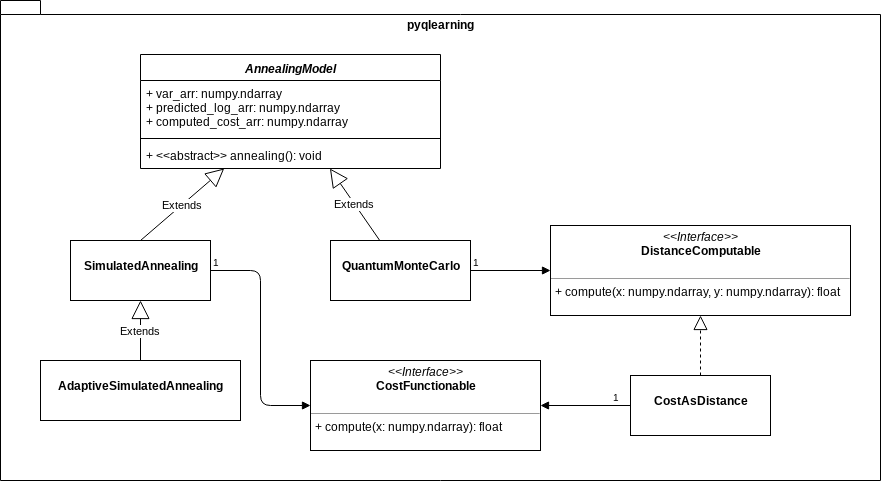
Code sample.
AdaptiveSimulatedAnnealing is-a subclass of SimulatedAnnealing. The variability is aggregated in the method AdaptiveSimulatedAnnealing.adaptive_set() which must be called before executing AdaptiveSimulatedAnnealing.annealing().
from pyqlearning.annealingmodel.simulatedannealing.adaptive_simulated_annealing import AdaptiveSimulatedAnnealing
annealing_model = AdaptiveSimulatedAnnealing(
cost_functionable=cost_functionable,
cycles_num=33,
trials_per_cycle=3,
accepted_sol_num=0.0,
init_prob=0.7,
final_prob=0.001,
start_pos=0,
move_range=3
)
# Variability part.
annealing_model.adaptive_set(
# How often will this model reanneals there per cycles.
reannealing_per=50,
# Thermostat.
thermostat=0.,
# The minimum temperature.
t_min=0.001,
# The default temperature.
t_default=1.0
)
annealing_model.var_arr = params_arr
annealing_model.annealing()
To extract result of searching, call the property like the case of using SimulatedAnnealing. If you want to know how to visualize the searching process, see my Jupyter notebook: demo/annealing_hand_written_digits.ipynb.
Demonstration: Epsilon Greedy Q-Learning and Quantum Monte Carlo.
Generally, Quantum Monte Carlo is a stochastic method to solve the Schrödinger equation. This algorithm is one of the earliest types of solution in order to simulate the Quantum Annealing in classical computer. In summary, one of the function of this algorithm is to solve the ground state search problem which is known as logically equivalent to combinatorial optimization problem.
According to theory of spin glasses, the ground state search problem can be described as minimization energy determined by the hamiltonian 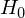
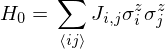
where 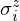
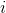
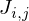
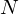
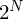
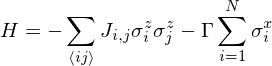
where 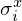
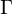
In relation to this system, thermal equilibrium amount of a physical quantity 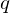
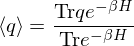
If 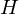
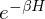
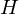
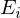
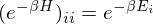
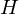
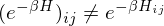
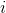
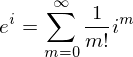
Therefore, a path integration based on Trotter-Suzuki decomposition has been introduced in Quantum Monte Carlo Method. This path integration makes it possible to obtain the partition function 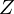
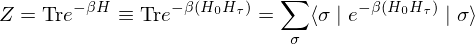
where if 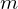
Then the partition function 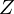
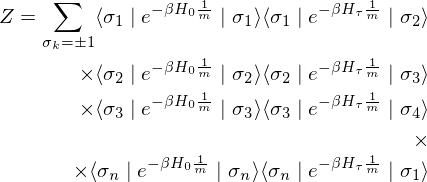
where 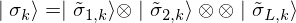
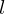
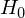
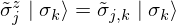
Therefore,
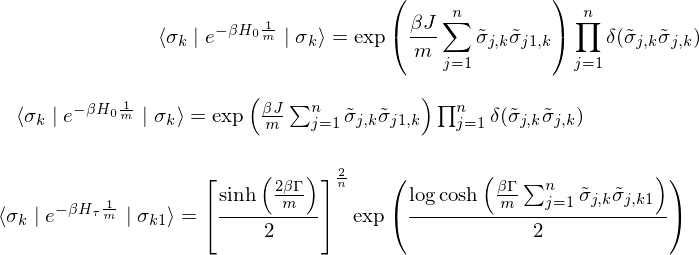
The partition function 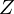
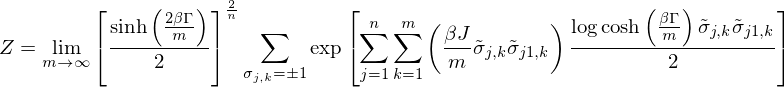
where 
This relational expression indicates that the quantum - mechanical Hamiltonian in 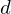

Code sample.
from pyqlearning.annealingmodel.quantum_monte_carlo import QuantumMonteCarlo
from pyqlearning.annealingmodel.distancecomputable.cost_as_distance import CostAsDistance
# User defined function which is-a `CostFuntionable`.
cost_functionable = YourCostFunctions()
# Compute cost as distance for `QuantumMonteCarlo`.
distance_computable = CostAsDistance(params_arr, cost_functionable)
# Init.
annealing_model = QuantumMonteCarlo(
distance_computable=distance_computable,
# The number of annealing cycles.
cycles_num=100,
# Inverse temperature (Beta).
inverse_temperature_beta=0.1,
# Gamma. (so-called annealing coefficient.)
gammma=1.0,
# Attenuation rate for simulated time.
fractional_reduction=0.99,
# The dimention of Trotter.
trotter_dimention=10,
# The number of Monte Carlo steps.
mc_step=100,
# The number of parameters which can be optimized.
point_num=100,
# Default `np.ndarray` of 2-D spin glass in Ising model.
spin_arr=None,
# Tolerance for the optimization.
# When the ΔE is not improving by at least `tolerance_diff_e`
# for two consecutive iterations, annealing will stops.
tolerance_diff_e=0.01
)
# Execute annealing.
annealing_model.annealing()
To extract result of searching, call the property like the case of using SimulatedAnnealing. If you want to know how to visualize the searching process, see my Jupyter notebook: demo/annealing_hand_written_digits.ipynb.
References
The basic concepts, theories, and methods behind this library are described in the following books.

『「AIの民主化」時代の企業内研究開発: 深層学習の「実学」としての機能分析』(Japanese)

『AI vs. ノイズトレーダーとしての投資家たち: 「アルゴリズム戦争」時代の証券投資戦略』(Japanese)

『自然言語処理のバベル: 文書自動要約、文章生成AI、チャットボットの意味論』(Japanese)

『統計的機械学習の根源: 熱力学、量子力学、統計力学における天才物理学者たちの神学的な理念』(Japanese)
Specific references are the following papers and books.
Q-Learning models.
- Agrawal, S., & Goyal, N. (2011). Analysis of Thompson sampling for the multi-armed bandit problem. arXiv preprint arXiv:1111.1797.
- Bubeck, S., & Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems. arXiv preprint arXiv:1204.5721.
- Chapelle, O., & Li, L. (2011). An empirical evaluation of thompson sampling. In Advances in neural information processing systems (pp. 2249-2257).
- Du, K. L., & Swamy, M. N. S. (2016). Search and optimization by metaheuristics (p. 434). New York City: Springer.
- Kaufmann, E., Cappe, O., & Garivier, A. (2012). On Bayesian upper confidence bounds for bandit problems. In International Conference on Artificial Intelligence and Statistics (pp. 592-600).
- Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
- Richard Sutton and Andrew Barto (1998). Reinforcement Learning. MIT Press.
- Watkins, C. J. C. H. (1989). Learning from delayed rewards (Doctoral dissertation, University of Cambridge).
- Watkins, C. J., & Dayan, P. (1992). Q-learning. Machine learning, 8(3-4), 279-292.
- White, J. (2012). Bandit algorithms for website optimization. ” O’Reilly Media, Inc.”.
Deep Q-Network models.
- Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
- Egorov, M. (2016). Multi-agent deep reinforcement learning.
- Gupta, J. K., Egorov, M., & Kochenderfer, M. (2017, May). Cooperative multi-agent control using deep reinforcement learning. In International Conference on Autonomous Agents and Multiagent Systems (pp. 66-83). Springer, Cham.
- Malhotra, P., Ramakrishnan, A., Anand, G., Vig, L., Agarwal, P., & Shroff, G. (2016). LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv preprint arXiv:1607.00148.
- Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
- Sainath, T. N., Vinyals, O., Senior, A., & Sak, H. (2015, April). Convolutional, long short-term memory, fully connected deep neural networks. In Acoustics, Speech and Signal Processing (ICASSP), 2015 IEEE International Conference on (pp. 4580-4584). IEEE.
- Xingjian, S. H. I., Chen, Z., Wang, H., Yeung, D. Y., Wong, W. K., & Woo, W. C. (2015). Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Advances in neural information processing systems (pp. 802-810).
- Zaremba, W., Sutskever, I., & Vinyals, O. (2014). Recurrent neural network regularization. arXiv preprint arXiv:1409.2329.
Annealing models.
- Bektas, T. (2006). The multiple traveling salesman problem: an overview of formulations and solution procedures. Omega, 34(3), 209-219.
- Bertsimas, D., & Tsitsiklis, J. (1993). Simulated annealing. Statistical science, 8(1), 10-15.
- Das, A., & Chakrabarti, B. K. (Eds.). (2005). Quantum annealing and related optimization methods (Vol. 679). Springer Science & Business Media.
- Du, K. L., & Swamy, M. N. S. (2016). Search and optimization by metaheuristics. New York City: Springer.
- Edwards, S. F., & Anderson, P. W. (1975). Theory of spin glasses. Journal of Physics F: Metal Physics, 5(5), 965.
- Facchi, P., & Pascazio, S. (2008). Quantum Zeno dynamics: mathematical and physical aspects. Journal of Physics A: Mathematical and Theoretical, 41(49), 493001.
- Heim, B., Rønnow, T. F., Isakov, S. V., & Troyer, M. (2015). Quantum versus classical annealing of Ising spin glasses. Science, 348(6231), 215-217.
- Heisenberg, W. (1925) Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 33, pp.879—893.
- Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift fur Physik, 43, 172-198.
- Heisenberg, W. (1984). The development of quantum mechanics. In Scientific Review Papers, Talks, and Books -Wissenschaftliche Übersichtsartikel, Vorträge und Bücher (pp. 226-237). Springer Berlin Heidelberg. Hilgevoord, Jan and Uffink, Jos, "The Uncertainty Principle", The Stanford Encyclopedia of Philosophy (Winter 2016 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2016/entries/qt-uncertainty/>.
- Jarzynski, C. (1997). Nonequilibrium equality for free energy differences. Physical Review Letters, 78(14), 2690.
- Messiah, A. (1966). Quantum mechanics. 2 (1966). North-Holland Publishing Company.
- Mezard, M., & Montanari, A. (2009). Information, physics, and computation. Oxford University Press.
- Nallusamy, R., Duraiswamy, K., Dhanalaksmi, R., & Parthiban, P. (2009). Optimization of non-linear multiple traveling salesman problem using k-means clustering, shrink wrap algorithm and meta-heuristics. International Journal of Nonlinear Science, 8(4), 480-487.
- Schrödinger, E. (1926). Quantisierung als eigenwertproblem. Annalen der physik, 385(13), S.437-490.
- Somma, R. D., Batista, C. D., & Ortiz, G. (2007). Quantum approach to classical statistical mechanics. Physical review letters, 99(3), 030603.
- 鈴木正. (2008). 「組み合わせ最適化問題と量子アニーリング: 量子断熱発展の理論と性能評価」.,『物性研究』, 90(4): pp598-676. 参照箇所はpp619-624.
- 西森秀稔、大関真之(2018) 『量子アニーリングの基礎』須藤 彰三、岡 真 監修、共立出版、参照箇所はpp9-46.
Author
- accel-brain
Author URI
License
- GNU General Public License v2.0
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file pyqlearning-1.2.7.tar.gz.
File metadata
- Download URL: pyqlearning-1.2.7.tar.gz
- Upload date:
- Size: 59.1 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.9.17
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
996a2444b9c121bccd4cf2681eb73fd2080a33355d7d85b1de039e3886bd0a13
|
|
| MD5 |
9b4313205e33129bd9bb99a2d5fcbdfd
|
|
| BLAKE2b-256 |
cd6b0f819a8ea4395fe6d5a00cf05d0465d12f786e04f23bd6f74537ee7c3b18
|