pyviewfactor 0.0.16

A python library to calculate numerically exact radiation view factors between planar faces.

PyViewFactor

A python library to compute exact view factors between planar faces (Documentation).

This code computes the radiation view factor between polygons using the double contour integral method described in (Mazumder and Ravishankar 2012) and (Schmid 2016).

It uses the handy Pyvista package to deal with geometrical aspects of such problems.

How does it work?

• Use pyvista to import your geometry (*.stl, *.vtk, *.obj, ...) or alternately draw it with the same package.
• Optionally check that the faces can "see" each other with get_visibility(face1, face2)
• Optionally check that no obstruction lies between them get_visibility_obstruction(face1, face2, obstacle)
• Compute the view factor from face2 to face1 with compute_view_factor(face1, face2): Done!

Minimum working example : facet to facet view factor computation

Suppose we want to compute the radiation view factor between a triangle and a rectangle.

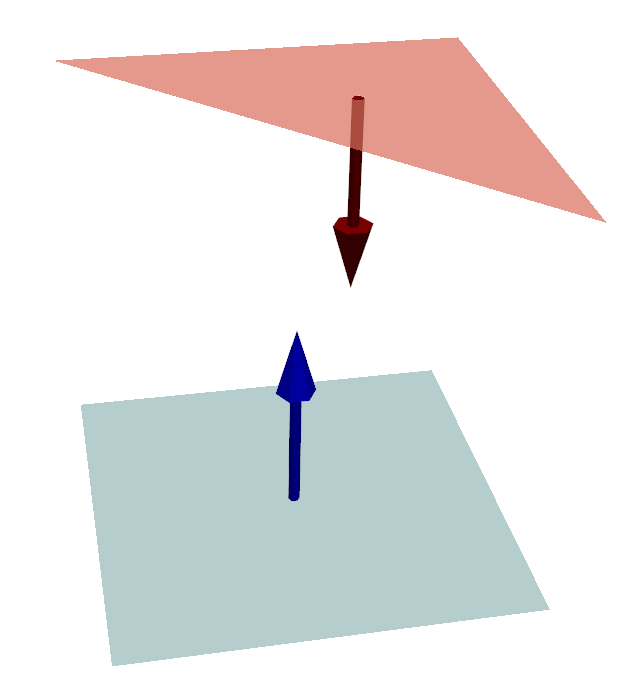
You are now 18 lines of code away from your first view factor computation:

import pyvista as pv
import pyviewfactor as pvf

# first define a rectangle...
pointa = [1, 0, 0] 
pointb = [1, 1, 0]
pointc = [0, 1, 0]
pointd = [0, 0, 0]
rectangle = pv.Rectangle([pointa, pointb, pointc, pointd])

# ... then a triangle
pointa = [1, 0, 1] 
pointb = [1, 1, 1]
pointc = [0, 1, 1]
liste_pts = [pointa, pointb, pointc]
liste_pts.reverse() # let us put the normal the other way around (facing the rectangle)
triangle = pv.Triangle(liste_pts) # ... done with geometry.

# preliminary check for visibility
if pvf.get_visibility(rectangle , triangle):
    F = pvf.compute_viewfactor(rectangle, triangle)
    print("View factor from triangle to rectangle = ", F)
else:
    print("Not facing each other")

You usually get your geometry from a different format? (*.idf, *.dat, ...)

Check pyvista's documentation on how to generate a PolyData facet from points.

Example with a closed geometry and the VTK file format

We will now compute the view factors within a more complex geometry: a closed sphere (clipped in half below), with inwards facing normals, so the faces can "see" each other. Note that the face-to-face visibility is unobstructed (for obstructed geometries, see next section).

The field of view factors from one facet to all others will be computed and stored in a VTK file, which you can explore with the open source Paraview software.

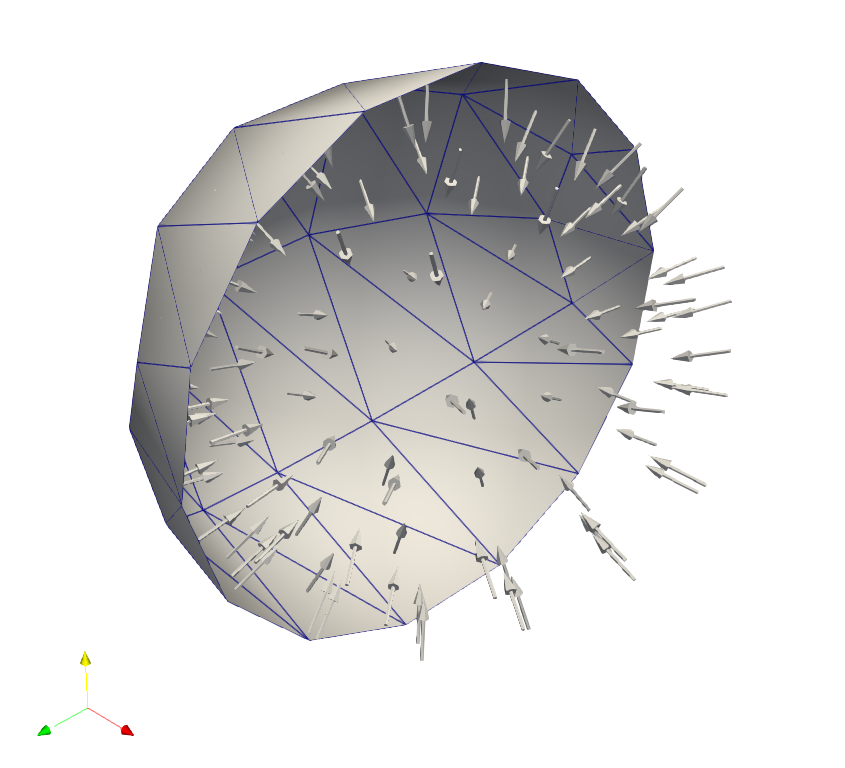
Following snippet can be reused as a kick-start for your own purposes:

import pyvista as pv
import numpy as np
from pyviewfactor import  compute_viewfactor, fc_unstruc2poly # viewfactor + a useful conversion function
from tqdm import tqdm # for a fancy progress bar

# create a raw sphere with pyvista
sphere = pv.Sphere(radius=50, center=(0, 0, 0), direction=(0, 0, 1),
                 theta_resolution=9, phi_resolution=9)
# and put the normals inwards please
sphere.flip_normals()

# let us chose a cell to compute view factors from
chosen_face = sphere.extract_cells(10)
# convert the face from UnstructuredGrid to PolyData
chosen_face = fc_unstruc2poly(chosen_face)
# "one array to contain them all" -> the results will be stored there
F = np.zeros(sphere.n_cells) 

# now let us compute the view factor to all other faces
# (with a fancy progress bar, iterating over the mesh's faces)
for i in tqdm(range(sphere.n_cells), total=sphere.n_cells):
    face = sphere.extract_cells(i) # other facet
    face = fc_unstruc2poly(face) # convert to PolyData
    F[i] = compute_viewfactor(face, chosen_face) # compute VF

print("Complementarity check: \n (e.g. is \sum_{i=0}^n F_i =? 1)", np.sum(F))

# put the scalar values in the geometry
sphere.cell_data["F"] = F
sphere.save("./sphere.vtk") # ... and save.

# let us have a look in 3D with an interactive window...
p=pv.Plotter() # instantiate 3D window
p.add_mesh(sphere, scalars='F', cmap='jet') # add mesh with a nice color scheme
p.show() # plot

The results look as per following images showing the view factor from the chosen cell to all others.

View factors of an individual with a wall

For comfort computations, it may be useful to determine heat transfer between an invidivual and a wall. We will use here PyVista's doorman example as a basis for the human geometry.

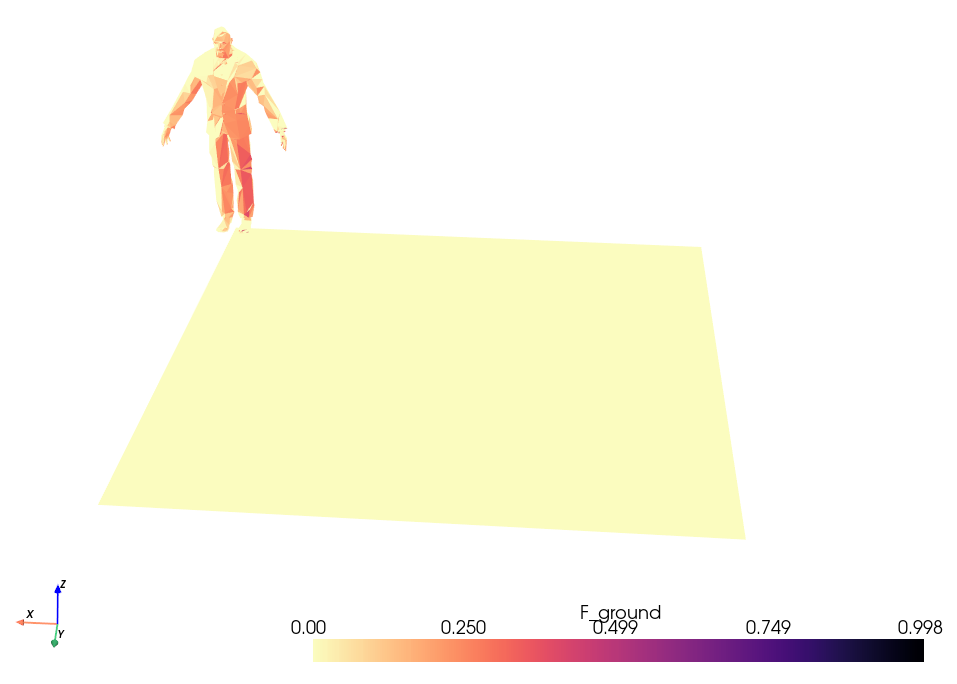
The following code and VTK file of the doorman example are available in the ./examples/ folder.

# -*- coding: utf-8 -*-
from tqdm import tqdm
import numpy as np
import pyvista as pv
import pyviewfactor as pvf

def fc_Fwall(nom_vtk):
    mesh=pv.read(nom_vtk)
    
    # find all types of walls
    wall_types=list(np.unique(mesh['names']))
    # remove the individual from the list (still named 'cylinder'...)
    wall_types.remove('cylinder\r') # with dirty trailing character
    # where is the doorman in the list?
    index_doorman=np.where(mesh['names']=='cylinder\r')[0]
    # prepare storage for the different walls in a dict
    dict_F={}
    # loop over wall types
    for type_wall in wall_types:
        # prepare for storing doorman to wall view factor
        F=np.zeros(mesh.n_cells)
        # get the indices of this type of wall
        indices=np.where(mesh['names']==type_wall )[0]
        # loop over
        for i in indices:
            wall=mesh.extract_cells(i)
            wall=pvf.fc_unstruc2poly(wall) # convert for normals
            # ... for each facet of the individual
            for idx in tqdm(index_doorman):
                face = mesh.extract_cells(idx)
                face =pvf.fc_unstruc2poly(face) # convert for normals
                # check if faces can "see" each other
                if pvf.get_visibility(wall,face):
                    Ffp=pvf.compute_viewfactor(wall,face) # compute face2wall view factor
                else:
                    Ffp=0
                F[idx]=Ffp
        #store array F in e.g. dict_F['F_ceiling']
        dict_F['F_'+type_wall.replace('\r','')]=F
    return dict_F

# download it directly from https://gitlab.com/arep-dev/pyViewFactor/-/blob/main/examples/example_doorman.vtk ...
# ...or get it from this repository's examples
file="./example_doorman.vtk"
# compute the view factors or the doorman to the different wall types in the scene
dict_F=fc_Fwall(file)

# re-read and store
mesh=pv.read(file)
# loop over what is in the dictionary of view factors
for elt in dict_F.keys():
    mesh[elt.replace('\r','')]=dict_F[elt] # name the field
mesh.save(file) # store in the intial VTK

# have a look without paraview with fancy colors
mesh.plot(cmap='jet',lighting=False)

More details and view abacuses in this page. Is the computation time a bit lengthy? Learn how to go parallel!.

Computing the view factors of a wall in its built environment

For building simulation purposes, it may prove to be useful to compute the ground and sky view factors of a given wall, or the view factor of the wall to other walls in the built environment. In following example (available in the "examples" folder), we compute the view factors of the environment of the purple wall depicted below.

import numpy as np
import pyvista as pv
from tqdm import tqdm
import pyviewfactor as pvf

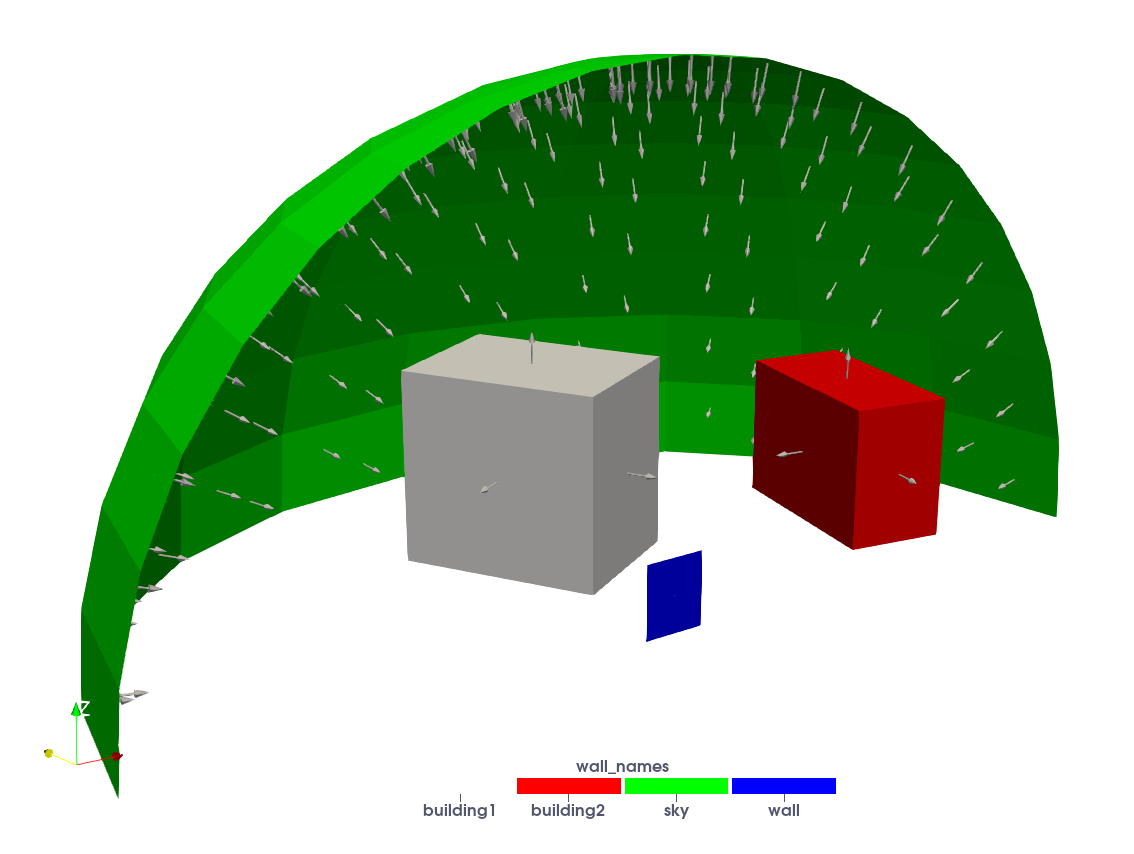
# read the geometry
mesh = pv.read("./built_envmt.vtk")
meshpoly = pvf.fc_unstruc2poly(mesh) # convert to polydata for obstruction check

# identify who is who
i_wall = np.where(mesh["wall_names"]=='wall')[0]
i_sky = np.where(mesh["wall_names"]=='sky')[0]
i_building1 = np.where(mesh["wall_names"]=='building1')[0]
i_building2 = np.where(mesh["wall_names"]=='building2')[0]

# get the different elements
wall = mesh.extract_cells(i_wall)
sky = mesh.extract_cells(i_sky)
building1 = mesh.extract_cells(i_building1)
building2 = mesh.extract_cells(i_building2)

# convert to polydata
wall = pvf.fc_unstruc2poly(wall)

Fsky = 0
# for all cells constituting the ensemble
for patch in tqdm(i_sky):
    sky = mesh.extract_cells(patch) # extract one cell
    sky = pvf.fc_unstruc2poly(sky) # convert to polydata
    if pvf.get_visibility(sky, wall): # if the can see each other...
        if pvf.get_visibility_raytrace(sky, wall, meshpoly): # ... if no obstruction
            Fsky += pvf.compute_viewfactor(sky, wall) # compute and increment view factor : F_i->(j+k) = F_i->j + F_i->k

# same for building 1
Fbuilding1 = 0
for patch in tqdm(i_building1):
    bldng1 = mesh.extract_cells(patch)
    bldng1 = pvf.fc_unstruc2poly(bldng1)
    if pvf.get_visibility(bldng1, wall):
        if pvf.get_visibility_raytrace(bldng1, wall, meshpoly):
            Fbuilding1 += pvf.compute_viewfactor(bldng1, wall)

# same for building 2
Fbuilding2 = 0
for patch in tqdm(i_building2):
    bldng2 = mesh.extract_cells(patch)
    bldng2 = pvf.fc_unstruc2poly(bldng2)
    if pvf.get_visibility(bldng2, wall):
        if pvf.get_visibility_raytrace(bldng2, wall, meshpoly):
            Fbuilding2 += pvf.compute_viewfactor(bldng2, wall)

# complementarity implies \sigma F_i = 1 : compute viewfactor to ground
Fground = 1-Fbuilding1-Fbuilding2-Fsky

print('\n----------------------')
print('Wall to environment view factors :')
print('\tSky ', round(Fsky, 4))
print('\tBuilding 1 ', round(Fbuilding1, 4))
print('\tBuilding 2 ', round(Fbuilding2, 4))
print('Ground view factor :')
print('\tGround ', round(Fground, 4))

The code yields following view factors :

F_{\text{sky}} = 0.345 \\
F_{\text{ground}} = 0.373 \\
F_{\text{building1}} = 0.251 \\
F_{\text{building2}} = 0.031 \\

Understanding the obstruction check function

In real life problems, obstacles may well hinder the radiation heat transfer between surfaces. We make use here of pyvista's raytrace function to perform obstruction tests, as per following example, much inspired from pyvista's online documentation.

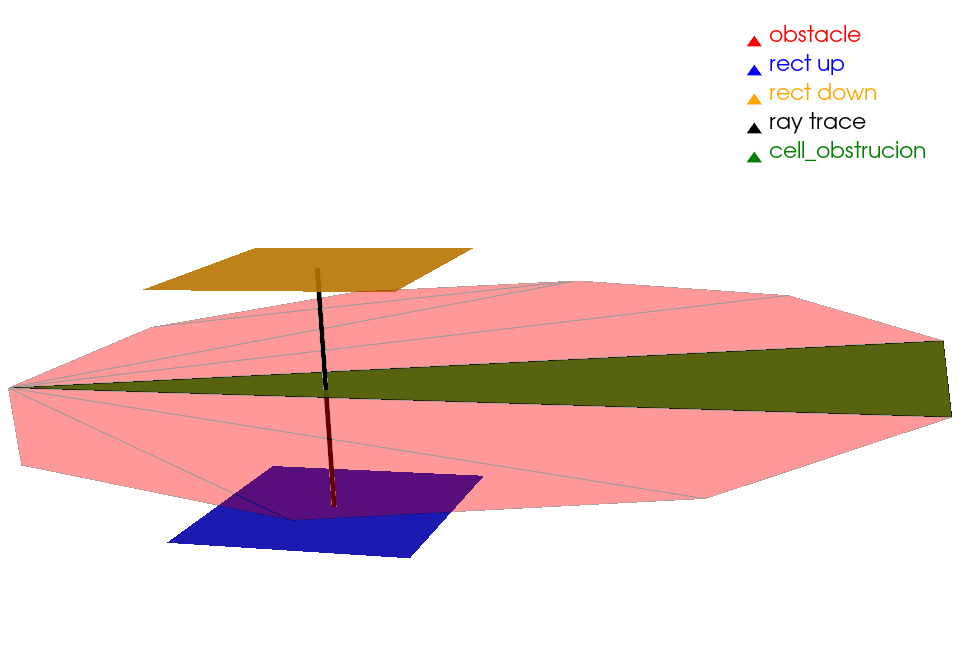
The code snippet below shows how the ray tracing function works and allows to understand its usage in the pyviewfactor get_visibility_raytrace function.

import pyvista as pv
from pyviewfactor import get_visibility_raytrace
# let us first create two rectangles
pointa = [1, 0, 0]
pointb = [1, 1, 0]
pointc = [0, 1, 0]
pointd = [0, 0, 0]
rectangle_down = pv.Rectangle([pointa, pointb, pointc, pointd])
pointa = [1, 0, 1]
pointb = [1, 1, 1]
pointc = [0, 1, 1]
pointd = [0, 0, 1]
rectangle_up = pv.Rectangle([pointa, pointb, pointc, pointd])

# a circle will be the obstruction
z_translation, r = 0.5, 2
obstacle = pv.Circle(radius=r, resolution=10)
# we translate the obstruction right between both rectangles
obstacle.translate([0, 0, z_translation], inplace=True)
# Define line segment
start = rectangle_down.cell_centers().points[0]
stop = rectangle_up.cell_centers().points[0]
# Perform ray trace
points, ind = obstacle.ray_trace(start, stop)

# Create geometry to represent ray trace
ray = pv.Line(start, stop)
intersection = pv.PolyData(points)

# Render the result
p = pv.Plotter(notebook=True)
p.add_mesh(obstacle, show_edges=True, opacity=0.5, color="red", lighting=False, label="obstacle")
p.add_mesh(rectangle_up, color="blue", line_width=5, opacity=0.5, label="rect up")
p.add_mesh(rectangle_down, color="yellow", line_width=5,opacity=0.5, label="rect down")
p.add_mesh(ray, color="green", line_width=5, label="ray trace")

# if any intersection
if intersection.n_cells > 0:
    p.add_mesh(intersection, color="green", point_size=25, label="Intersection Points")
p.add_legend()
p.show(cpos="yz")

#now a call to the obstruction check function
print(get_visibility_raytrace(rectangle_up, rectangle_down, obstacle))

More complex scenes can then be treated with the function get_visibility_raytrace.

Installation

pyViewFactor can be installed from PyPi using pip on Python >= 3.7:

pip install pyviewfactor

You can also visit PyPi or Gitlab to download the sources.

Requirements:

numpy==1.17.4
pandas==1.4.2
pyvista==0.35.2
scipy==1.8.1
numba>=0.55.2

The code will probably work with lower versions of the required packages, however this has not been tested.

Note - If you are alergic to numba, you may pip install pyviewfactor==0.0.10 that works (and give up the x2 speed-up in view factor computation).

Authors and acknowledgment

Mateusz BOGDAN, Edouard WALTHER, Marc ALECIAN, Mina CHAPON

Citation

There is even a conference paper, showing analytical validations :

Mateusz BOGDAN, Edouard WALTHER, Marc ALECIAN and Mina CHAPON. Calcul des facteurs de forme entre polygones - Application à la thermique urbaine et aux études de confort. IBPSA France 2022, Châlons-en-Champagne.

Bibtex entry:

@inproceedings{pyViewFactor22bogdan,
  authors      = "Mateusz BOGDAN and Edouard WALTHER and Marc ALECIAN and Mina CHAPON",
  title        = "Calcul des facteurs de forme entre polygones - Application à la thermique urbaine et aux études de confort",
  year         = "2022",
  organization = "IBPSA France",
  venue        = "Châlons-en-Champagne, France"
  note         = "IBPSA France 2022",
}

License

MIT License - Copyright (c) AREP 2022