Quantitative Financial Risk Management: awesome OOP tools for measuring, managing and visualizing risk of financial instruments and portfolios.
Project description
Quantitative Financial Risk Management (QFRM) project is a (rapidly growing) set of analytical tools to measure, manage and visualize identified risks of derivatives and portfolios in finance.
Why use Quantitative Financial Risk Management (QFRM) package:
We apply object-oriented programming (OOP) paradigm to abstract the complexities of financial valuation.
Plentiful examples: each class has a numerous examples, including sensitivity plots and multidimensional visualization.
Resources: we included references (J.C.Hull’s OFOD textbook, academic research and online resources) we used to build and validate our analytical tools.
Simplicity, consistency and usability: QFRM uses basic data structures as user inputs inputs/outputs (I/O).
Longevity: qfrm dependencies are limited to Python Standard Library, pandas, numpy, scipy, and matplotlib.
We try to sensibly vectorize our functions to help you with application of QFRM functionality.
All programing is done with usability/scalability/extendability/performance in mind.
This project grows rapidly with an effort from a dozen of bright quant finance developers. Check back for updates throughout Fall 2015.
Our Team:
This is a group of ambitious and diligent Rice University science students from doctoral, masters and undergraduate programs. United in their work, we expand and contribute to finance community and QFRM course, led by Oleg Melnikov, a statistics doctoral student and instructor of QFRM course at Rice University, Department of Statistics.
Oleg Melnikov (author, creator), Department of Statistics, Rice University, http://Oleg.Rice.edu, xisreal@gmail.com
Thaw Da Aung (contributor), Department of Physics, Thawda.Aung@rice.edu
Yen-Fei Chen (contributor), Department of Statistics, Yen-Fei.Chen@rice.edu
Patrick J. Granahan (contributor), Department of Computer Science, pjgranahan@rice.edu
Hanting Li (contributor), Department of Statistics, HANTING.LI@rice.edu
Sha (Andy) Liao (contributor), Department of Physics, Andy.Liao@rice.edu
Scott Morgan (contributor), Department of Computer Science, spmorgan@rice.edu
Andrew M. Weatherly (contributor), Department of Computational and Applied Mathematics, amw13@rice.edu
Mengyan Xie (contributor), Department of Electrical Engineering, Mengyan.Xie@rice.edu
Tianyi Yao (contributor), Department of Electrical Engineering, Tianyi.Yao@rice.edu
Runmin Zhang (contributor), Department of Physics, Runmin.Zhang@rice.edu
OOP Design and functionality:
In progress:
Bond pricing is temporarily disabled (will return soon), but you’ll find numerous exotic option pricing (via Black-Scholes model, lattice tree, Monte Carlo simulation and finite differencing) in the package.
- class PVCF (present value of cash flows) accepts time-indexed cash flows and a yield curve to compute:
net present value (NPV), internal rate or return (IRR), time value of money (TVM)
Linearly interpolated yield curve with time-to-maturities (TTM) matching those of cash flows (CF)
Visualization: CF diagram
- class Bond (inherits PVCF) accepts coupon/frequency/TTM specification along with optional yield curve (with optional TTM) to compute:
- Valuation and performance analytics: clean/dirty price, yield to maturity (ytm), par and current yield
interest rates (IR) are assumed to be continuously compounded (CC), but user has a method to convert from/to any frequency.
Risk analytics: Macaulay/Modified/Effective durations, convexity
Visualization: CF diagram, dirty/clean price convergence, price sensitivity curves and slopes with and without convexity adjustment.
class Util provides some helpful functionality for verifying/standardizing in I/O of other class’ methods.
Planned implementation:
Fixed income portfolio analytics, exotic option pricing (via lattice, Black-Scholes model (BSM), Monte Carlo simulations, and Finite Differencing Methods (FDM)), and further visualization of concepts in finance.
Genesis:
This project started as a QFRM R package in Spring 2015 QFRM course (STAT 449 and STAT 649) at Rice University.
The course is part of computational finance and economic systems (CoFES) program, led by Dr. Katherine Ensor.
Underlying textbook (source of financial calculations and algorithms)
Options, Futures and other Derivatives (OFOD) by John C. Hull, 9ed, 2014, ISBN 0133456315 is a well established text in finance and risk management. Major certification exams in finance (CFA, FRM, CAIA, CQF, …) list it as a core reference.
Install:
Directly from PyPI with pip command in a terminal (or windows command, cmd.exe) prompt, assuming pip is in your PATH:
$ pip install qfrmTypical usage:
3% annually-paying bond with 3.1 TTM (in years), evaluated at 5% continuously compounded (CC) yield-to-maturity (YTM), i.e. flat yield curve (YC)
>>> Bond(3,1,3.1, pyz=.05).analytics()
------------------ Bond analytics: ------------------------
* Annual coupon, $: 3
* Coupon frequency, p.a.: 1
Time to maturity (ttm), yrs: 3.1
* Cash flows, $ p.a.: (3.0, 3.0, 3.0, 103.0)
Time to cash flows (ttcf), yrs: (0.10000000000000009, 1.1, 2.1, 3.1)
Dirty price (PVCF), $: 96.73623
* Clean price (PVCF - AI), $: 94.03623
YTM, CC rate: 0.05
YTM, rate at coupon frequency: 0.05127
Current yield, rate at coupon frequency: 0.0319
* Par yield, rate at coupon frequency: 0.03883
Yield curve, CC rate: (0.05, 0.05, 0.05, 0.05)
Macaulay duration, yrs: 2.9208
Modified duration, yrs: 2.77835
Effective duration, yrs: 2.92126
* Convexity, yrs^2: 8.92202
Desc: {}
------------------------------------------------------------------------------
Median run time (microsec) for 1 iteration(s): 11604.918843659107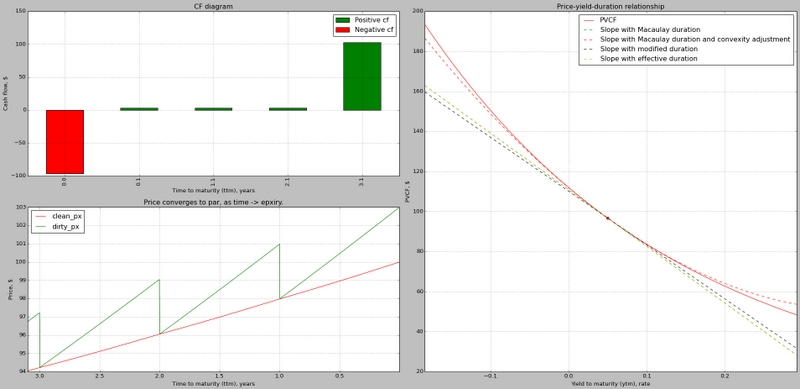
Textbook example (default) of 6% SA bond with 2 years/time to maturity (TTM), see p.83 in Hull’s OFOD/9ed
>>> Bond().analytics()4% semi-annual (SA) bond with 4.25 ttm (4 years and 3 mo), evaluated at $97.5 PVCF (which computes to 4.86% ytm or flat YC)
>>> b = Bond(4,2,4.25, pyz=97.5)
>>> b.ytm() # compute yield from supplied (PVCF) price ($97.5 assumed)
0.048615328294339864
>>> b.ytm(px_target=(97.5, 98, 99, 100, 101)) # vectorized computation of yield-to-maturity
(0.048615328294339864, 0.047305618596811434, 0.04470725938701976, 0.04213648737177501, 0.039592727021145635)
>>> b.analytics() # prints full report and visualizationThe same 4% SA bond evaluated with a specific YC. Zero rates are assumed to have TTM matching those of cash flows (CF), left to right. Insufficient rates are extrapolated with a constant.
>>> b.set_pyz(pyz=(.05,.06,.07,.08)).analytics()The same 4% SA bond evaluated with a specific YC. User provides zero rates with corresponding TTM. TTM required to evaluate CF are extra/interpolated from existing curve with constant rates on each side.
>>> b.set_pyz(pyz=(.05,.06,.04,.03), ttz=(.5,1,2,6)).analytics()This project uses industry-accepted acronyms:
AI: accrued interest
APT: arbitrage pricing theorem
ASP: active server pages (i.e. HTML scripting on server side) by Microsoft
b/w: between
bip: basis points
BM: Brownian motion (aka Wiener Process)
Bmk: benchmark
BOPM: binomial option pricing model
bp: basis points
BSM: Black-Scholes model or Black-Scholes-Merton model
BT: binomial tree
c.c.: continuous compounding
CC: continuous compounding
CCP: central counterparty
CCRR: continuously compounded rate of return
CDS: credit default swap
CDO: credit default obligation
CF: cash flows
Cmdt: commodity
Corp: corporate (finance or sector)
CP: counterparty (in finance)
CUSIP: Committee on Uniform Security Identification Procedures, North-American financial security identifier (like ISIN)
ESO: employee stock option
ETD: exchange-traded derivative
FE: financial engineering
FDM: Finite differencing method
FRA: forward rate agreement
FRN: floating rate notes
Fwd: forward
FX: foreign currency or foreign currency exchange
FV: future value
GBM: geometric Brownian motion
Gvt: government
Hld: holding
Idx: index
IM: initial margin
IR: interest rate
IRD: interest rate derivatives
IRTS: interest rate term structure
ISIN: International Securities Identification Number
LIBID: London Interbank bid rate
LIBOR: London Interbank Offered Rate
LT: lattice tree (i.e binomial, trinomial, …)
MA: margin account; moving average
MC: margin call
MC: Monte Carlo simulation
Mgt: management
Mkt: market
MM: maintenance margin
MP: Markov process
MTM: marking to market
Mtge: mortgage
MV: multivariate
OFOD: Options, Futures, and Other Derivatives
OFOD9e: Options, Futures, and Other Derivatives, 9th edition
OIS: overnight index SWAP rate
OOP: object oriented programming
p.a.: per annum
PD: probability of default
PDE: partial differential equation
PM: portfolio manager
PORTIA: portfolio accounting system by Thomson Financial
Pts: points
PV: present value
PVCF: present value of cash flows
QFRM: quantitative financial risk management
REPO: Repurchase agreement rate
RFR: risk free rate
RN: risk-neutral
RNW: risk-neutral world
RoI: return on investment
RoR: rate of return
r.v.: random variable
s.a.: semi-annual
SA: semi-annual
SAC: semi-annual compounding
SP: stochastic process
SQL: sequel query language
SQP: standard Wiener process
SURF: step up recovery floaters (floating rate notes)
TBA: to be announced
TBD: To be determined
TOMS: Trade Order Management Solution (or System)
Trx: transaction
TS: time series
TSA: time series analysis
TTCF: time to cash flows
TTM: time to maturity
TVM: time value of money
UDF: user defined function
URL: universe resource locator
VaR: value at risk
Var: variance
VB: Visual Basic (by Microsoft)
VBA: Visual Basic for Applications
Vol: volatility
WAC: weighted-average coupon
WAM: weighted-average maturity
WP: Wiener process (aka Brownian motion)
YC: yield curve
Yld: yield
ZCB: zero coupon bond
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file qfrm-0.2.0.27.zip.
File metadata
- Download URL: qfrm-0.2.0.27.zip
- Upload date:
- Size: 116.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
1a43e83c2cd2d8c3e86662aae559f859ea3e9c4ec637bd4e62bb7a304533aa02
|
|
| MD5 |
644c4b55d0c4f593fd331364877f8691
|
|
| BLAKE2b-256 |
a1a9ccc342903a8375b9686405d4443c94f20b25a68c27d633d9285f391a5f56
|
File details
Details for the file qfrm-0.2.0.27-py3-none-any.whl.
File metadata
- Download URL: qfrm-0.2.0.27-py3-none-any.whl
- Upload date:
- Size: 110.7 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
eefacfbd5dce7d68dffa040da328eaf84e0b76457b7fc2962ccf3feca56b2f96
|
|
| MD5 |
653d74e485830ebe8d406e06c2fe216f
|
|
| BLAKE2b-256 |
ea7ffb0e34cc75d3129f40dd3b0292e051851c320b064b3587d0a3d2df5179f4
|










