Benchmark for quadratic programming solvers available in Python.
Project description
QP solvers benchmark
Benchmark for quadratic programming (QP) solvers available in Python.
The goal of this benchmark is to help users compare and select QP solvers. Its methodology is open to discussions. The benchmark ships standard and community test sets, as well as a qpsolvers_benchmark command-line tool to run test sets directly. The main output of the benchmark are standardized reports evaluating all metrics across all QP solvers available on the test machine. This repository also distributes results from running the benchmark on a reference computer.
New test sets are welcome! The benchmark is designed so that each test-set comes in a standalone directory. Feel free to create a new one and contribute it here so that we grow the collection over time.
Test sets
The benchmark comes with standard and community test sets to represent different use cases for QP solvers:
| Test set | Problems | Brief description |
|---|---|---|
| Maros-Meszaros | 138 | Standard, designed to be difficult. |
| Maros-Meszaros dense | 62 | Subset of Maros-Meszaros restricted to smaller dense problems. |
| GitHub free-for-all | 12 | Community-built, new problems are welcome! |
Solvers
| Solver | Keyword | Algorithm | Matrices | License |
|---|---|---|---|---|
| Clarabel | clarabel |
Interior point | Sparse | Apache-2.0 |
| CVXOPT | cvxopt |
Interior point | Dense | GPL-3.0 |
| DAQP | daqp |
Active set | Dense | MIT |
| ECOS | ecos |
Interior point | Sparse | GPL-3.0 |
| Gurobi | gurobi |
Interior point | Sparse | Commercial |
| HiGHS | highs |
Active set | Sparse | MIT |
| HPIPM | hpipm |
Interior point | Dense | BSD-2-Clause |
| MOSEK | mosek |
Interior point | Sparse | Commercial |
| NPPro | nppro |
Active set | Dense | Commercial |
| OSQP | osqp |
Douglas–Rachford | Sparse | Apache-2.0 |
| ProxQP | proxqp |
Augmented Lagrangian | Dense & Sparse | BSD-2-Clause |
| qpOASES | qpoases |
Active set | Dense | LGPL-2.1 |
| qpSWIFT | qpswift |
Interior point | Sparse | GPL-3.0 |
| quadprog | quadprog |
Goldfarb-Idnani | Dense | GPL-2.0 |
| SCS | scs |
Douglas–Rachford | Sparse | MIT |
Metrics
We evaluate QP solvers based on the following metrics:
- Success rate: percentage of problems a solver is able to solve on a given test set.
- Computation time: time a solver takes to solve a given problem.
- Optimality conditions: we evaluate all three optimality conditions:
- Primal residual: maximum error on equality and inequality constraints at the returned solution.
- Dual residual: maximum error on the dual feasibility condition at the returned solution.
- Duality gap: value of the duality gap at the returned solution.
- Cost error: difference between the solution cost and the known optimal cost.
Shifted geometric mean
Each metric (computation time, primal and dual residuals, duality gap) produces a different ranking of solvers for each problem. To aggregate those rankings into a single metric over the whole test set, we use the shifted geometric mean (shm), which is a standard to aggregate computation times in benchmarks for optimization software. This mean has the advantage of being compromised by neither large outliers (as opposed to the arithmetic mean) nor by small outliers (in contrast to the geometric geometric mean). Check out the references below for further details.
Here are some intuitive interpretations:
- A solver with a shifted-geometric-mean runtime of $Y$ is $Y$ times slower than the best solver over the test set.
- A solver with a shifted-geometric-mean primal residual $R$ is $R$ times less accurate on equality and inequality constraints than the best solver over the test set.
Results
The outcome from running a test set is a standardized report comparing solvers against the different metrics. Here are the results obtained on a reference computer:
| Test set | Results | CPU info |
|---|---|---|
| GitHub free-for-all | Full report | Intel(R) Core(TM) i7-6500U CPU @ 2.50GHz |
| Maros-Meszaros | Full report | Intel(R) Core(TM) i7-6500U CPU @ 2.50GHz |
| Maros-Meszaros dense | Full report | Intel(R) Core(TM) i7-6500U CPU @ 2.50GHz |
You can check out results from a variety of machines, and share the reports produced by running the benchmark on your own machine, in the Results category of the discussions forum.
Limitations
Here are some known areas of improvement for this benchmark:
- Cold start only: we don't evaluate warm-start performance for now.
Check out the issue tracker for ongoing works and future improvements.
Installation
You can install the benchmark and its dependencies in an isolated environment using conda:
conda create -f environment.yaml
conda activate qpsolvers_benchmark
Alternatively, you can install the benchmark on your system using pip:
pip install qpsolvers_benchmark
By default, the benchmark will run all supported solvers it finds.
Running the benchmark
Once the benchmark is installed, you will be able to run the qpsolvers_benchmark command. Provide it with the script corresponding to the test set you want to run, followed by a benchmark command such as "run". For instance, let's run the "dense" subset of the Maros-Meszaros test set:
qpsolvers_benchmark maros_meszaros/maros_meszaros_dense.py run
You can also run a specific solver, problem or set of solver settings:
qpsolvers_benchmark maros_meszaros/maros_meszaros_dense.py run --solver proxqp --settings default
Check out qpsolvers_benchmark --help for a list of available commands and arguments.
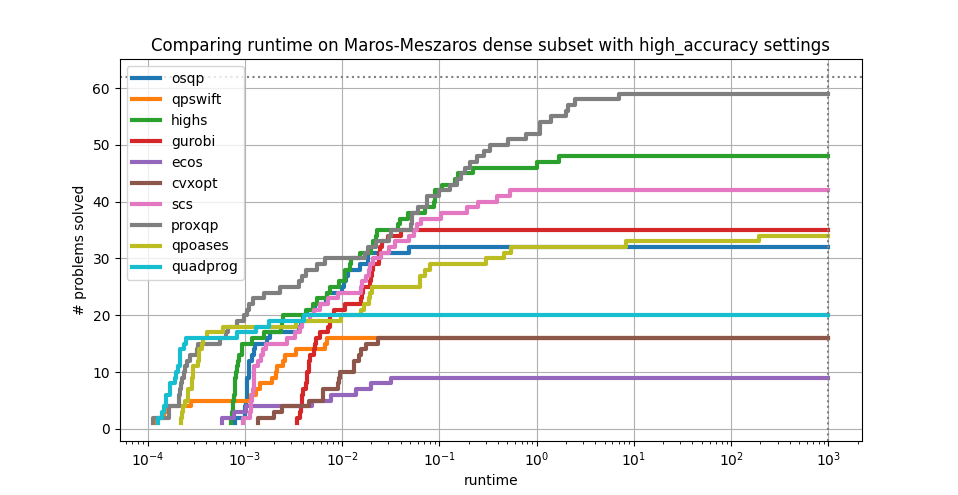
Plots
The command line ships a plot command to compare solver performances over a test set for a specific metric. For instance, run:
qpsolvers_benchmark maros_meszaros/maros_meszaros_dense.py plot runtime high_accuracy
To generate the following plot:
Contributing
Contributions to improving this benchmark are welcome. You can for instance propose new problems, or share the runtimes you obtain on your machine. Check out the contribution guidelines for details.
See also
References
- How not to lie with statistics: the correct way to summarize benchmark results: why geometric means should always be used to summarize normalized results.
- Optimality conditions and numerical tolerances in QP solvers: note written while figuring out the
high_accuracysettings of this benchmark.
Other benchmarks
- Benchmarks for optimization software by Hans Mittelmann, which includes reports on the Maros-Meszaros test set.
- jrl-qp/benchmarks: benchmark of QP solvers available in C++.
- osqp_benchmark: benchmark examples for the OSQP solver.
- proxqp_benchmark: benchmark examples for the ProxQP solver.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file qpsolvers_benchmark-1.1.0.tar.gz.
File metadata
- Download URL: qpsolvers_benchmark-1.1.0.tar.gz
- Upload date:
- Size: 32.3 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: python-requests/2.28.2
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 5532a05ae7e4070318988abc4eec64fa5c2ef87e0031d040dc1ed1c9b2f638c8 |
|
| MD5 | a27ab64ee30b28f849f0777f047dc178 |
|
| BLAKE2b-256 | 35cc1a59bcf0f8ebe85013a106aede7383cc1e559df93a870e5c333c076e961e |
File details
Details for the file qpsolvers_benchmark-1.1.0-py3-none-any.whl.
File metadata
- Download URL: qpsolvers_benchmark-1.1.0-py3-none-any.whl
- Upload date:
- Size: 38.1 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: python-requests/2.28.2
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ce0c718990ea75331d104afcae1e9d9256de8d9d36aa9d35c002a6f4c1fa52cc |
|
| MD5 | 639aa9cb4961455135093f6c3c7a158c |
|
| BLAKE2b-256 | b33663a119a88414472b215d534eadec7cbe60f9fcf9dacdf28a2d5fd825b1c8 |