Differentiable and accelerated spherical transforms with JAX
Project description
S2FFT is a Python package for computing Fourier transforms on the sphere
and rotation group (Price & McEwen 2024) using
JAX or PyTorch. It leverages autodiff to provide differentiable transforms, which are
also deployable on hardware accelerators (e.g. GPUs and TPUs).
More specifically, S2FFT provides support for spin spherical harmonic
and Wigner transforms (for both real and complex signals), with support
for adjoint transformations where needed, and comes with different
optimisations (precompute or not) that one may select depending on
available resources and desired angular resolution $L$.
Algorithms ⚡
S2FFT leverages new algorithmic structures that can he highly
parallelised and distributed, and so map very well onto the architecture
of hardware accelerators (i.e. GPUs and TPUs). In particular, these
algorithms are based on new Wigner-d recursions that are stable to high
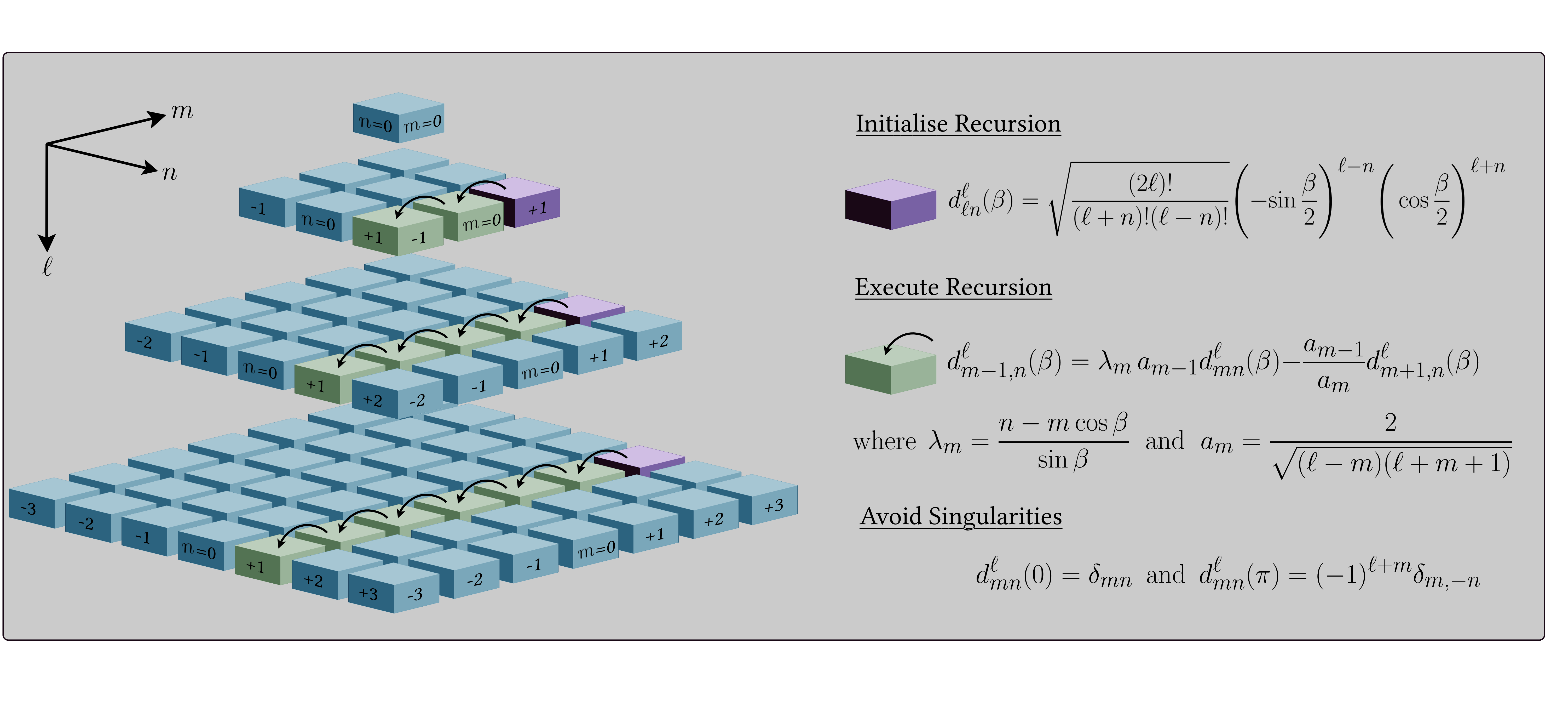
angular resolution $L$. The diagram below illustrates the recursions
(for further details see Price & McEwen 2024).
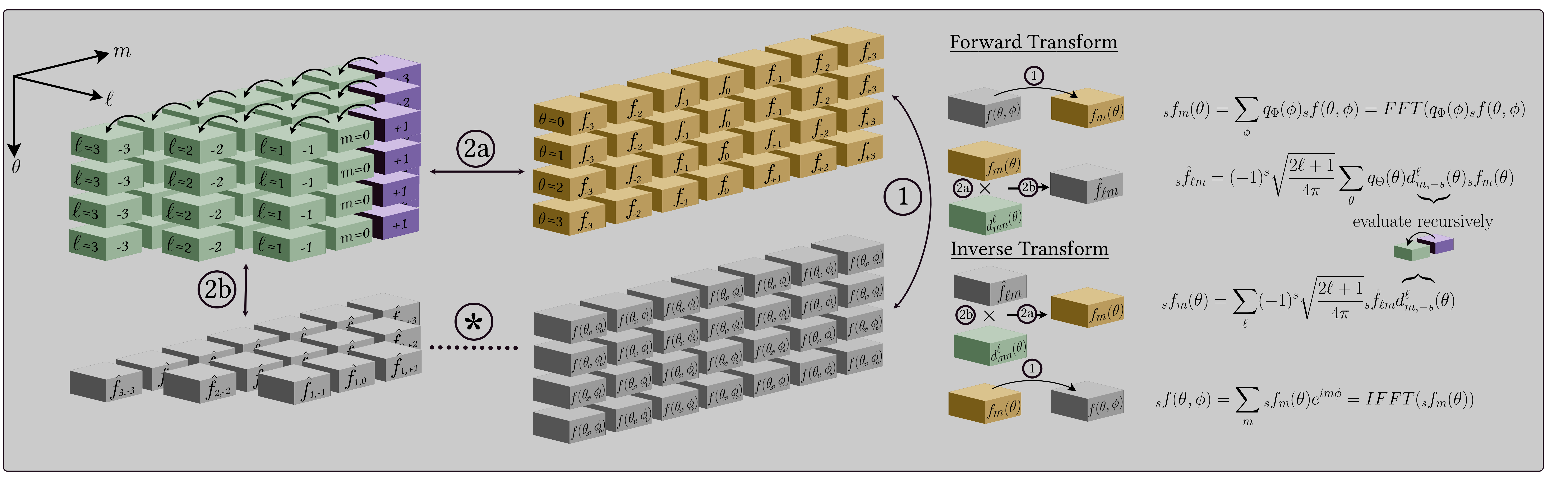
With this recursion to hand, the spherical harmonic coefficients of an isolatitudinally sampled map may be computed as a two step process. First, a 1D Fourier transform over longitude, for each latitudinal ring. Second, a projection onto the real polar-d functions. One may precompute and store all real polar-d functions for extreme acceleration, however this comes with an equally extreme memory overhead, which is infeasible at $L \sim 1024$. Alternatively, the real polar-d functions may calculated recursively, computing only a portion of the projection at a time, hence incurring negligible memory overhead at the cost of slightly slower execution. The diagram below illustrates the separable spherical harmonic transform (for further details see Price & McEwen 2024).
Sampling 🌍
The structure of the algorithms implemented in S2FFT can support any
isolatitude sampling scheme. A number of sampling schemes are currently
supported.
The equiangular sampling schemes of McEwen & Wiaux (2012), Driscoll & Healy (1995) and Gauss-Legendre (1986) are supported, which exhibit associated sampling theorems and so harmonic transforms can be computed to machine precision. Note that the McEwen & Wiaux sampling theorem reduces the Nyquist rate on the sphere by a factor of two compared to the Driscoll & Healy approach, halving the number of spherical samples required.
The popular HEALPix sampling scheme (Gorski et al. 2005) is also supported. The HEALPix sampling does not exhibit a sampling theorem and so the corresponding harmonic transforms do not achieve machine precision but exhibit some error. However, the HEALPix sampling provides pixels of equal areas, which has many practical advantages.
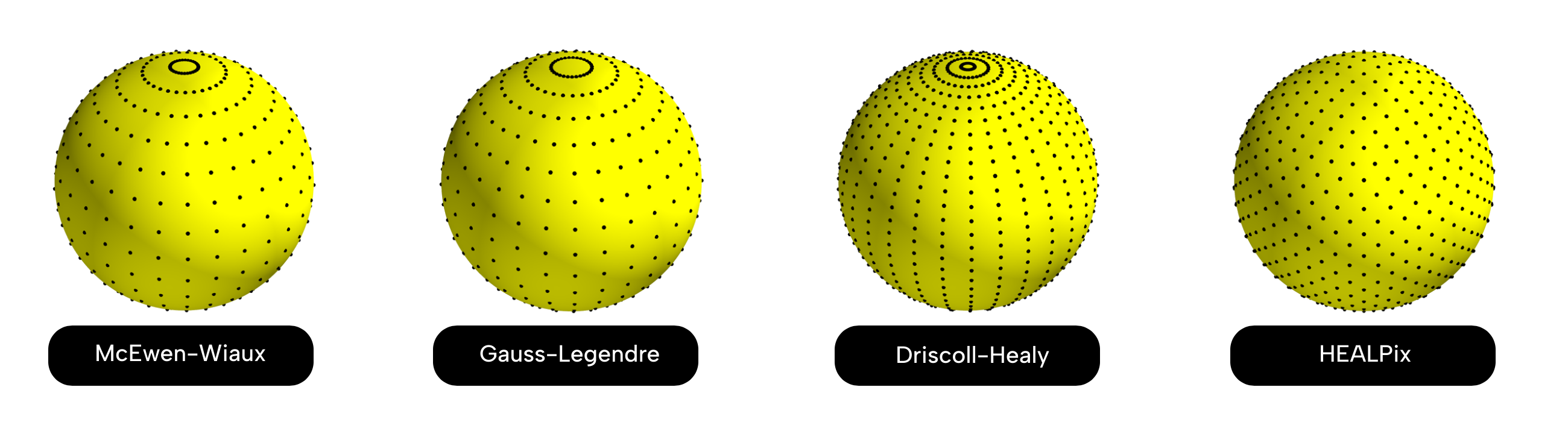
[!NOTE] For algorithmic reasons JIT compilation of HEALPix transforms can become slow at high bandlimits, due to XLA unfolding of loops. After compilation, HEALPix transforms should execute with the efficiency outlined in the associated paper, therefore this additional time overhead need only be incurred once.
If running on a CPU, we provide (differentiable) JAX wrappers of the
healpytransforms which can be used to sidestep the issue. This implementation can be selected by passing amethod="jax_healpy"keyword argument to thes2fft.forwardors2fft.inversefunctions - see example notebook.If running on a GPU, a CUDA extension module is available which avoids the long compilation time. This implementation can be selected by passing a
method="jax_cuda"keyword argument to thesfft.forwardands2fft.inversefunctions. Currently we do not publish binary wheels with the CUDA extension support so you will need to build the package from source to use this functionality.
Installation 💻
The latest release of S2FFT published on PyPI can be installed by running
pip install s2fft
This will install S2FFT's dependencies including JAX if not already installed.
As by default installing JAX from PyPI will use a CPU-only build,
if you wish to install JAX with GPU or TPU support,
you should first follow the relevant installation instructions in JAX's documentation
and then install S2FFT as above.
Alternatively, the latest development version of S2FFT may be installed directly from GitHub by running
pip install git+https://github.com/astro-informatics/s2fft
CUDA extension support
To install the package with support for the CUDA extension module giving reduced compile times for running HEALPix transforms on the GPU, you will need to build from source on a system with CUDA (tested with version 12.3) and CMake (versions 3.19+) installed.
To install the latest development version from source in verbose mode run
pip install -v git+https://github.com/astro-informatics/s2fft
or to install a specific release tag in verbose mode run
pip install -v git+https://github.com/astro-informatics/s2fft@TAG
where TAG is the relevant version tag.
The output should indicate if the CUDA install on your system is successfully detected.
Tests 🚦
A pytest test suite for the package is included in the tests directory.
To install the test dependencies, clone the repository and install the package (in editable mode)
with the extra test dependencies by running from the root of the repository
pip install -e ".[tests]"
To run the tests, run from the root of the repository
pytest
Documentation 📖
Documentation for the released version is available here. To install the documentation dependencies, clone the repository and install the package (in editable mode) with the extra documentation dependencies by running from the root of the repository
pip install -e ".[docs]"
To build the documentation, run from the root of the repository
cd docs
make html
open _build/html/index.html
Notebooks 📓
A series of tutorial notebooks are included in the notebooks directory
and rendered in the documentation.
To install the dependencies required to run the notebooks locally, clone the repository and install the package (in editable mode) with the extra documentation and plotting dependencies by running from the root of the repository
pip install -e ".[docs,plotting]"
To run the notebooks in Jupyter Lab, run from the root of the repository
jupyter lab
Usage 🚀
To import and use S2FFT is as simple follows:
For a signal on the sphere
import s2fft
# Define sampled signal to transform and harmonic bandlimit
f = ...
L = ...
# Compute harmonic coefficients
flm = s2fft.forward(f, L, method="jax")
# Map back to pixel-space signal
f = s2fft.inverse(flm, L, method="jax")
For a signal on the rotation group
import s2fft
# Define sampled signal to transform and harmonic and azimuthal bandlimits
f = ...
L = ...
N = ...
# Compute Wigner coefficients
flmn = s2fft.wigner.forward(f, L, N, method="jax")
# Map back to pixel-space signal
f = fft.wigner.inverse_jax(flmn, L, N, method="jax")
For further details on usage see the documentation and associated notebooks.
We also provide PyTorch support for our transforms, as demonstrated in the Torch frontend tutorial notebook. This wraps the JAX implementations so JAX will need to be installed in addition to PyTorch.
SSHT & HEALPix wrappers 💡
S2FFT also provides JAX support for existing C/C++ packages, specifically HEALPix and SSHT. This works
by wrapping Python bindings with custom JAX frontends. Note that this C/C++ to JAX interoperability is currently limited to CPU.
For example, one may call these alternate backends for the spherical harmonic transform by:
# Forward SSHT spherical harmonic transform
flm = s2fft.forward(f, L, sampling="mw", method="jax_ssht")
# Forward HEALPix spherical harmonic transform
flm = s2fft.forward(f, L, nside=nside, sampling="healpix", method="jax_healpy")
All of these JAX frontends supports out of the box reverse mode automatic differentiation,
and under the hood is simply linking to the C/C++ packages you are familiar with. In this
way S2fft enhances existing packages with gradient functionality for modern scientific computing or machine learning
applications!
For further details on usage see the associated notebooks.
Benchmarks ⏱️
A suite of benchmark functions for both the on-the-fly and precompute versions of the spherical harmonic and Wigner transforms are available in the benchmarks directory, along with utilities for running the benchmarks and plotting the results.
Contributors ✨
Thanks goes to these wonderful people (emoji key):
We encourage contributions from any interested developers. A simple first addition could be adding support for more spherical sampling patterns!
Attribution 📚
Should this code be used in any way, we kindly request that the following article is referenced. A BibTeX entry for this reference may look like:
@article{price:s2fft,
author = "Matthew A. Price and Jason D. McEwen",
title = "Differentiable and accelerated spherical harmonic and Wigner transforms",
journal = "Journal of Computational Physics",
year = "2024",
volume = "510",
pages = "113109",
eprint = "arXiv:2311.14670",
doi = "10.1016/j.jcp.2024.113109"
}
You might also like to consider citing our related papers on which this code builds:
@article{mcewen:fssht,
author = "Jason D. McEwen and Yves Wiaux",
title = "A novel sampling theorem on the sphere",
journal = "IEEE Trans. Sig. Proc.",
year = "2011",
volume = "59",
number = "12",
pages = "5876--5887",
eprint = "arXiv:1110.6298",
doi = "10.1109/TSP.2011.2166394"
}
@article{mcewen:so3,
author = "Jason D. McEwen and Martin B{\"u}ttner and Boris ~Leistedt and Hiranya V. Peiris and Yves Wiaux",
title = "A novel sampling theorem on the rotation group",
journal = "IEEE Sig. Proc. Let.",
year = "2015",
volume = "22",
number = "12",
pages = "2425--2429",
eprint = "arXiv:1508.03101",
doi = "10.1109/LSP.2015.2490676"
}
License 📝
We provide this code under an MIT open-source licence with the hope that it will be of use to a wider community.
Copyright 2023 Matthew Price, Jason McEwen and contributors.
S2FFT is free software made available under the MIT License. For
details see the LICENCE.txt file.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distributions
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file s2fft-1.4.0.tar.gz.
File metadata
- Download URL: s2fft-1.4.0.tar.gz
- Upload date:
- Size: 22.8 MB
- Tags: Source
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
b84c0c2bb0c3dfabe3431360bf90224705554e92966ab87e92affc0fe8f956ba
|
|
| MD5 |
793b3a604c68aafb754187b1bb3e5629
|
|
| BLAKE2b-256 |
0260ac5914b6a5fce9df03d4c74eeeda9338c83eb3468fd856a08ea998b7656f
|
Provenance
The following attestation bundles were made for s2fft-1.4.0.tar.gz:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0.tar.gz -
Subject digest:
b84c0c2bb0c3dfabe3431360bf90224705554e92966ab87e92affc0fe8f956ba - Sigstore transparency entry: 943895062
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:
File details
Details for the file s2fft-1.4.0-cp314-cp314t-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl.
File metadata
- Download URL: s2fft-1.4.0-cp314-cp314t-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl
- Upload date:
- Size: 138.6 kB
- Tags: CPython 3.14t, manylinux: glibc 2.24+ x86-64, manylinux: glibc 2.28+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
9ac7d4cee989d1e5d5724ec4bfd8259bade430c30bf916e5955548b541ba0b73
|
|
| MD5 |
06c4add3b63c44d523c1a57c2a97a3b0
|
|
| BLAKE2b-256 |
2cb677f99f38bb0f09bf85f7b3667015941d003ecd880060955c1f6ea9edeef6
|
Provenance
The following attestation bundles were made for s2fft-1.4.0-cp314-cp314t-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0-cp314-cp314t-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl -
Subject digest:
9ac7d4cee989d1e5d5724ec4bfd8259bade430c30bf916e5955548b541ba0b73 - Sigstore transparency entry: 943895069
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:
File details
Details for the file s2fft-1.4.0-cp314-cp314t-macosx_11_0_arm64.whl.
File metadata
- Download URL: s2fft-1.4.0-cp314-cp314t-macosx_11_0_arm64.whl
- Upload date:
- Size: 130.3 kB
- Tags: CPython 3.14t, macOS 11.0+ ARM64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
647edd6533035283e38567b8200937064e4e1fda3bad68f43c5c3259732816db
|
|
| MD5 |
f9a52208ddae29294634878680e263e6
|
|
| BLAKE2b-256 |
531089793a12ecda9473651c4e8f395e9601fae02081e1f18e9b4af8c9035d85
|
Provenance
The following attestation bundles were made for s2fft-1.4.0-cp314-cp314t-macosx_11_0_arm64.whl:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0-cp314-cp314t-macosx_11_0_arm64.whl -
Subject digest:
647edd6533035283e38567b8200937064e4e1fda3bad68f43c5c3259732816db - Sigstore transparency entry: 943895075
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:
File details
Details for the file s2fft-1.4.0-cp312-abi3-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl.
File metadata
- Download URL: s2fft-1.4.0-cp312-abi3-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl
- Upload date:
- Size: 137.5 kB
- Tags: CPython 3.12+, manylinux: glibc 2.24+ x86-64, manylinux: glibc 2.28+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
60ef04398dc4481232609a11d7ba4e0a9fbe3b311bbbab5a600f058dbaa7e61c
|
|
| MD5 |
f564194753e6f9e1bdb5351168dd3a54
|
|
| BLAKE2b-256 |
bb747ec92e611283b1a559a0b2e535621985b66c6c48128207887a999448e472
|
Provenance
The following attestation bundles were made for s2fft-1.4.0-cp312-abi3-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0-cp312-abi3-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl -
Subject digest:
60ef04398dc4481232609a11d7ba4e0a9fbe3b311bbbab5a600f058dbaa7e61c - Sigstore transparency entry: 943895063
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:
File details
Details for the file s2fft-1.4.0-cp312-abi3-macosx_11_0_arm64.whl.
File metadata
- Download URL: s2fft-1.4.0-cp312-abi3-macosx_11_0_arm64.whl
- Upload date:
- Size: 129.4 kB
- Tags: CPython 3.12+, macOS 11.0+ ARM64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
c5f984316b81fdfdcaffcfdcb2ba9bdf70b2c25d3ef23313f8123d360f566833
|
|
| MD5 |
4e598a7b83c54fd4981aa69939c93179
|
|
| BLAKE2b-256 |
0d1f39fc6e6f69a0c1f7de40f2defaa1ef80de33c66814b98506d850f18b0c18
|
Provenance
The following attestation bundles were made for s2fft-1.4.0-cp312-abi3-macosx_11_0_arm64.whl:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0-cp312-abi3-macosx_11_0_arm64.whl -
Subject digest:
c5f984316b81fdfdcaffcfdcb2ba9bdf70b2c25d3ef23313f8123d360f566833 - Sigstore transparency entry: 943895077
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:
File details
Details for the file s2fft-1.4.0-cp311-cp311-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl.
File metadata
- Download URL: s2fft-1.4.0-cp311-cp311-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl
- Upload date:
- Size: 138.1 kB
- Tags: CPython 3.11, manylinux: glibc 2.24+ x86-64, manylinux: glibc 2.28+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
42a521700d4793f7ac8a2308233e561065567f03c98b91747c508f02ce4a2cd4
|
|
| MD5 |
f30594304f817920723cf5ce82733369
|
|
| BLAKE2b-256 |
9bbb0ca3beb35de790ac66a98c5ea1f8043125f9b331af1b0c519b1e62e0e342
|
Provenance
The following attestation bundles were made for s2fft-1.4.0-cp311-cp311-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0-cp311-cp311-manylinux_2_24_x86_64.manylinux_2_28_x86_64.whl -
Subject digest:
42a521700d4793f7ac8a2308233e561065567f03c98b91747c508f02ce4a2cd4 - Sigstore transparency entry: 943895080
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:
File details
Details for the file s2fft-1.4.0-cp311-cp311-macosx_11_0_arm64.whl.
File metadata
- Download URL: s2fft-1.4.0-cp311-cp311-macosx_11_0_arm64.whl
- Upload date:
- Size: 129.8 kB
- Tags: CPython 3.11, macOS 11.0+ ARM64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
739544caa6eb7cfa34700c1cc55634739601d8557819e88c7addce9fad93c7c5
|
|
| MD5 |
729f0a1246f67816a2fe9dec7ba547eb
|
|
| BLAKE2b-256 |
f9bc7175a55f8aa4c0e36fbe5c33b2d129309fe6025a0ad4a683e85c80cc45e6
|
Provenance
The following attestation bundles were made for s2fft-1.4.0-cp311-cp311-macosx_11_0_arm64.whl:
Publisher:
build.yml on astro-informatics/s2fft
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
s2fft-1.4.0-cp311-cp311-macosx_11_0_arm64.whl -
Subject digest:
739544caa6eb7cfa34700c1cc55634739601d8557819e88c7addce9fad93c7c5 - Sigstore transparency entry: 943895067
- Sigstore integration time:
-
Permalink:
astro-informatics/s2fft@e140536880fc53081a98156fb0245d9d197d1e5d -
Branch / Tag:
refs/tags/v1.4.0 - Owner: https://github.com/astro-informatics
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
build.yml@e140536880fc53081a98156fb0245d9d197d1e5d -
Trigger Event:
release
-
Statement type:





































