Segmented Least Squares
Project description
seglines
Compute segmented least squares for a dataset. Probably assumes that X = 1...N or something.
$ seglines 10 data.csv --plot
opt = 70.19
segment 1: 0 (1.330) 13 (13.880) f(x) = 1.009·x + 1.693
segment 2: 14 (1.340) 27 (14.190) f(x) = 0.997·x + -11.887
segment 3: 28 (3.350) 41 (15.760) f(x) = 0.987·x + -25.083
segment 4: 42 (3.420) 55 (17.630) f(x) = 0.991·x + -37.058
segment 5: 56 (5.160) 69 (18.600) f(x) = 0.949·x + -46.523
segment 6: 70 (3.870) 83 (17.660) f(x) = 0.973·x + -63.211
segment 7: 84 (5.930) 97 (17.490) f(x) = 0.977·x + -76.830
segment 8: 98 (5.210) 111 (17.590) f(x) = 0.897·x + -82.366
segment 9: 112 (3.810) 125 (16.410) f(x) = 0.963·x + -102.544
segment 10: 126 (16.780) 139 (3.190) f(x) = -1.036·x + 147.696
Install
pip install seglines
Depends only on numpy. When using --plot, we also need matplotlib.
Usage
There is a --help option: seglines --help
Use seglines L data.csv where L is the number of segments you want to segmentize into.
In case you want to generate an L-segmented linear dataset, use
seglines --generate 5 10 > data.csv
and then
seglines 5 data.csv
This will output the segments, e.g.
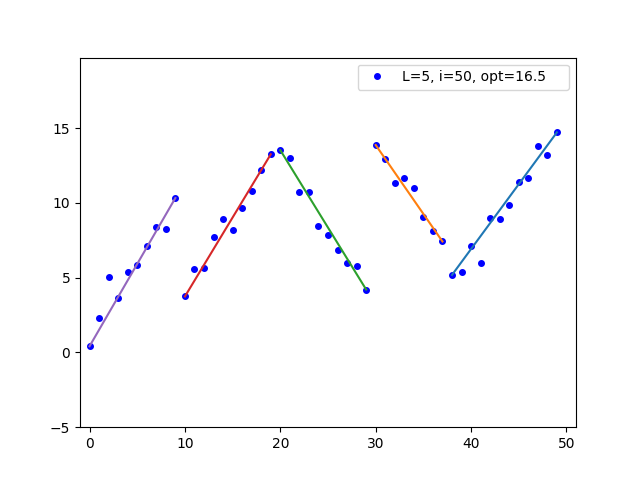
opt = 16.49
segment 1: 0 (0.410) 9 (10.330) f(x) = 0.961·x + 1.355
segment 2: 10 (3.750) 19 (13.260) f(x) = 0.987·x + -5.741
segment 3: 20 (13.530) 29 (4.210) f(x) = -1.031·x + 33.960
segment 4: 30 (13.880) 37 (7.420) f(x) = -0.913·x + 41.254
segment 5: 38 (5.190) 49 (14.720) f(x) = 0.904·x + -29.629
To create a plot of the dataset, add --plot:
seglines 5 data.csv --plot
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
seglines-0.0.5.tar.gz
(4.8 kB
view details)
File details
Details for the file seglines-0.0.5.tar.gz.
File metadata
- Download URL: seglines-0.0.5.tar.gz
- Upload date:
- Size: 4.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.8.10
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
54392c8598afd9c83f943b1d3dc3ce93e030e0585c6343002270ca6fb5c33fb4
|
|
| MD5 |
3760f38a5c7293a26b47f2e7aeaece87
|
|
| BLAKE2b-256 |
992df6ef0fb44b2766d9e3a459705ccc1d44b29d3760eddd012719765b65d72c
|