Shenfun -- Automated Spectral-Galerkin framework
Project description





Description
Shenfun is a high performance computing platform for solving partial differential equations (PDEs) by the spectral Galerkin method. The user interface to shenfun is very similar to FEniCS, but applications are limited to multidimensional tensor product grids, using either Cartesian or curvilinear grids (e.g., but not limited to, polar, cylindrical, spherical or parabolic). The code is parallelized with MPI through the mpi4py-fft package.
Shenfun enables fast development of efficient and accurate PDE solvers (spectral order and accuracy), in the comfortable high-level Python language. The spectral accuracy is ensured by using high-order global orthogonal basis functions (Fourier, Legendre, Chebyshev first and second kind, Ultraspherical, Jacobi, Laguerre and Hermite), as opposed to finite element codes that are using low-order local basis functions. Efficiency is ensured through vectorization (Numpy), parallelization (mpi4py) and by moving critical routines to Cython or Numba. Shenfun has been used to run turbulence simulations (Direct Numerical Simulations) on thousands of processors on high-performance supercomputers, see the spectralDNS repository.
The demo folder contains several examples for the Poisson, Helmholtz and Biharmonic equations. For extended documentation and installation instructions see ReadTheDocs. For interactive demos, see the jupyter book. Note that shenfun currently comes with the possibility to use two non-periodic directions (see biharmonic demo), and equations may be solved coupled and implicit (see MixedPoisson.py).
Note that shenfun works with curvilinear coordinates. For example, it is possible to solve equations on a sphere (using spherical coordinates), on the surface of a torus, on a Möbius strip or along any curved line in 2D/3D. Actually, any new coordinates may be defined by the user as long as the coordinates lead to a system of equations with separable coefficients. After defining new coordinates, operators like div, grad and curl work automatically with the new curvilinear coordinates. See also this notebook on the sphere or an illustration of the vector Laplacian.
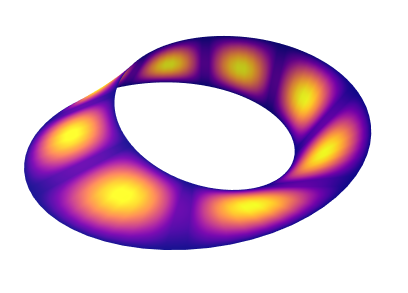
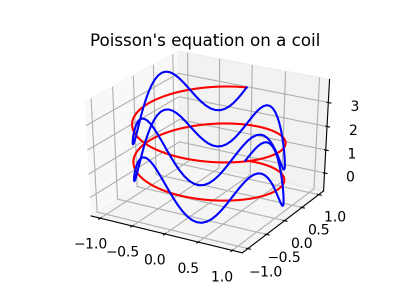
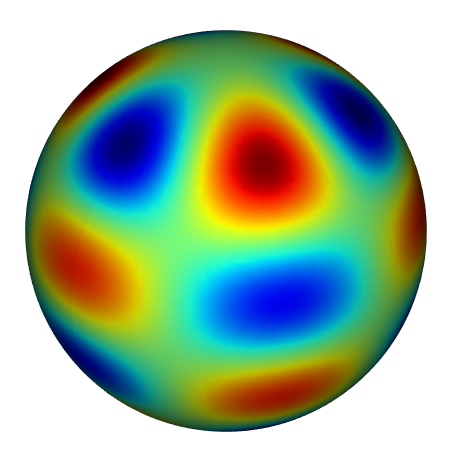
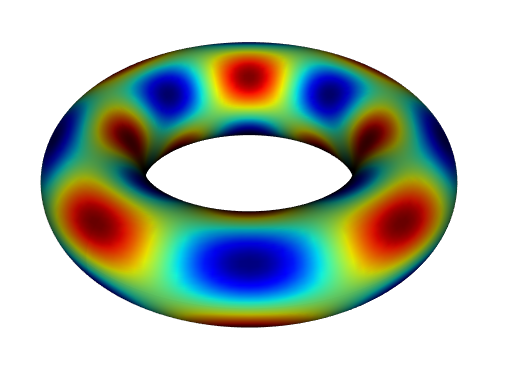
For a more psychedelic experience, have a look at the simulation of the Ginzburg-Landau equation on the sphere (click for Youtube-video):

Shenfun can also be used to approximate analytical functions with global spectral basis functions, and to integrate over highly complex domains, like the seashell below, see this demo.

Some recent papers using Shenfun
Effective control of two-dimensional Rayleigh–Bénard convection: Invariant multi-agent reinforcement learning is all you need C. Vignon, J. Rabault, J. Vasanth, F. Alcántara-Ávila, M. Mortensen, R. Vinuesa, Physics of Fluids 35, 065146 (2023)
Solving Partial Differential Equations with Equivariant Extreme Learning Machines, H. Harder, J. Rabault, R. Vinuesa, M. Mortensen, S. Peitz. preprint (2024)
A global spectral-Galerkin investigation of a Rayleigh–Taylor instability in plasma using an MHD–Boussinesq model A. Piterskaya, Wojciech J. Miloch, M. Mortensen, AIP Advances 13, 105319 (2023)
A Generic and Strictly Banded Spectral Petrov–Galerkin Method for Differential Equations with Polynomial Coefficients M. Mortensen, SIAM J. on Scientific Computing, 45, 1, A123-A146, (2023)
Variance representations and convergence rates for data-driven approximations of Koopman operators F. M. Philipp, M. Schaller, S. Boshoff, S. Peitz, F. Nüske, K. Worthmann, preprint (2024)
Partial observations, coarse graining and equivariance in Koopman operator theory for large-scale dynamical systems, S. Peitz, H. Harder, F. Nüske, F. Philipp, M. Schaller, K. Worthmann, preprint (2024)
Koopman-Based Surrogate Modelling of Turbulent Rayleigh-Bénard Convection T. Markmann, M. Straat, B. Hammer, preprint (2024)
Shenfun: High performance spectral Galerkin computing platform, M. Mortensen, Journal of Open Source Software, 3(31), 1071 (2018)
Installation
Shenfun can be installed using either pip or conda, see installation chapter on readthedocs.
Dependencies
Try it in a codespace
The easiest way to try out shenfun is to create your own codespace. Press the green codespace button on this page and wait for a couple of minutes while everything in environment.yml gets installed. Then write in the terminal of the codespace editor:
source activate shenfun echo -e "PYTHONPATH=/workspaces/shenfun" > .env export PYTHONPATH=/workspaces/shenfun
and you are set to run any of the demo programs, or for example try to follow the detailed instructions in the documentation. We assume that you know how to run a Python program. Please note that if you want to use for example IPython or Jupyter in the codespace, then these need to be installed into the shenfun environment.
Contact
For comments, issues, bug-reports and requests, please use the issue tracker of the current repository, or see How to contribute? at readthedocs. Otherwise the principal author can be reached at:
Mikael Mortensen mikaem at math.uio.no https://mikaem.github.io/ Department of Mathematics University of Oslo Norway
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file shenfun-4.2.2.tar.gz.
File metadata
- Download URL: shenfun-4.2.2.tar.gz
- Upload date:
- Size: 336.0 kB
- Tags: Source
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
41b01b43aff63c55dfe32d2b70910998a8af8b54f2722d6072f3ceec596b6df1
|
|
| MD5 |
64f6ca803a7ea3b3d4362d27471dca51
|
|
| BLAKE2b-256 |
e4765004d4522074cb7fb7b6664dc35b80b8e8ca0dca31243385b94396ebbefc
|
Provenance
The following attestation bundles were made for shenfun-4.2.2.tar.gz:
Publisher:
release.yml on spectralDNS/shenfun
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
shenfun-4.2.2.tar.gz -
Subject digest:
41b01b43aff63c55dfe32d2b70910998a8af8b54f2722d6072f3ceec596b6df1 - Sigstore transparency entry: 153075612
- Sigstore integration time:
-
Permalink:
spectralDNS/shenfun@13648858780e3fb710c0ada3196e0aa7d6e2de87 -
Branch / Tag:
refs/tags/4.2.2 - Owner: https://github.com/spectralDNS
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
release.yml@13648858780e3fb710c0ada3196e0aa7d6e2de87 -
Trigger Event:
release
-
Statement type:










