Refreshing hypothesis testing in python!
Project description
 spearmint
spearmint 
Refreshing hypothesis testing in python
Features
- Offers a simple API for running, visualizing, and interpreting statistically-rigorous hypothesis tests with none of the hastle of jumping between various statistical or visualization packages.
- Supports most common variable types used in AB Tests inlcuding, continuous, binary/proportions, counts/rates data.
- Implements many Frequentist, Bayesian, and Bootstrap inference methods
- Supports multiple customizations:
- Custom metric definitions
- Simple Bayesian prior definition
- Easily extendable to support new inference methods
Installation
Requirements
spearminthas been tested onpython>=3.10.
Install via pip
pip install spearmint
If you plan to run your analyses in jupyterlab, you can add the notebook option
pip install spearmint[notebook]
Install via conda (WIP)
conda install -c conda-forge spearmint # not yet on conda-forge
Install from source
If you would like to contribute to spearmint, then you'll want to install from source (or use the -e flag when installing from PyPI):
mkdir /PATH/TO/LOCAL/SPEARMINT && cd /PATH/TO/LOCAL/SPEARMINT
git clone git@github.com:dustinstansbury/spearmint.git
cd spearmint
pip install -e .
Basics Usage
Observations data
Spearmint takes as input a pandas DataFrame containing experiment observations data. Each record represents an observation/trial recorded in the experiment and has the following columns:
- One or more
treatmentcolumns: each treatment column contains two or more distinct, discrete values that are used to identify the different groups in the experiment. - One or more
metriccolumns: these are the values associated with each observation that are used to compare groups in the experiment. - Zero or more
attributescolumns: these define additional discrete properties assigned to the observations. These attributes can be used to perform segmentation across groups.
To demonstrate, let's generate some artificial experiment observations data. The metric column in our dataset will be a series of binary outcomes (i.e. True/False). This binary metric is analogous to conversion or success in AB testing.
from spearmint.utils import generate_fake_observations
"""Generate binary demo data"""
experiment_observations = generate_fake_observations(
distribution="bernoulli",
n_treatments=3,
n_attributes=4,
n_observations=120,
random_seed=123
)
experiment_observations.head()
These fake observations are simulated from a different Bernoulli distributions, each distribution being associated with the three treatements (named "A", "B", or "C"), and each distrubition having increasing average probability of conversion. The simulated data also contains four attribute columns, named attr_*, that can potentially be used for segmentation.
id treatment attr_0 attr_1 attr_2 attr_3 metric
0 0 C A0a A1b A2a A3a True
1 1 B A0a A1b A2a A3b True
2 2 C A0a A1a A2a A3b True
3 3 C A0a A1a A2a A3b True
4 4 A A0a A1b A2a A3a True
Running an AB test in spearmint is as easy as ✨1-2-3✨:
-
- Initialize an
Experiment, which holds the raw observations, and any metadata associated with an AB experiment.
- Initialize an
-
- Define the
HypothesisTest, which declares the configuration of the statistical inference procedure.
- Define the
-
- Run the
HypothesisTestagainst theExperimentand interpret the resultingInferenceResults.InferenceResults, hold the parameter estimates of the inference procedure, and are used to summarize, visualize, and save the results of the hypothesis test.
- Run the
Example Workflow
Below we demonstrate how to run a hypothesis test analysis on the fake observations data generated in a 1-2-3 fashion.
1. Initialize the Experiment
from spearmint import Experiment
experiment = Experiment(data=experiment_observations)
Since the metric column in the simulated observations are binary (i.e. True/False), we'll essentially be running a test for the difference in success rates--i.e. what's the probability of observing a True--between two groups. This is analogous to running an AB experiment that aims to compare conversion rates (e.g. clicking a CTA, opening an email, signing up for a service, etc.) between a control and a variation group.
2. Define the HypothesisTest
Here, we test the hypothesis that that the conversion rate for treatment group 'C' (the variation) is 'larger' than for the treatment group 'A' (the control, or reference group).
from spearmint import HypothesisTest
ab_test = HypothesisTest(
treatment='treatment',
metric='metric',
control='A',
variation='C',
hypothesis='larger',
# variable_type='binary', # inferred from `metric` values
# inference_method='frequentist' # default
)
3. Run the test and interpret the InferenceResults
Here, we run our HypothesisTest with an acceptable Type I error rate of alpha=0.05
ab_test_results = experiment.run_test(ab_test, alpha=0.05)
assert ab_test.variable_type == 'binary' # check that correct variable_type inferred
assert ab_test_results.accept_hypothesis
"""Display test results to stdout"""
ab_test_results.display()
The test results displays two tables. The first table gives a summary of the observed samples from the control ("A") and variation ("C") groups. This Samples Comparison table gives the number of samples, the mean, variance, and standard error of the mean estimation, as well as the difference in mean estimates between the variation and control groups.
Samples Comparison
┏━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━┓
┃ ┃ A ┃ C ┃
┡━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━┩
│ Samples │ 35 │ 44 │
│ Mean │ 0.4286 │ 0.75 │
│ Standard Error │ (0.2646, 0.5925) │ (0.6221, 0.8779) │
│ Variance │ 0.2449 │ 0.1875 │
│ Delta │ │ 0.3214 │
└────────────────┴──────────────────┴──────────────────┘
Proportions Delta Results
┌────────────────────┬──────────────────┐
│ Delta │ 0.3214 │
│ Delta CI │ (0.1473, inf) │
│ Delta-relative │ 0.75 % │
│ Delta-relative CI │ (34.3703, inf) % │
│ Delta CI %-tiles │ (0.05, inf) │
│ Effect Size │ 0.6967 │
│ alpha │ 0.05 │
│ Power │ 0.92 │
│ Variable Type │ binary │
│ Inference Method │ frequentist │
│ Test statistic (z) │ 3.47 │
│ p-value │ 0.0003 │
│ Hypothesis │ C is larger │
│ Accept Hypothesis │ True │
└────────────────────┴──────────────────┘
The second table shows a summary of the results from the hypothesis test inference procedure.
Interpreting inference results
We first see that this test uses a Proportions Delta inference procedure. Each inference procedure will test for the Delta in expected value between the two groups. For "binary" variables, this expected value is the proportionality or average conversion rate. For "continuous" variables the expecteted value is the mean, for "count" variables the expected value will be expected number of events observed.
We see that there is a larger proportionality (e.g. conversion rate) for the variation group 'C', when compared to that of the control group 'A'. Specifically there is a Delta of 0.32 in expected value between the two groups.
The results also report confidence intervals CI around the Delta estimates. Since the hypothesis is "larger", the lower bound of the CI is $1-\alpha$ %, while the upper bound of the condifence intervals is $\infty$; these bounds are given by Delta CI %-tiles.
Along with absolute Delta, we report the Relative Delta, here a 75% relative increase. Delta Relative estimates also have associated CIs.
The size of the Delta in proportionality is moderately large, as indicated by an effect size of 0.70. This test also results in a p-value of 0.0003, which is lower than the prescribed $\alpha=$ 0.05. Thus the Hypothesis test declares that the hypothesis that 'C is larger' should be accepted.
Visualizing InferenceResults
In addition to .display()ing the test results to the console, we can .visualize() the results.
ab_test_results.visualize()
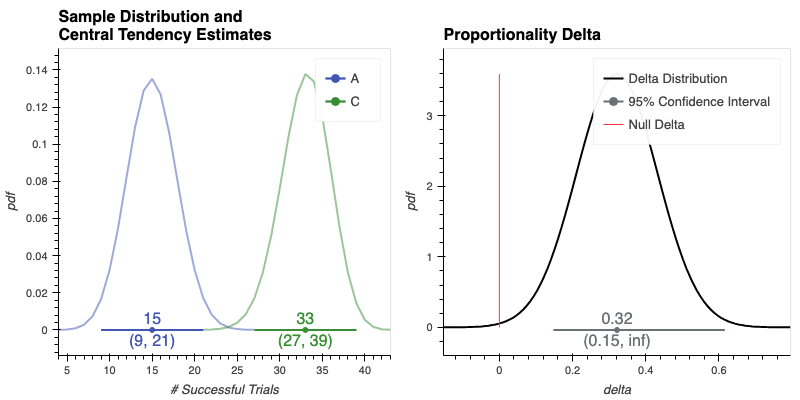
The left plot shows each Samples's estimated parametric distribution, as well as the estimates of group central tendency and 95% Confidence Intervals (CIs) around those estiates (plotted as intervals along the x-axis). Non-overlapping distributions and CIs provides strong visual evidence that the difference between the two groups' central tendencies is statistically significant.
The right plot shows the Delta distribution over the difference in those estimated sample distributions, along with 95% CIs. Delta CIs greater than zero give further visual evidence that the difference in the two samples is statistically significant.
💡 NOTE
For "binary", "frequentist" tests--i.e. Proportions Delta tests--we display the inference results for the observed Samples (i.e. the left ab_test_results.visualize() plot) as binomial distributions, giving the distribution over the expected number of successful trials given the total number observations and the number of True/False trials per group.
Additional Documentation and Tutorials
For more details of using spearmint's API see the Spearmint Basics Tutorial, or try running it in Google Collab
CHANGELOG
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file spearmint-0.0.2.tar.gz.
File metadata
- Download URL: spearmint-0.0.2.tar.gz
- Upload date:
- Size: 587.4 kB
- Tags: Source
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/4.0.2 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
b0a13476250d09ea6ddc9807352a6d922a86bab45a7606a6d328e5c539ed5a5d
|
|
| MD5 |
42b7067567a36bf420adf3d5abe39314
|
|
| BLAKE2b-256 |
2885c083ede997e7032b4ed7d6ec8ed587a1eac24a980c9469f183bcabfbf977
|
File details
Details for the file spearmint-0.0.2-py3-none-any.whl.
File metadata
- Download URL: spearmint-0.0.2-py3-none-any.whl
- Upload date:
- Size: 67.2 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/4.0.2 CPython/3.11.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
890a9b4c6386402945d68ad69e50825999886373b8f37e00eddfeaddc9097816
|
|
| MD5 |
ba15184af20f7e1fc2acd8764f872409
|
|
| BLAKE2b-256 |
9f619dd6e6d0b37a1eff8ff00473bf0f0dbc1f3abd4af1fbf762d983e99609e2
|


















