toolbox for higher spin and symmetrization
Project description
toolbox for higher spin and symmetrization






spheres provides tools for dealing with higher spin systems and for symmetrized quantum circuits. Among other things, we provide implementations of:
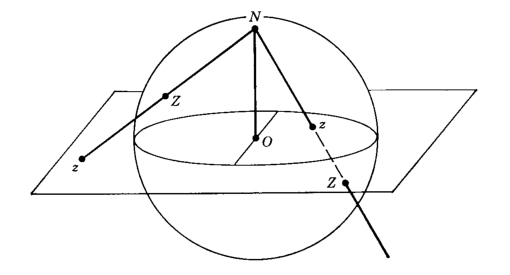
The “Majorana stars” representation of a spin-j state as a degree-2j complex polynomial defined on the extended complex plane (the Riemann sphere). The eponymous stars are the 2j roots of this polynomial and each can be interpreted as a quantum of angular momentum contributing 1/2 in the specified direction. This polynomial can be defined in terms of the components of a |j, m> vector or in terms of a spin coherent wavefunction <-xyz|psi>, where |psi> is the spin state and <-xyz| is the adjoint of a spin coherent state at the point antipodal to xyz.
The “symmetrized spinors” representation of a spin-j state as 2j symmetrized spin-1/2 states (aka qubits). Indeed, the basis states of 2j symmetrized qubits are in 1-to-1 relation to the |j, m> basis states of a spin-j. Such a representation is naturally useful for simulating spin-j states on a qubit based quantum computer, and we provide circuits for preparing such states.
The “Schwinger oscillator” representation of a spin-j state as the total energy 2j subspace of two quantum harmonic oscillators. Indeed, the full space of the two oscillators furnishes a representation of spin with a variable j value: a superposition of j values. This construction can be interpreted as the “second quantization” of qubit, and is appropriate for implementation of photonic quantum computers.
Everything is accompanied by 3D visualizations thanks to vpython (and matplotlib) and interfaces to popular quantum computing libraries from qutip to StrawberryFields.
Finally, we provide tools for implementing a form of quantum error correction or “stablization” by harnessing the power of symmetrization. We provide automatic generation of circuits which perform a given quantum experiment multiple times in parallel while periodically projecting them all jointly into the symmetric subspace, which in principle increases the reliability of the computation under noisy conditions.
spheres is a work in progress! Beware!
Get started:
from spheres import *
vsphere = MajoranaSphere(qt.rand_ket(3))
vsphere.evolve(qt.rand_herm(3))Check out the documentation.
For more information and reference material, including jupyter notebooks, visit heyredhat.github.io.
Special thanks to the Quantum Open Source Foundation.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file spheres-0.3.0.9.tar.gz.
File metadata
- Download URL: spheres-0.3.0.9.tar.gz
- Upload date:
- Size: 43.2 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.3.0 pkginfo/1.7.0 requests/2.25.1 setuptools/49.2.1 requests-toolbelt/0.9.1 tqdm/4.56.0 CPython/3.8.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
9dcbb15c5774968a1b5d723e27d627a9ec03dad9e4c23cef992b3bc62729f094
|
|
| MD5 |
5fc0c839dcdfacf9fc282cc39b4d33b3
|
|
| BLAKE2b-256 |
7001ed4dce72365ced01b78e07ef6aea6d92e3b4516b5626e2c4e423a4b1c111
|
File details
Details for the file spheres-0.3.0.9-py3-none-any.whl.
File metadata
- Download URL: spheres-0.3.0.9-py3-none-any.whl
- Upload date:
- Size: 63.6 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.3.0 pkginfo/1.7.0 requests/2.25.1 setuptools/49.2.1 requests-toolbelt/0.9.1 tqdm/4.56.0 CPython/3.8.6
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
3c0a1bb01fc7f78526cc8d379d07545c68c1e7a0f81ed8a9eb99ef0d9d113c16
|
|
| MD5 |
a54418ce3dee46a99247cc2d1a60416a
|
|
| BLAKE2b-256 |
2dd1a62dd1f4153601e2eed7546069169b4db72adcdb03258662040da5092e37
|










