a symbolic finite element definition library
Project description
| Badges | |
|---|---|
| Documentation |  |
| Testing & coverage |     |
| Packages |   |
| Paper |  |
Symfem is a symbolic finite element definition library, that can be used to symbolically evaluate the basis functions of a finite element space. Symfem can:
- Symbolically compute the basis functions of a wide range of finite element spaces
- Symbolically compute derivatives and vector products and substitute values into functions
- Allow the user to define their own element using the Ciarlet definition of a finite element
- Be used to verify that the basis functions of a given space have some desired properties
You can find details of recent changes to Symfem in the changelog.
Installing Symfem
Installing from source using pip
Symfem can be installed by downloading the GitHub repo and running:
pip3 install .
You may also use -e to install in editable mode:
pip3 install -e .
Installing from PyPI using pip
The latest release of Symfem can be installed by running:
pip3 install symfem
Installing using conda
The latest release of Symfem can be installed by running:
conda install -c conda-forge symfem
Testing Symfem
To run the Symfem unit tests, clone the repository and run:
python3 -m pytest test/
You may instead like to run the following, as this will skip the slowest tests.
python3 -m pytest test/ --speed fast
Using Symfem
Finite elements can be created in Symfem using the symfem.create_element()
function. For example, some elements are created in the following snippet:
import symfem
lagrange = symfem.create_element("triangle", "Lagrange", 1)
rt = symfem.create_element("tetrahedron", "Raviart-Thomas", 2)
nedelec = symfem.create_element("triangle", "N2curl", 1)
qcurl = symfem.create_element("quadrilateral", "Qcurl", 2)
The basis functions of an element can be obtained by calling get_basis_functions():
lagrange = symfem.create_element("triangle", "Lagrange", 1)
print(lagrange.get_basis_functions())
[-x - y + 1, x, y]
Each basis function will be a Sympy symbolic expression.
Derivative of these basis functions can be computed using the functions in
symfem.functions.
The function map_to_cell can be used to map the basis functions of a finite element
to a non-default cell:
lagrange = symfem.create_element("triangle", "Lagrange", 1)
print(lagrange.get_basis_functions())
print(lagrange.map_to_cell([(0,0), (2, 0), (2, 1)]))
[-x - y + 1, x, y]
[1 - x/2, x/2 - y, y]
Further documentation
More detailed documentation of the latest release version of Symfem can be found on
Read the Docs. A series of example uses
of Symfem can be found in the demo folder or viewed on
Read the Docs.
Details of the definition of each element can be found on DefElement alongside Symfem snippets for creating the element.
Getting help
You can ask questions about using Symfem by using GitHub Discussions. Bugs can be reported using the GitHub issue tracker.
Contributing to Symfem
Reporting bugs
If you find a bug in Symfem, please report it on the issue tracker.
Suggesting enhancements
If you want to suggest a new feature or an improvement of a current feature, you can submit this on the issue tracker.
Adding a new element
If you want to add a new element to Symfem, take a look at the Adding an element guide.
Submitting a pull request
If you want to directly submit code to Symfem, you can do this by forking the Symfem repo, then submitting a pull request. If you want to contribute, but are unsure where to start, have a look at the issues labelled "good first issue".
On opening a pull request, unit tests and flake8 style checks will run. You can click on these in the pull request to see where (if anywhere) there are errors in your code.
Code of conduct
We expect all our contributors to follow the Contributor Covenant. Any unacceptable behaviour can be reported to Matthew (symfem@mscroggs.co.uk).
Available cells and elements
Interval
The reference interval has vertices (0,) and (1,). Its sub-entities are numbered as follows.
List of supported elements
- Bernstein (alternative names: Bernstein-Bezier)
- bubble
- dPc
- enriched Galerkin (alternative names: EG)
- Hermite
- Lagrange (alternative names: P)
- Morley-Wang-Xu (alternative names: MWX)
- P1-iso-P2 (alternative names: P2-iso-P1, iso-P2 P1)
- serendipity (alternative names: S)
- Taylor (alternative names: discontinuous Taylor)
- vector Lagrange (alternative names: vP)
- Wu-Xu
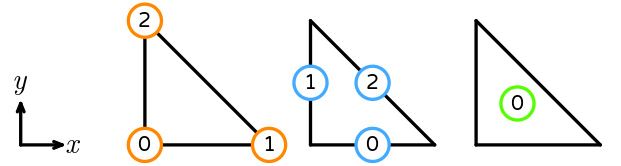
Triangle
The reference triangle has vertices (0, 0), (1, 0), and (0, 1). Its sub-entities are numbered as follows.
List of supported elements
- Alfeld-Sorokina (alternative names: AS)
- Argyris
- Arnold-Winther (alternative names: AW, conforming Arnold-Winther)
- Bell
- Bernardi-Raugel
- Bernstein (alternative names: Bernstein-Bezier)
- Brezzi-Douglas-Fortin-Marini (alternative names: BDFM)
- Brezzi-Douglas-Marini (alternative names: BDM, N2div)
- bubble
- bubble enriched Lagrange
- bubble enriched vector Lagrange
- conforming Crouzeix-Raviart (alternative names: conforming CR)
- Crouzeix-Raviart (alternative names: CR, Crouzeix-Falk, CF)
- enriched Galerkin (alternative names: EG)
- enriched vector Galerkin (alternative names: locking-free enriched Galerkin, LFEG)
- Fortin-Soulie (alternative names: FS)
- Gopalakrishnan-Lederer-Schoberl (alternative names: GLS)
- Guzman-Neilan first kind (alternative names: Guzman-Neilan)
- Guzman-Neilan second kind
- Hellan-Herrmann-Johnson (alternative names: HHJ)
- Hermite
- Hsieh-Clough-Tocher (alternative names: Clough-Tocher, HCT, CT)
- Kong-Mulder-Veldhuizen (alternative names: KMV)
- Lagrange (alternative names: P)
- Mardal-Tai-Winther (alternative names: MTW)
- matrix Lagrange
- Morley
- Morley-Wang-Xu (alternative names: MWX)
- Nedelec (alternative names: Nedelec1, N1curl)
- Nedelec2 (alternative names: N2curl)
- nonconforming Arnold-Winther (alternative names: nonconforming AW)
- P1 macro
- P1-iso-P2 (alternative names: P2-iso-P1, iso-P2 P1)
- Raviart-Thomas (alternative names: RT, N1div)
- reduced Hsieh-Clough-Tocher (alternative names: rHCT)
- Regge
- symmetric matrix Lagrange
- Taylor (alternative names: discontinuous Taylor)
- transition
- vector Lagrange (alternative names: vP)
- Wu-Xu
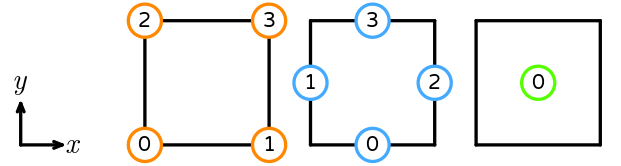
Quadrilateral
The reference quadrilateral has vertices (0, 0), (1, 0), (0, 1), and (1, 1). Its sub-entities are numbered as follows.
List of supported elements
- Arbogast-Correa (alternative names: AC, AC full, Arbogast-Correa full)
- Arnold-Boffi-Falk (alternative names: ABF)
- Bogner-Fox-Schmit (alternative names: BFS)
- Brezzi-Douglas-Fortin-Marini (alternative names: BDFM)
- bubble
- direct serendipity
- dPc
- enriched Galerkin (alternative names: EG)
- enriched vector Galerkin (alternative names: locking-free enriched Galerkin, LFEG)
- Huang-Zhang (alternative names: HZ)
- NCE (alternative names: RTCE, Qcurl, Nedelec, Ncurl)
- NCF (alternative names: RTCF, Qdiv)
- P1-iso-P2 (alternative names: P2-iso-P1, iso-P2 P1)
- Q (alternative names: Lagrange, P)
- Rannacher-Turek
- Regge
- serendipity (alternative names: S)
- serendipity Hcurl (alternative names: Scurl, BDMCE, AAE)
- serendipity Hdiv (alternative names: Sdiv, BDMCF, AAF)
- tiniest tensor (alternative names: TNT)
- tiniest tensor Hcurl (alternative names: TNTcurl)
- tiniest tensor Hdiv (alternative names: TNTdiv)
- trimmed serendipity Hcurl (alternative names: TScurl)
- trimmed serendipity Hdiv (alternative names: TSdiv)
- vector dPc
- vector Q (alternative names: vQ)
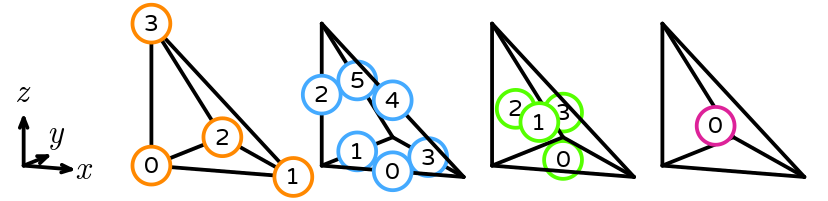
Tetrahedron
The reference tetrahedron has vertices (0, 0, 0), (1, 0, 0), (0, 1, 0), and (0, 0, 1). Its sub-entities are numbered as follows.
List of supported elements
- Bernardi-Raugel
- Bernstein (alternative names: Bernstein-Bezier)
- Brezzi-Douglas-Fortin-Marini (alternative names: BDFM)
- Brezzi-Douglas-Marini (alternative names: BDM, N2div)
- bubble
- Crouzeix-Raviart (alternative names: CR, Crouzeix-Falk, CF)
- enriched Galerkin (alternative names: EG)
- enriched vector Galerkin (alternative names: locking-free enriched Galerkin, LFEG)
- Gopalakrishnan-Lederer-Schoberl (alternative names: GLS)
- Guzman-Neilan first kind (alternative names: Guzman-Neilan)
- Guzman-Neilan second kind
- Hellan-Herrmann-Johnson (alternative names: HHJ)
- Hermite
- Kong-Mulder-Veldhuizen (alternative names: KMV)
- Lagrange (alternative names: P)
- Mardal-Tai-Winther (alternative names: MTW)
- matrix Lagrange
- Morley-Wang-Xu (alternative names: MWX)
- Nedelec (alternative names: Nedelec1, N1curl)
- Nedelec2 (alternative names: N2curl)
- Raviart-Thomas (alternative names: RT, N1div)
- Regge
- symmetric matrix Lagrange
- Taylor (alternative names: discontinuous Taylor)
- transition
- vector Lagrange (alternative names: vP)
- Wu-Xu
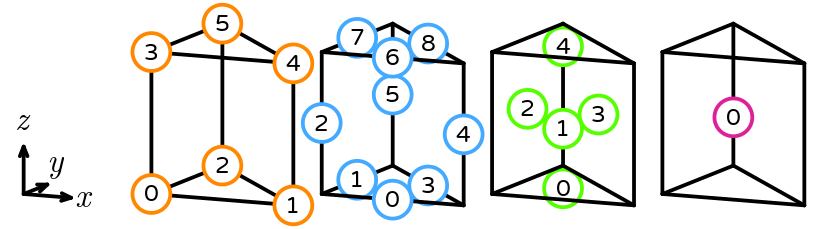
Hexahedron
The reference hexahedron has vertices (0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 1, 0), (0, 0, 1), (1, 0, 1), (0, 1, 1), and (1, 1, 1). Its sub-entities are numbered as follows.
List of supported elements
- Brezzi-Douglas-Duran-Fortin (alternative names: BDDF)
- Brezzi-Douglas-Fortin-Marini (alternative names: BDFM)
- bubble
- dPc
- enriched Galerkin (alternative names: EG)
- enriched vector Galerkin (alternative names: locking-free enriched Galerkin, LFEG)
- NCE (alternative names: RTCE, Qcurl, Nedelec, Ncurl)
- NCF (alternative names: RTCF, Qdiv)
- Q (alternative names: Lagrange, P)
- Rannacher-Turek
- Regge
- serendipity (alternative names: S)
- serendipity Hcurl (alternative names: Scurl, BDMCE, AAE)
- serendipity Hdiv (alternative names: Sdiv, BDMCF, AAF)
- tiniest tensor (alternative names: TNT)
- tiniest tensor Hcurl (alternative names: TNTcurl)
- tiniest tensor Hdiv (alternative names: TNTdiv)
- trimmed serendipity Hcurl (alternative names: TScurl)
- trimmed serendipity Hdiv (alternative names: TSdiv)
- vector dPc
- vector Q (alternative names: vQ)
Prism
The reference prism has vertices (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 0, 1), and (0, 1, 1). Its sub-entities are numbered as follows.
List of supported elements
- Lagrange (alternative names: P)
- Nedelec (alternative names: Ncurl)
Pyramid
The reference pyramid has vertices (0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 1, 0), and (0, 0, 1). Its sub-entities are numbered as follows.
List of supported elements
- Lagrange (alternative names: P)
Dual polygon
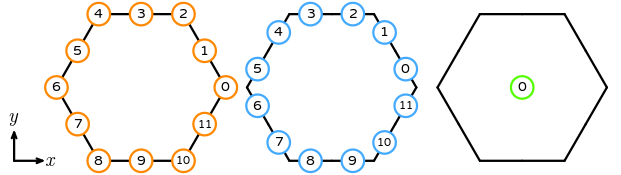
The reference dual polygon (hexagon example shown) has vertices (1, 0), (3/4, sqrt(3)/4), (1/2, sqrt(3)/2), (0, sqrt(3)/2), (-1/2, sqrt(3)/2), (-3/4, sqrt(3)/4), (-1, 0), (-3/4, -sqrt(3)/4), (-1/2, -sqrt(3)/2), (0, -sqrt(3)/2), (1/2, -sqrt(3)/2), and (3/4, -sqrt(3)/4). Its sub-entities are numbered as follows.
List of supported elements
- Buffa-Christiansen (alternative names: BC)
- dual polynomial (alternative names: dual P, dual)
- rotated Buffa-Christiansen (alternative names: RBC)
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file symfem-2025.12.0.tar.gz.
File metadata
- Download URL: symfem-2025.12.0.tar.gz
- Upload date:
- Size: 100.4 kB
- Tags: Source
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
d1adc109f930791c40894fa2ec3584d3ddaf6d5cf3b60d7dbf878ccca6301f13
|
|
| MD5 |
f68b5bfa85f1b09f272a8b6c38f81dc6
|
|
| BLAKE2b-256 |
c69ec2bf0f8a4c729bff41ef102ff07024ee1510629f5084209134affb8242a8
|
Provenance
The following attestation bundles were made for symfem-2025.12.0.tar.gz:
Publisher:
release.yml on mscroggs/symfem
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
symfem-2025.12.0.tar.gz -
Subject digest:
d1adc109f930791c40894fa2ec3584d3ddaf6d5cf3b60d7dbf878ccca6301f13 - Sigstore transparency entry: 756969830
- Sigstore integration time:
-
Permalink:
mscroggs/symfem@c37ffd6951a7fddd99353335fd5a511efdcf18fc -
Branch / Tag:
refs/heads/main - Owner: https://github.com/mscroggs
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
release.yml@c37ffd6951a7fddd99353335fd5a511efdcf18fc -
Trigger Event:
push
-
Statement type:
File details
Details for the file symfem-2025.12.0-py3-none-any.whl.
File metadata
- Download URL: symfem-2025.12.0-py3-none-any.whl
- Upload date:
- Size: 145.7 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/6.1.0 CPython/3.13.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
96ef58a11c0fcdfa6919b3be0560824030886a50819460e3291e3f784758206f
|
|
| MD5 |
8a7120abde65bddd2d0156613b79ed49
|
|
| BLAKE2b-256 |
9dbb308356225309cc60a59e8ddf826ce191a3916bd05cfaad3e36a428cad04b
|
Provenance
The following attestation bundles were made for symfem-2025.12.0-py3-none-any.whl:
Publisher:
release.yml on mscroggs/symfem
-
Statement:
-
Statement type:
https://in-toto.io/Statement/v1 -
Predicate type:
https://docs.pypi.org/attestations/publish/v1 -
Subject name:
symfem-2025.12.0-py3-none-any.whl -
Subject digest:
96ef58a11c0fcdfa6919b3be0560824030886a50819460e3291e3f784758206f - Sigstore transparency entry: 756969837
- Sigstore integration time:
-
Permalink:
mscroggs/symfem@c37ffd6951a7fddd99353335fd5a511efdcf18fc -
Branch / Tag:
refs/heads/main - Owner: https://github.com/mscroggs
-
Access:
public
-
Token Issuer:
https://token.actions.githubusercontent.com -
Runner Environment:
github-hosted -
Publication workflow:
release.yml@c37ffd6951a7fddd99353335fd5a511efdcf18fc -
Trigger Event:
push
-
Statement type: