a library for optimization on Riemannian manifolds
Project description
TensorFlow RiemOpt
A library for manifold-constrained optimization in TensorFlow.
Installation
To install the latest development version from GitHub:
pip install git+https://github.com/master/tensorflow-riemopt.git
To install a package from PyPI:
pip install tensorflow-riemopt
Features
The core package implements concepts in differential geometry, such as manifolds and Riemannian metrics with associated exponential and logarithmic maps, geodesics, retractions, and transports. For manifolds, where closed-form expressions are not available, the library provides numerical approximations.
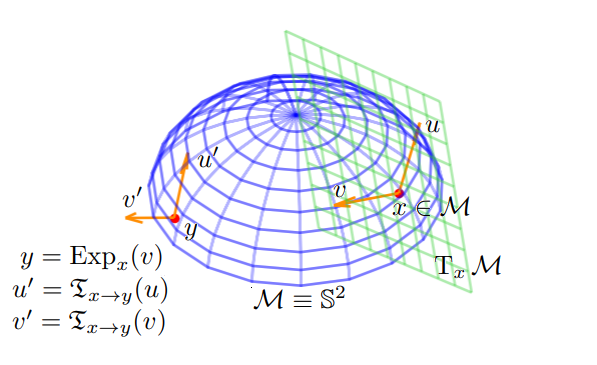
import tensorflow_riemopt as riemopt
S = riemopt.manifolds.Sphere()
x = S.projx(tf.constant([0.1, -0.1, 0.1]))
u = S.proju(x, tf.constant([1., 1., 1.]))
v = S.proju(x, tf.constant([-0.7, -1.4, 1.4]))
y = S.exp(x, v)
u_ = S.transp(x, y, u)
v_ = S.transp(x, y, v)
Manifolds
manifolds.Cholesky- manifold of lower triangular matrices with positive diagonal elementsmanifolds.Euclidian- unconstrained manifold with the Euclidean metricmanifolds.Grassmannian- manifold ofp-dimensional linear subspaces of then-dimensional spacemanifolds.Hyperboloid- manifold ofn-dimensional hyperbolic space embedded in then+1-dimensional Minkowski spacemanifolds.Poincare- the Poincaré ball model of the hyperbolic spacemanifolds.Product- Cartesian product of manifoldsmanifolds.SPDAffineInvariant- manifold of symmetric positive definite (SPD) matrices endowed with the affine-invariant metricmanifolds.SPDLogCholesky- SPD manifold with the Log-Cholesky metricmanifolds.SPDLogEuclidean- SPD manifold with the Log-Euclidean metricmanifolds.SpecialOrthogonal- manifold of rotation matricesmanifolds.Sphere- manifold of unit-normalized pointsmanifolds.StiefelEuclidean- manifold of orthonormalp-frames in then-dimensional space endowed with the Euclidean metricmanifolds.StiefelCanonical- Stiefel manifold with the canonical metricmanifolds.StiefelCayley- Stiefel manifold the retraction map via an iterative Cayley transform
Optimizers
Constrained optimization algorithms work as drop-in replacements for Keras optimizers for sparse and dense updates in both Eager and Graph modes.
optimizers.RiemannianSGD- Riemannian Gradient Descentoptimizers.RiemannianAdam- Riemannian Adam and AMSGradoptimizers.ConstrainedRMSProp- Constrained RMSProp
Layers
layers.ManifoldEmbedding- constrainedkeras.layers.Embeddinglayer
Examples
- ANTHEM - Choudhary, Nurendra, Nikhil Rao, Sumeet Katariya, Karthik Subbian, and Chandan K. Reddy. "ANTHEM: Attentive Hyperbolic Entity Model for Product Search." In Proceedings of the Fifteenth ACM International Conference on Web Search and Data Mining, 2022.
- SPDNet - Huang, Zhiwu, and Luc Van Gool. "A Riemannian network for SPD matrix learning." Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. AAAI Press, 2017.
- LieNet - Huang, Zhiwu, et al. "Deep learning on Lie groups for skeleton-based action recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.
- GrNet - Huang, Zhiwu, Jiqing Wu, and Luc Van Gool. "Building Deep Networks on Grassmann Manifolds." AAAI. AAAI Press, 2018.
- Hyperbolic Neural Network - Ganea, Octavian, Gary Bécigneul, and Thomas Hofmann. "Hyperbolic neural networks." Advances in neural information processing systems. 2018.
- Poincaré GloVe - Tifrea, Alexandru, Gary Becigneul, and Octavian-Eugen Ganea. "Poincaré Glove: Hyperbolic Word Embeddings." International Conference on Learning Representations. 2018.
References
If you find TensorFlow RiemOpt useful in your research, please cite:
@misc{smirnov2021tensorflow,
title={TensorFlow RiemOpt: a library for optimization on Riemannian manifolds},
author={Oleg Smirnov},
year={2021},
eprint={2105.13921},
archivePrefix={arXiv},
primaryClass={cs.MS}
}
Contact
For support or development inquiries, contact us at: tensorflow-riemopt-dev@googlegroups.com
Acknowledgment
TensorFlow RiemOpt was inspired by many similar projects:
- Manopt, a matlab toolbox for optimization on manifolds
- Pymanopt, a Python toolbox for optimization on manifolds
- Geoopt: Riemannian Optimization in PyTorch
- Geomstats, an open-source Python package for computations and statistics on nonlinear manifolds
License
The code is MIT-licensed.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file tensorflow_riemopt-0.3.1.tar.gz.
File metadata
- Download URL: tensorflow_riemopt-0.3.1.tar.gz
- Upload date:
- Size: 28.9 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.2.0 CPython/3.11.2
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
baff200d5b2968545455b2942a21649e6971f266600691bf8754df41611338ae
|
|
| MD5 |
3c1c3dc07720af648257ce9e5ace5a5a
|
|
| BLAKE2b-256 |
3a2f84fde6fd6d8d73a8b5237c174a5bad2b9dfb8640b6321dc32a0cafeb56b5
|


















