2D/3D serial and parallel triangular mesh generation for seismology
Project description
Create high-quality, simulation-ready 2D/3D meshes.
SeismicMesh: Triangular Mesh generation in Python
SeismicMesh is a Python package for simplex mesh generation in two or three dimensions. As an implementation of DistMesh, it produces high-geometric quality meshes at the expense of speed. For increased efficiency, the core package is written in C++, works in parallel, and uses the Computational Geometry Algorithms Library. SeismicMesh can also produce mesh-density functions from seismological data to be used in the mesh generator.
SeismicMesh is distributed under the GPL3 license and more details can be found in our short paper.
Table of contents
Installation
For installation, SeismicMesh needs CGAL:
sudo apt install libcgal-dev
After that, SeismicMesh can be installed from the Python Package Index (pypi), so with:
pip install -U SeismicMesh[io]
For more detailed information about installation and requirements see:
Install - How to install SeismicMesh.
Contributing
All contributions are welcome!
To contribute to the software:
- Fork the repository.
- Clone the forked repository, add your contributions and push the changes to your fork.
- Create a Pull request
Before creating the pull request, make sure that the tests pass by running
tox
Some things that will increase the chance that your pull request is accepted:
- Write tests.
- Add Python docstrings that follow the Sphinx.
- Write good commit and pull request messages.
Citing
You may use the following BibTeX entry:
@article{Roberts2021,
doi = {10.21105/joss.02687},
url = {https://doi.org/10.21105/joss.02687},
year = {2021},
publisher = {The Open Journal},
volume = {6},
number = {57},
pages = {2687},
author = {Keith J. Roberts and Rafael dos Santos Gioria and William J. Pringle},
title = {SeismicMesh: Triangular meshing for seismology},
journal = {Journal of Open Source Software}
}
Problems?
If something isn't working as it should or you'd like to recommend a new addition/feature to the software, please let me know by starting an issue through the issues tab. I'll try to get to it as soon as possible.
Examples
The user can quickly build quality 2D/3D meshes from seismic velocity models in serial/parallel.
BP2004
WARNING: To run the code snippet below you must download the 2D BP2004 seismic velocity model and then you must uncompress it (e.g., gunzip). This file can be downloaded from here
from mpi4py import MPI
import meshio
from SeismicMesh import get_sizing_function_from_segy, generate_mesh, Rectangle
comm = MPI.COMM_WORLD
"""
Build a mesh of the BP2004 benchmark velocity model in serial or parallel
Takes roughly 1 minute with 2 processors and less than 1 GB of RAM.
"""
# Name of SEG-Y file containg velocity model.
fname = "vel_z6.25m_x12.5m_exact.segy"
# Bounding box describing domain extents (corner coordinates)
bbox = (-12000.0, 0.0, 0.0, 67000.0)
# Desired minimum mesh size in domain
hmin = 75.0
rectangle = Rectangle(bbox)
# Construct mesh sizing object from velocity model
ef = get_sizing_function_from_segy(
fname,
bbox,
hmin=hmin,
wl=10,
freq=2,
dt=0.001,
grade=0.15,
domain_pad=1e3,
pad_style="edge",
)
points, cells = generate_mesh(domain=rectangle, edge_length=ef)
if comm.rank == 0:
# Write the mesh in a vtk format for visualization in ParaView
# NOTE: SeismicMesh outputs assumes the domain is (z,x) so for visualization
# in ParaView, we swap the axes so it appears as in the (x,z) plane.
meshio.write_points_cells(
"BP2004.vtk",
points[:, [1, 0]] / 1000,
[("triangle", cells)],
file_format="vtk",
)
EAGE
WARNING: To run the code snippet below you must download (and uncompress) the 3D EAGE seismic velocity model from (WARNING: File is ~500 MB) here
WARNING: Computationaly demanding! Running this example takes around 3 minutes in serial and requires around 2 GB of RAM due to the 3D nature of the problem and the domain size.
from mpi4py import MPI
import zipfile
import meshio
from SeismicMesh import (
get_sizing_function_from_segy,
generate_mesh,
sliver_removal,
Cube,
)
comm = MPI.COMM_WORLD
# Bounding box describing domain extents (corner coordinates)
bbox = (-4200.0, 0.0, 0.0, 13520.0, 0.0, 13520.0)
# Desired minimum mesh size in domain.
hmin = 150.0
# This file is in a big Endian binary format, so we must tell the program the shape of the velocity model.
path = "Salt_Model_3D/3-D_Salt_Model/VEL_GRIDS/"
if comm.rank == 0:
# Extract binary file Saltf@@ from SALTF.ZIP
zipfile.ZipFile(path + "SALTF.ZIP", "r").extract("Saltf@@", path=path)
fname = path + "Saltf@@"
# Dimensions of model (number of grid points in z, x, and y)
nx, ny, nz = 676, 676, 210
cube = Cube(bbox)
# A graded sizing function is created from the velocity model along with a signed distance function by passing
# the velocity grid that we created above.
# More details can be found here: https://seismicmesh.readthedocs.io/en/master/api.html
ef = get_sizing_function_from_segy(
fname,
bbox,
hmin=hmin,
dt=0.001,
freq=2,
wl=5,
grade=0.15,
hmax=5e3,
domain_pad=250,
pad_style="linear_ramp",
nz=nz,
nx=nx,
ny=ny,
byte_order="big",
axes_order=(2, 0, 1), # order for EAGE (x, y, z) to default order (z,x,y)
axes_order_sort="F", # binary is packed in a FORTRAN-style
)
points, cells = generate_mesh(domain=cube, edge_length=ef, max_iter=75)
# For 3D mesh generation, we provide an implementation to bound the minimum dihedral angle::
# We use the preserve kwarg to ensure the level-set is very accurately preserved.
points, cells = sliver_removal(
points=points, bbox=bbox, domain=cube, edge_length=ef, preserve=True
)
# Meshes can be written quickly to disk using meshio and visualized with ParaView::
if comm.rank == 0:
# NOTE: SeismicMesh outputs assumes the domain is (z,x,y) so for visualization
# in ParaView, we swap the axes so it appears as in the (x,y,z) plane.
meshio.write_points_cells(
"EAGE_Salt.vtk",
points[:, [1, 2, 0]] / 1000.0,
[("tetra", cells)],
)
The user can still specify their own signed distance functions and sizing functions to generate_mesh (in serial or parallel) just like the original DistMesh algorithm but now with quality bounds in 3D. Try the codes below!
Cylinder

# Mesh a cylinder
from mpi4py import MPI
import meshio
import SeismicMesh
comm = MPI.COMM_WORLD
hmin = 0.10
cylinder = SeismicMesh.Cylinder(h=1.0, r=0.5)
points, cells = SeismicMesh.generate_mesh(
domain=cylinder,
edge_length=hmin,
)
points, cells = SeismicMesh.sliver_removal(
points=points,
domain=cylinder,
edge_length=hmin,
)
if comm.rank == 0:
meshio.write_points_cells(
"Cylinder.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Disk
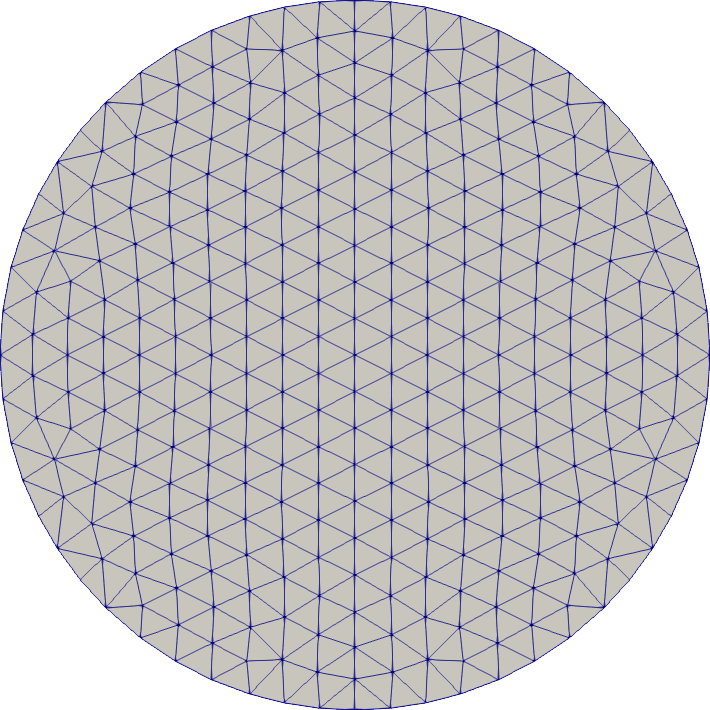
# mesh a disk
import meshio
import SeismicMesh
disk = SeismicMesh.Disk([0.0, 0.0], 1.0)
points, cells = SeismicMesh.generate_mesh(domain=disk, edge_length=0.1)
meshio.write_points_cells(
"disk.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Square

# mesh a square/rectangle
import meshio
import SeismicMesh
bbox = (0.0, 1.0, 0.0, 1.0)
square = SeismicMesh.Rectangle(bbox)
points, cells = SeismicMesh.generate_mesh(domain=square, edge_length=0.05)
meshio.write_points_cells(
"square.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Cube

# mesh a cuboid/cube
import meshio
import SeismicMesh
bbox = (0.0, 1.0, 0.0, 1.0, 0.0, 1.0)
cube = SeismicMesh.Cube(bbox)
points, cells = SeismicMesh.generate_mesh(domain=cube, edge_length=0.05)
points, cells = SeismicMesh.sliver_removal(points=points, domain=cube, edge_length=0.05)
meshio.write_points_cells(
"cube.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Torus

# mesh a torus
import meshio
import SeismicMesh
hmin = 0.10
torus = SeismicMesh.Torus(r1=1.0, r2=0.5)
points, cells = SeismicMesh.generate_mesh(
domain=torus,
edge_length=hmin,
)
points, cells = SeismicMesh.sliver_removal(
points=points, domain=torus, edge_length=hmin
)
meshio.write_points_cells(
"torus.vtk",
points,
[("tetra", cells)],
)
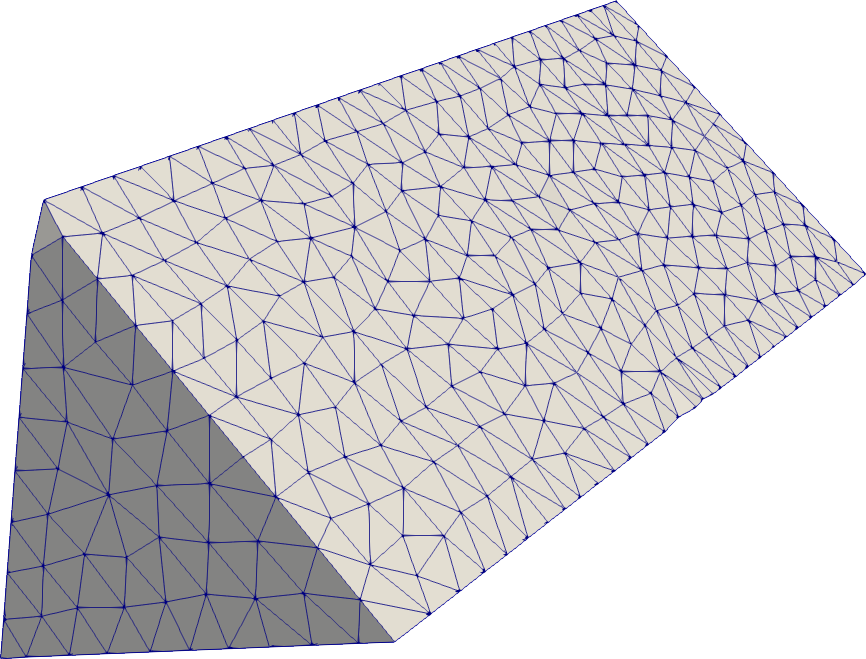
Prism
# mesh a prism
import meshio
import SeismicMesh
hmin = 0.05
prism = SeismicMesh.Prism(b=0.5, h=0.5)
points, cells = SeismicMesh.generate_mesh(
domain=prism,
edge_length=hmin,
)
points, cells = SeismicMesh.sliver_removal(
points=points, domain=prism, edge_length=hmin
)
meshio.write_points_cells(
"prism.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Union

# Compute the union of several SDFs to create more complex geometries
import meshio
import SeismicMesh
h = 0.10
rect0 = SeismicMesh.Rectangle((0.0, 1.0, 0.0, 0.5))
rect1 = SeismicMesh.Rectangle((0.0, 0.5, 0.0, 1.0))
disk0 = SeismicMesh.Disk([0.5, 0.5], 0.5)
union = SeismicMesh.Union([rect0, rect1, disk0])
# Visualize the signed distance function
union.show()
points, cells = SeismicMesh.generate_mesh(domain=union, edge_length=h)
meshio.write_points_cells(
"Lshape_wDisk.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Intersection
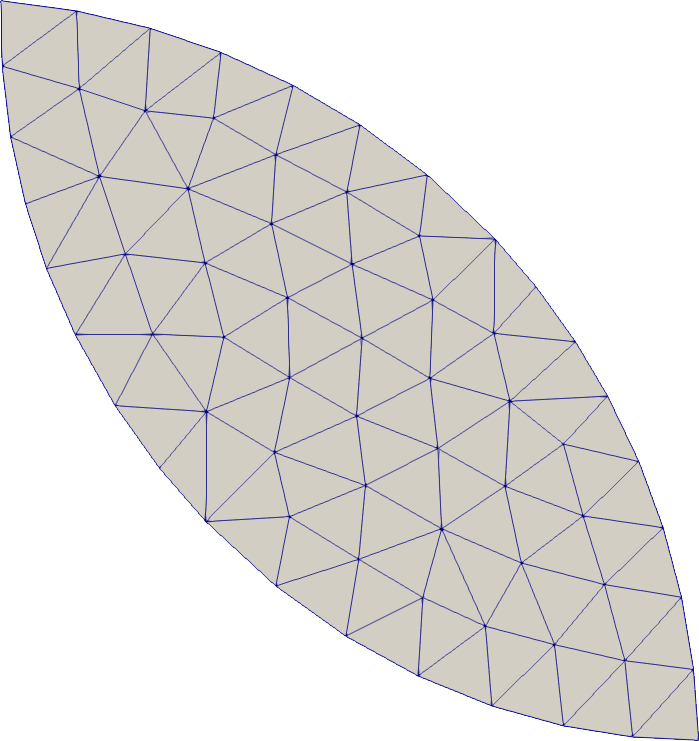
# Compute the intersection of several SDFs to create more complex geometries
import meshio
import SeismicMesh
h = 0.05
rect0 = SeismicMesh.Rectangle((0.0, 1.0, 0.0, 1.0))
disk0 = SeismicMesh.Disk([0.25, 0.25], 0.5)
disk1 = SeismicMesh.Disk([0.75, 0.75], 0.5)
intersection = SeismicMesh.Intersection([rect0, disk0, disk1])
points, cells = SeismicMesh.generate_mesh(domain=intersection, edge_length=h)
meshio.write_points_cells(
"Leaf.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Difference
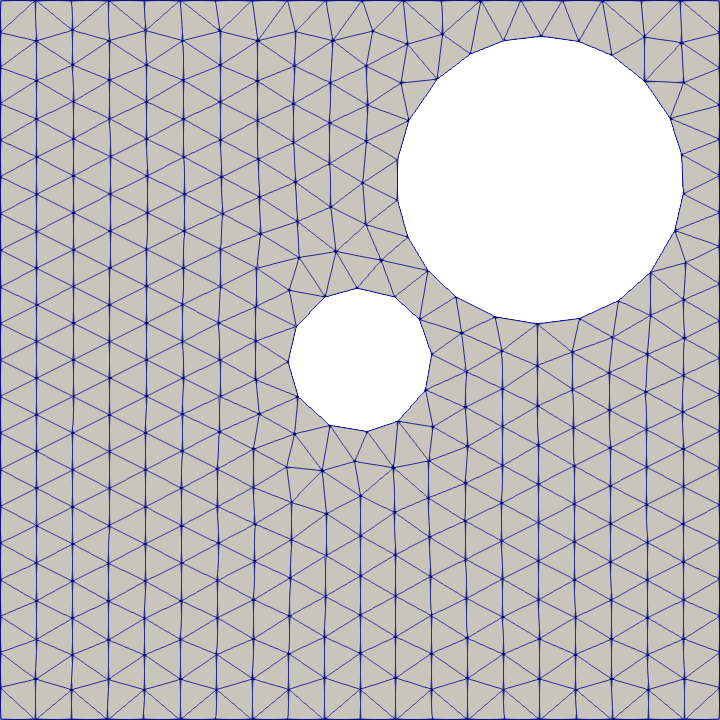
# Compute the difference of two SDFs to create more complex geometries.
import meshio
import SeismicMesh
h = 0.05
rect0 = SeismicMesh.Rectangle((0.0, 1.0, 0.0, 1.0))
disk0 = SeismicMesh.Disk([0.5, 0.5], 0.1)
disk1 = SeismicMesh.Disk([0.75, 0.75], 0.20)
difference = SeismicMesh.Difference([rect0, disk0, disk1])
points, cells = SeismicMesh.generate_mesh(domain=difference, edge_length=h)
meshio.write_points_cells(
"Hole.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Difference of Signed Distance Functions in 3-D

# Compute the difference of several SDFs in 3D
import meshio
import SeismicMesh
h = 0.10
cube0 = SeismicMesh.Cube((0.0, 1.0, 0.0, 1.0, 0.0, 1.0))
ball1 = SeismicMesh.Ball([0.5, 0.0, 0.5], 0.30)
ball2 = SeismicMesh.Ball([0.5, 0.5, 0.0], 0.30)
ball3 = SeismicMesh.Ball([0.0, 0.5, 0.5], 0.30)
ball4 = SeismicMesh.Ball([0.5, 0.5, 0.5], 0.45)
difference = SeismicMesh.Difference([cube0, ball1, ball2, ball3, ball4])
points, cells = SeismicMesh.generate_mesh(domain=difference, edge_length=h, verbose=1)
points, cells = SeismicMesh.sliver_removal(
points=points, domain=difference, edge_length=h, verbose=1
)
meshio.write_points_cells(
"Cube_wHoles.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Immersion

# Immerse a subdomain so that it's boundary is conforming in the mesh.
import numpy as np
import meshio
import SeismicMesh
box0 = SeismicMesh.Rectangle((-1.25, 0.0, -0.250, 1.250))
disk0 = SeismicMesh.Disk([-0.5, 0.5], 0.25)
hmin = 0.10
fh = lambda p: 0.05 * np.abs(disk0.eval(p)) + hmin
points, cells = SeismicMesh.generate_mesh(
domain=box0,
edge_length=fh,
h0=hmin,
subdomains=[disk0],
max_iter=100,
)
meshio.write_points_cells(
"Square_wsubdomain.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Boundaries
Boundary conditions can also be prescribed and written to gmsh compatible files using mehsio. In the following example, we immerse a disk into the connectivity and then prescribe boundary conditions around the circle and each wall of the domain for later usage inside a finite element solver.

import numpy as np
import meshio
import SeismicMesh as sm
bbox = (0.0, 10.0, 0.0, 1.0)
channel = sm.Rectangle(bbox)
suspension = sm.Disk([0.5, 0.5], 0.25)
hmin = 0.10
fh = lambda p: 0.05 * np.abs(suspension.eval(p)) + hmin
points, cells = sm.generate_mesh(
domain=channel,
edge_length=fh,
h0=hmin,
subdomains=[suspension],
max_iter=1000,
)
# This gets the edges of the mesh in a winding order (clockwise or counterclockwise).
ordered_bnde = sm.geometry.get_winded_boundary_edges(cells)
# We use the midpoint of the edge to determine its boundary label
mdpt = points[ordered_bnde].sum(1) / 2
infl = ordered_bnde[mdpt[:, 0] < 1e-6, :] # x=0.0
outfl = ordered_bnde[mdpt[:, 0] > 9.9 + 1e-6, :] # x=10.0
walls = ordered_bnde[
(mdpt[:, 1] < 1e-6) | (mdpt[:, 1] > 0.99 + 1e-6), :
] # y=0.0 or y=1.0
cells_prune = cells[suspension.eval(sm.geometry.get_centroids(points, cells)) < 0]
circle = sm.geometry.get_winded_boundary_edges(cells_prune)
# Write to gmsh22 format with boundary conditions for the walls and disk/circle.
meshio.write_points_cells(
"example.msh",
points,
cells=[
("triangle", cells),
("line", np.array(infl)),
("line", np.array(outfl)),
("line", np.array(walls)),
("line", np.array(circle)),
],
field_data={
"InFlow": np.array([11, 1]),
"OutFlow": np.array([12, 1]),
"Walls": np.array([13, 1]),
"Circle": np.array([14, 1]),
},
cell_data={
"gmsh:physical": [
np.repeat(3, len(cells)),
np.repeat(11, len(infl)),
np.repeat(12, len(outfl)),
np.repeat(13, len(walls)),
np.repeat(14, len(circle)),
],
"gmsh:geometrical": [
np.repeat(1, len(cells)),
np.repeat(1, len(infl)),
np.repeat(1, len(outfl)),
np.repeat(1, len(walls)),
np.repeat(1, len(circle)),
],
},
file_format="gmsh22",
binary=False,
)
Periodic

# Repeat primitives to create more complex domains/shapes.
import SeismicMesh
import meshio
hmin = 0.30
bbox = (0.0, 10.0, 0.0, 10.0, 0.0, 10.0)
torus = SeismicMesh.Torus(r1=1.0, r2=0.5)
# the Repeat function takes a list specifying the repetition period in each dim
periodic_torus = SeismicMesh.Repeat(bbox, torus, [2.0, 2.0, 2.0])
points, cells = SeismicMesh.generate_mesh(domain=periodic_torus, edge_length=hmin)
points, cells = SeismicMesh.sliver_removal(
points=points, domain=periodic_torus, edge_length=hmin
)
meshio.write_points_cells(
"periodic_torus.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Rotations

# Rotate squares in 2D
import numpy as np
import meshio
import SeismicMesh
bbox = (0.0, 1.0, 0.0, 1.0)
rotations = np.linspace(-3.14, 3.14, 40)
squares = []
for _, rotate in enumerate(rotations):
squares.append(SeismicMesh.Rectangle(bbox, rotate=rotate))
rotated_squares = SeismicMesh.Union(squares)
points, cells = SeismicMesh.generate_mesh(domain=rotated_squares, edge_length=0.05)
meshio.write_points_cells(
"rotated_squares" + str(rotate) + ".vtk",
points,
[("triangle", cells)],
file_format="vtk",
)

# Same as above but for cubes
import numpy as np
import meshio
import SeismicMesh
bbox = (0.0, 1.0, 0.0, 1.0, 0.0, 1.0)
rotations = np.linspace(-3.14, 3.14, 40)
cubes = []
for _, rotate in enumerate(rotations):
cubes.append(SeismicMesh.Cube(bbox, rotate=rotate))
rotated_cubes = SeismicMesh.Union(cubes)
points, cells = SeismicMesh.generate_mesh(domain=rotated_cubes, edge_length=0.10)
meshio.write_points_cells(
"rotated_cubes.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Stretching
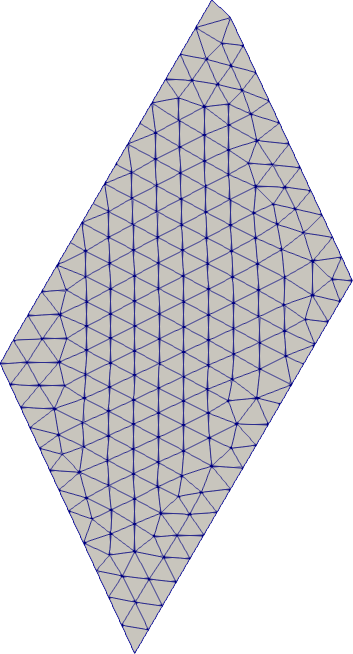
# Geometric primitives can be stretched (while being rotated)
import meshio
from SeismicMesh import *
domain = Rectangle((0.0, 1.0, 0.0, 1.0), stretch=[0.5, 2.0], rotate=0.1*3.14)
points, cells = generate_mesh(domain=domain, edge_length=0.1, verbose=2)
meshio.write_points_cells(
"stretched_square.vtk",
points,
[("triangle", cells)],
file_format="vtk",
)
Translation

# Geometric primitives can be translated (while being rotated and stretched)
import meshio
from SeismicMesh import *
cuboid = Cube(
(0.0, 1.0, 0.0, 1.0, 0.1, 1.0),
stretch=[1.5, 1.5, 1.5],
translate=[0.5, 4.0, 1.0],
rotate=4.5 * 3.14,
)
points, cells = generate_mesh(domain=cuboid, edge_length=0.10, max_iter=200)
points, cells = sliver_removal(points=points, domain=cuboid, edge_length=0.10, preserve=True)
meshio.write_points_cells(
"stretched_square.vtk",
points,
[("tetra", cells)],
file_format="vtk",
)
Checking
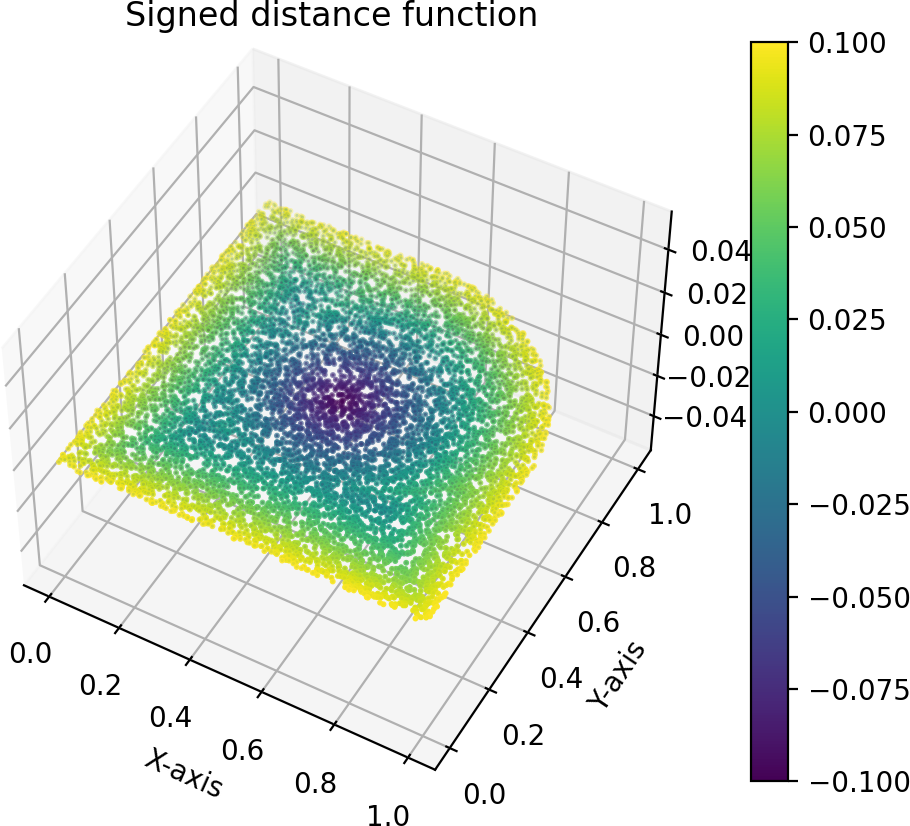
SeismicMesh's mesh generator is sensitive to poor geometry definitions and thus you should probably check it prior to complex expensive meshing. We enable all signed distance functions to be visualized via the domain.show() method where domain is an instance of a signed distance function primitive from SeismicMesh.geometry. Note: you can increase the number of samples to visualize the signed distance function by increasing the kwarg samples to the show method, which is by default set to 10000.
Parallelism
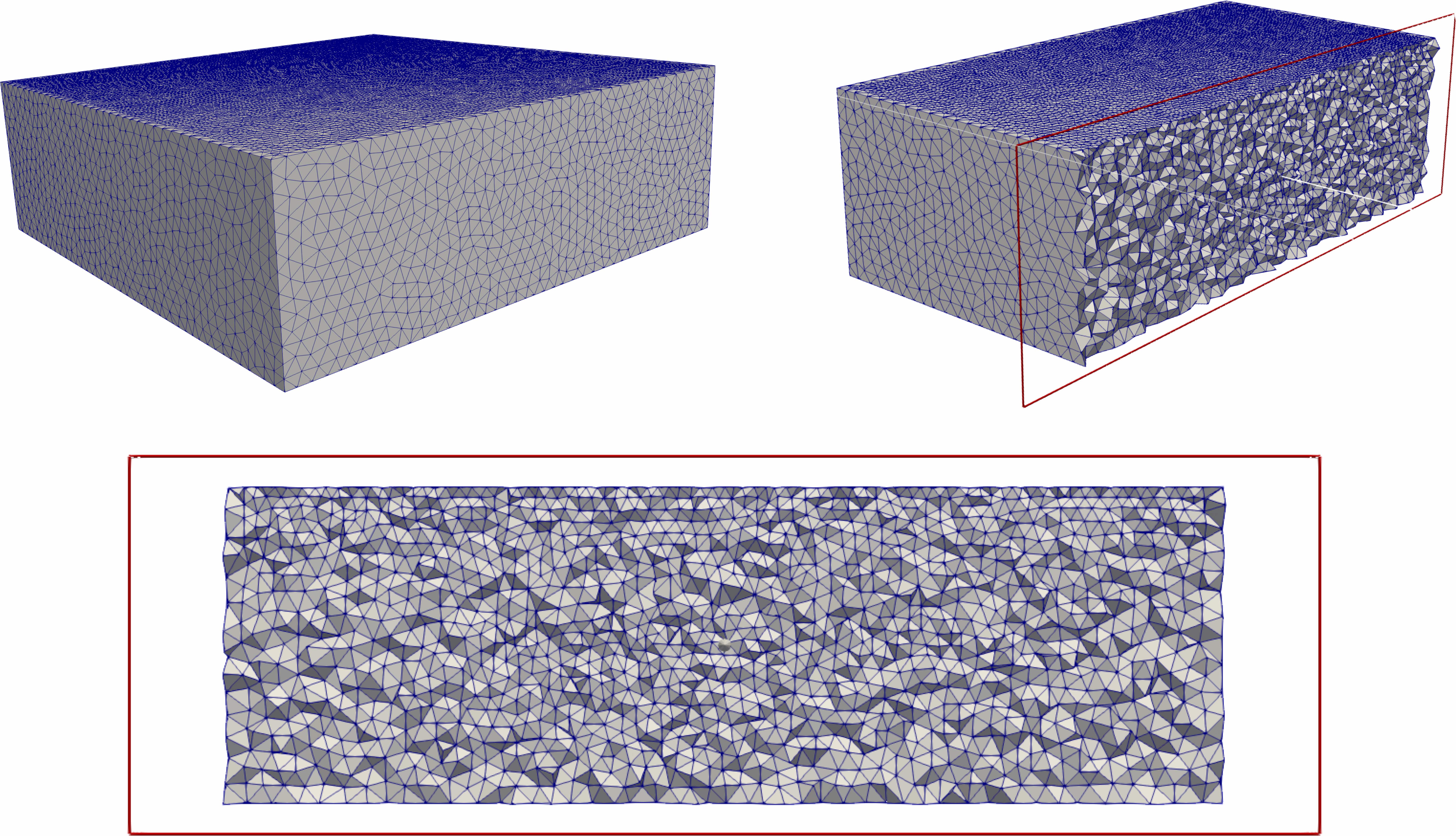
A simplified version of the parallel Delaunay algorithm proposed by Peterka et. al 2014 is implemented inside the DistMesh algorithm, which does not consider sophisticated domain decomposition or load balancing yet. A peak speed-up of approximately 6 times using 11 cores when performing 50 meshing iterations is observed to generate the 33M cell mesh of the EAGE P-wave velocity model. Parallel performance in 2D is better with peak speedups around 8 times using 11 cores. While the parallel performance is not perfect at this stage of development, the capability reduces the generation time of this relatively large example (e.g., 33 M cells) from 91.0 minutes to approximately 15.6 minutes. Results indicate that the simple domain decomposition approach inhibit perfect scalability. The machine used for this experiment was an Intel Xeon Gold 6148 machine clocked at 2.4 GHz with 192 GB of RAM connected together with a 100 Gb/s InfiniBand network.
To use parallelism see the docs
See the paper/paper.md and associated figures for more details.
Performance
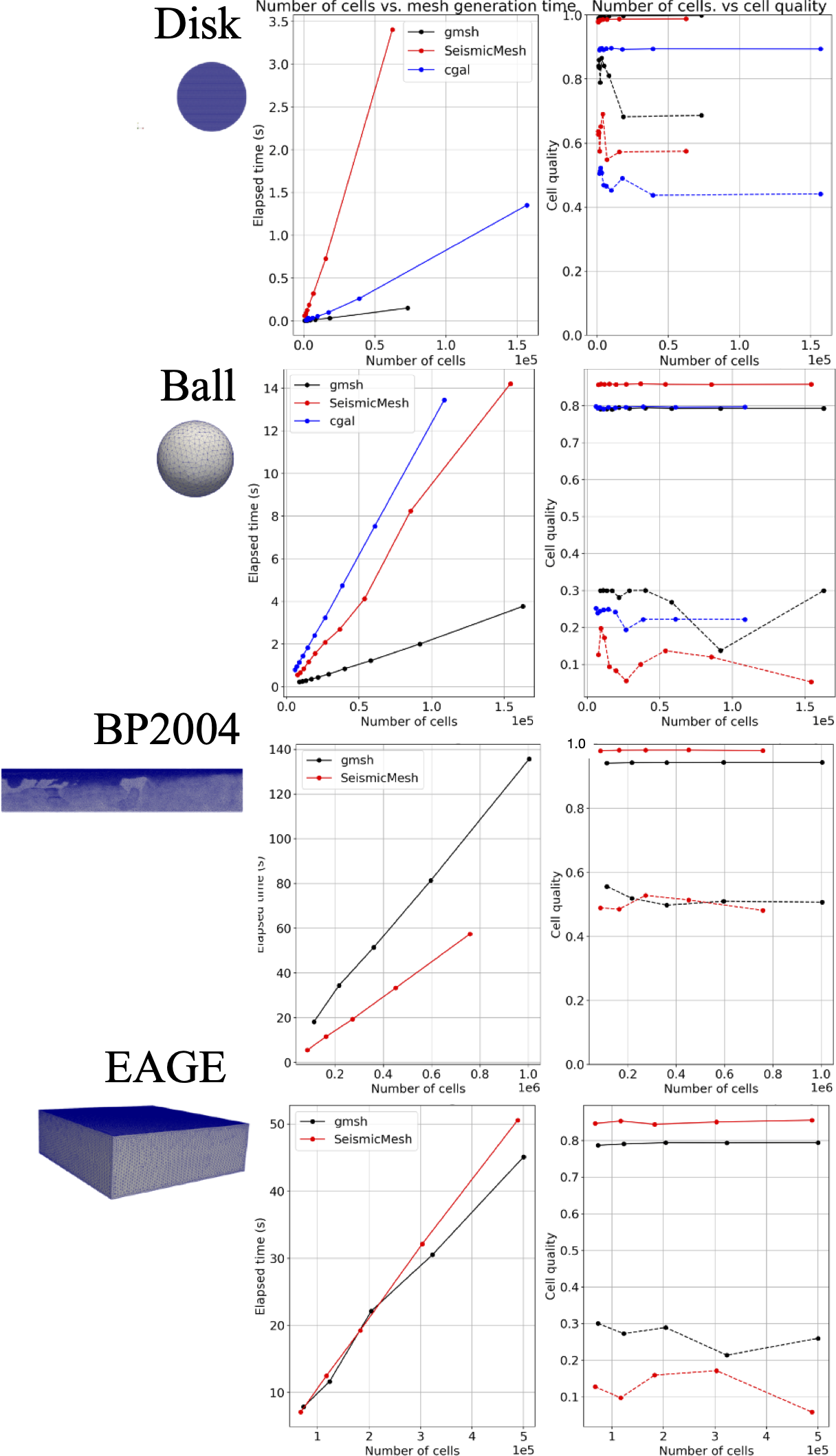
**How does performance and cell quality compare to Gmsh and CGAL mesh generators?
Here we use SeismicMesh 3.1.4, pygalmesh 0.8.2, and pygmsh 7.0.0 (more details in the benchmarks folder).
Some key findings:
- Mesh generation in 2D and 3D using analytical sizing functions is quickest when using Gmsh but a closer competition for CGAL and SeismicMesh.
- However, using mesh sizing functions defined on gridded interpolants significantly slow down both Gmsh and CGAL. In these cases, SeismicMesh and Gmsh perform similarly both outperforming CGAL's 3D mesh generator in terms of mesh generation time.
- All methods produce 3D triangulations that have a minimum dihedral angle > 10 degrees enabling stable numerical simulation (not shown)
- Head over to the
benchmarksfolder for more detailed information on these experiments.
-
In the figure for the panels that show cell quality, solid lines indicate the mean and dashed lines indicate the minimum cell quality in the mesh.
-
Note: it's important to point out here that a significant speed-up can be achieved for moderate to large problems using the parallel capabilities provided in SeismicMesh.
**For an additional comparison of SeismicMesh against several other popular mesh generators head over to meshgen-comparison.
Changelog
The format is based on Keep a Changelog, and this project adheres to Semantic Versioning.
Unrelease
- None
[3.6.1]-2021-05-22
Added
- Smoothed sets (e.g., intersections, differences, and unions)
- Conversion of velocity data from feet-second to meters-second
- Support for fixed points in iterative Laplacian mesh smoother.
Improved
- Simplified pybind11 build system.
- Now using pytest-codeblocks instead of exdown
[3.5.0]-2021-03-09
Added
- Rotations for all geometric primitives
- Stretching for all geometric primitives
- Visuzlization of signed distance functions
Fixed
- Support for Python 3.9
Improved
- Fixed points in iterative Laplacian smooth
[3.4.0]-2021-02-14
Added
- Mesh improvement now solves Lapl. smoothing as a fixed-point problem using AMG solver.
- User can now mesh user-defined sizing functions in parallel (not from :class:SizeFunction)
- Ability to specify data type
dtypeof floating point number inside binary files. - Example how to specify and write boundary conditions.
Improved
- Faster unique edge calculation.
[3.3.0]-2021-01-08
Added
- Ability to improve accuracy of level-set when performing 3d sliver removal.
Improved
- Marginally faster parallel speedup at scale in 2d/3d
[3.2.0] -2020-12-14
Added
- Adding basic periodic domains with the
RepeatSDF. sliver_removalhas optional variable step size when perturbing vertices. Helps to remove the "last sliver".
Improved
- Faster rectangle and cube primitives.
- Reworking CPP code and bottlenecks...20-30% faster
generate_meshin parallel for 2D/3D from previous versions.
[3.1.7] - 2020-11-27
Improved
- Table of contents in README
Added
- More testing of sliver removal and 2d mesh generation qualities.
Fixed
- Disabled bug when doing Newton boundary projection at the end of 3d
sliver_removal.
[3.1.6] - 2020-11-26
Bug present with sliver removal. Recommend to not use.
Added
- Unit testing three versions of Python (3.6.1, 3.7.4, 3.8.1)
[3.1.5] - 2020-11-24
- Support for constraining/immersing subdomains represented as signed distance functions.
- Faster cell manipulation operations for ~5-10% better speedups in parallel.
- Projection of points back onto level set.
[3.1.4] - 2020-11-15
- Laplacian smoothing at termination for 2D meshing...significantly improves minimum cell quality.
- Made
hmina field of the SizeFunction class, which implies the user no longer needs to passh0togenerate_meshorsliver_removal.
[3.1.3] - 2020-11-06
Fixed
- Cylinder radius and height are now correct.
- Torus, Prism, and Cylinder now have
dimtag.
Improved
- More control over the
gradoption in the mesh sizing function.
[3.1.2] - 2020-11-04
Improved
- Faster calculation of boundary vertices.
- More robust sliver removal in 3D.
Fixed
- Corners are only constrained for constant resolution meshes
[3.1.0] - 2020-10-28
Added
- New geometric primitives--torus, wedge/prism, and cylinder.
- Updated images on README.
Fixed
- Only constrain corners near 0-level set.
- Bug fix to 3D binary velocity reading.
[3.0.6] - 2020-10-21
Fixed
- Silence messages about pfix when verbose=0
Added
- Added more examples on README
- New unions/intersections/differences with several SDF primivitives
- Automatic corner constraints in serial
[3.0.5] - 2020-10-18
Fixed
- Preserving fixed points in serial.
- Units in km-s detection warning bug.
- Docstring fixes to
generate_mesh - Improved mesh quality in 3D
Added
- Automatic corner point extraction for cubes and rectangles.
- More support for reading binary files packed in a binary format.
- Check to make sure bbox is composed of all floats.
[3.0.4] - 2020-10-12
Added
- Improve conformity of level-set in final mesh through additional set of Newton boundary projection iterations.
More information
All other information is available at: https://seismicmesh.readthedocs.io
Getting started - Learn the basics about the program and the application domain.
Tutorials - Tutorials that will guide you through the main features.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file SeismicMesh-3.6.2.tar.gz.
File metadata
- Download URL: SeismicMesh-3.6.2.tar.gz
- Upload date:
- Size: 20.5 MB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.4.1 importlib_metadata/4.0.1 pkginfo/1.7.0 requests/2.25.1 requests-toolbelt/0.9.1 tqdm/4.61.0 CPython/3.7.4
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
476cc4a5b3464f110dc28d0f10975a53d86428ab7debd7e6ba7613c7dfd9c66a
|
|
| MD5 |
d08bab15320a4ffbcd7461cf687f2a8f
|
|
| BLAKE2b-256 |
8cde3df9b9c68080bf1800fccce118a9ca94bd46a15c886dd62062128847d72e
|
File details
Details for the file SeismicMesh-3.6.2-cp37-cp37m-macosx_10_14_x86_64.whl.
File metadata
- Download URL: SeismicMesh-3.6.2-cp37-cp37m-macosx_10_14_x86_64.whl
- Upload date:
- Size: 774.1 kB
- Tags: CPython 3.7m, macOS 10.14+ x86-64
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.4.1 importlib_metadata/4.0.1 pkginfo/1.7.0 requests/2.25.1 requests-toolbelt/0.9.1 tqdm/4.61.0 CPython/3.7.4
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
179976c06cf6ccbe55e6e0111d444877d1982189dd22c601b3e8cf6937daf12c
|
|
| MD5 |
2b6138d16b974506119f025838c090e6
|
|
| BLAKE2b-256 |
a0a7d8f5d12087859bd7d1d247d8eae4a3216fd4606e82c5ebff0780d448b8ce
|